算術演算
メモ
以下の節は、どのデータ型とスケーリングを選択するとオーバーフローや精度の低下が発生するかを理解するのに役立ちます。
モジュロ演算
2 進数はモジュロ演算に基づきます。モジュロ演算は有限数値セットのみを使用して、そのセットの範囲に収まらない計算結果をラップしてセット内に戻します。
たとえば、日常的な時計はモジュロ 12 演算を使用しています。このシステムの数字は 1 ~ 12 のみです。そのため、"時計" システムで 9 足す 9 は 6 です。これは数値円として容易に可視化できます。

同様に、2 進数では 0 と 1 しか使用できないので、この範囲外となる演算結果は "円を周って" 0 または 1 にラップされます。
2 の補数
2 の補数は符号付き固定小数点数を表す一般的な方法です。2 の補数では、正の数値が常に 0 から始まり、負の数値が常に 1 から始まります。2 の補数の最初のビットが 0 の場合、値は標準的な 2 進数の値を計算して得られます。2 の補数の最初のビットが 1 の場合、値は左端のビットが負であると想定し、2 進数の値を計算して得られます。以下に例を示します。
2 の補数を使用して負の 2 進数を計算するには、次のようにします。
1 の補数を取ります。つまり、0 はすべて 1 に反転し、1 はすべて 0 に反転します。
2 進数を使用して 1 を足します。
元の語長を超えたビットはすべて破棄します。
たとえば、11010 (-6) の負を取ることにします。まず、この数値の 1 の補数を取るか、次のようにビットを反転します。
次に、1 を足してすべての数値を 0 か 1 にラップします。
加算と減算
固定小数点数の加算では、加数の 2 進小数点を整列する必要があります。次に、0 または 1 以外の数値が使用されないように、2 進数を使用して加算を実行します。
たとえば、010010.1 (18.5) と 0110.110 (6.75) の加算は次のようになります。
固定小数点の減算は加算と同じですが、負の値に 2 の補数を使用します。減算では、加数を符号拡張して相互の長さをマッチさせなければなりません。たとえば、010010.1 (18.5) から 0110.110 (6.75) を減算します。

加算を実行する大部分の固定小数点 DSP System Toolbox™ ブロックは、加算を行う前に加算器入力をアキュムレータのデータ型にキャストします。したがって、加算中に 2 進小数点を揃えるためのシフトは不要です。詳細については、キャストを参照してください。
乗算
2 の補数固定小数点数の乗算は通常の 10 進法の乗算と類似していますが、中間結果を加算する前に符号拡張を行って左側を揃えなければならない点が異なります。
たとえば、10.11 (-1.25) と 011 (3) の乗算は次のようになります。

乗算のデータ型
以下の図に、システム ツールボックス ソフトウェアで固定小数点の乗算に使用されるデータ型を示します。これらの図は、実数と実数、複素数と実数、複素数と複素数の乗算に使用されるデータ型の違いを説明しています。特定のブロックが複素数の固定小数点入力を受け入れるかどうかを判断するには、そのブロックのリファレンス ページを参照してください。
多くの場合、乗算の実行中に使用されるデータ型をブロック マスクで設定できます。詳細については、キャストを参照してください。
メモ
以下の図は、システム ツールボックス ソフトウェアでの乗算における固定小数点データ型の使用を示すものです。ソフトウェアで乗算の実行に使用される実際のサブシステムを表すものではありません。
実数と実数の乗算. 次の図は、2 つの実数の乗算でシステム ツールボックス ソフトウェアが使用するデータ型を示します。下の図に示すように、ソフトウェアはこの演算の出力を乗算器出力データ型で返します。

実数と複素数の乗算. 次の図は、実数と複素数の固定小数点数の乗算でシステム ツールボックス ソフトウェアが使用するデータ型を示します。実数と複素数の乗算と複素数と実数の乗算は等価です。下の図に示すように、ソフトウェアはこの演算の出力を乗算器出力データ型で返します。

複素数と複素数の乗算. 次の図は、システム ツールボックス ソフトウェアで行われる 2 つの複素数固定小数点数の乗算を示します。図からわかるように、ソフトウェアはこの演算の出力をアキュムレータの出力データ型で返す点に注意してください。

システム ツールボックスのブロックは加算や減算を実行する前に、アキュムレータのデータ型へのキャストを行います。前の図では、これは以下の C コードに相当します。
acc=ac; acc-=bd;
上記は減算器の場合です。
acc=ad; acc+=bc;
これは加算器の場合で、acc はアキュムレータです。
キャスト
算術演算を実行する多くの固定小数点のシステム ツールボックス ブロックで、必要に応じてアキュムレータ、中間の乗算および乗算器出力データ型や、ブロックの出力データ型を指定することが可能です。この節では、選択したデータ型によって符号拡張、ゼロ パディング、丸め、オーバーフローなどの処理が呼び出されるかどうかを判断できるよう、これらのデータ型へのキャストの概要を説明します。符号拡張とは、最上位ビットの値をもつビットを 2 の補数の最上部に追加することです。符号拡張では 2 進数の値は変更されません。パディングとは、バイナリ ワードの最下位ビットに 1 つ以上のゼロを付けて拡張することです。
アキュムレータのデータ型へのキャスト
加算または減算を実行する大部分の固定小数点システム ツールボックス ブロックでは、まずオペランドがアキュムレータのデータ型にキャストされます。多くの場合、ブロック マスクでアキュムレータのデータ型を指定できます。詳細については、ブロックの固定小数点属性の指定 (DSP System Toolbox)のアキュムレータのデータ型パラメーターに関する説明を参照してください。加数は加算される前にどちらも同じアキュムレータのデータ型にキャストされるため、2 進小数点を揃えるための追加のシフトは必要ありません。加算の結果はアキュムレータのデータ型のままであるため、オーバーフローが生じる可能性があります。
中間の乗算器データ型または乗算器出力データ型へのキャスト
乗算を実行するシステム ツールボックス ブロックでは、乗算器の出力が乗算器出力データ型に配置されます。その後で乗算器出力を乗算器に戻すブロックの場合、これをまず中間の乗算器データ型にキャストすることがあります。多くの場合、これらのデータ型はブロック マスクで指定できます。詳細については、ブロックの固定小数点属性の指定 (DSP System Toolbox)の中間の乗算器のデータ型パラメーターと乗算出力のデータ型パラメーターに関する説明を参照してください。
出力データ型へのキャスト
多くの固定小数点システム ツールボックス ブロックでは、ブロック出力のデータ型とスケーリングをマスクで指定できます。ソフトウェアでは、ブロックの入力端子と出力端子で型を混合することは許可されません。したがって、固定小数点データ型をサポートするシステム ツールボックス ブロックに固定小数点の出力データ型とスケーリングを指定する場合、そのブロックの入力端子に固定小数点信号を渡さなければなりません。固定小数点システム ツールボックス ブロックによる最後のキャストは、ブロックの出力データ型へのキャストです。
ブロックの入力端子と出力端子で固定小数点と浮動小数点の信号を混合することはできませんが、固定小数点信号をサポートするブロックの端子で語長と小数部の長さが異なる固定小数点信号を使用することは可能です。
キャストの例
中間のデータ型および特定のブロックで許可されるその他すべての中間の固定小数点データ型を選択する際は、各キャストによって受ける影響を考慮することが重要です。選択したデータ型によっては、オーバーフローや丸めが生じる可能性があります。次の 2 つの例は、オーバーフローと丸めが発生する状況を示しています。
短いデータ型から長いデータ型へのキャスト. 小数部が 2 ビットの 4 ビット データ型から、小数部が 7 ビットの 8 ビット データ型への非ゼロ数値のキャストについて考えてみます。
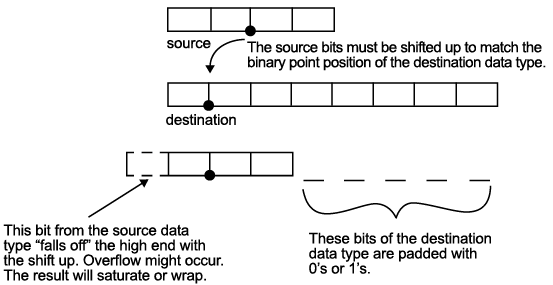
図のように、2 進小数点がキャスト先の 2 進小数点の位置とマッチするように、ソース ビットが左にシフトします。最上位のソース ビットがあふれるため、オーバーフローが発生する可能性があり、結果は飽和またはラップします。キャスト先データ型の末端にある空のビットは 0 または 1 で埋められます。
オーバーフローが発生しない場合は、空のビットが 0 で埋められます。
ラップが発生した場合は、空のビットが 0 で埋められます。
飽和が発生した場合は、以下の処理が行われます。
正の数値の空のビットは 1 で埋められます。
負の数値の空のビットは 0 で埋められます。
短いデータ型から長いデータ型へのキャストでもオーバーフローが発生する可能性があることがわかります。これは、ソース データ型の整数の長さ (ここでは 2) が、キャスト先データ型 (ここでは 1) の整数の長さより長いときに起こることがあります。同様に、短いデータ型から長いデータ型へのキャストでも、キャスト先のデータ型とスケーリングの小数ビット数がソースよりも少ない場合は、丸めが必要になることがあります。
長いデータ型から短いデータ型へのキャスト. 小数部が 7 ビットの 8 ビット データ型から、小数部が 2 ビットの 4 ビット データ型への非ゼロ数値のキャストについて考えてみます。

図のように、2 進小数点がキャスト先の 2 進小数点の位置とマッチするように、ソース ビットが右にシフトします。最上位ビットの値はソースにないため、この結果はキャスト先データ型の整数部を埋めるために拡張された符号になります。ソースの下位 5 ビットはキャスト先の小数部の長さに収まりません。したがって、結果は丸められるので精度が低下する可能性があります。
この場合は、長いデータ型から短いデータ型へのキャストでも、すべての整数ビットが維持されます。一方、短いデータ型にキャストする場合でも、キャスト先データ型の小数部の長さがソース データ型の小数部の長さ以上の場合は、完全精度を維持できます。ただし、その場合は結果の最上位からビットが失われ、オーバーフローが発生する可能性があります。
最悪の状況は、キャスト先データ型の整数の長さと小数部の長さが、ソースのデータ型とスケーリングの整数の長さと小数部の長さよりも短い場合に発生します。その場合は、オーバーフローと精度低下の両方が起こる可能性があります。