legendreP

ルジャンドル多項式

構文

legendreP(n,x)

説明

legendreP(n,x) は、x における n 次のルジャンドル多項式を返します。

例

数値入力およびシンボリック入力のルジャンドル多項式を求める

5.6 における 3 次のルジャンドル多項式を求めます。

legendreP(3,5.6)

ans =
  430.6400

x における 2 次のルジャンドル多項式を求めます。

syms x
legendreP(2,x)

ans =
(3*x^2)/2 - 1/2

n の数値を指定しない場合、関数 legendreP は多項式の陽的な式を求めることができず、関数呼び出しを返します。

syms n
legendreP(n,x)

ans =
legendreP(n, x)

ベクトル入力および行列入力によりルジャンドル多項式を求める

n = [1 2] と設定することにより 1 次および 2 次のルジャンドル多項式を求めます。

syms x
legendreP([1 2],x)

ans =
[ x, (3*x^2)/2 - 1/2]

legendreP は n の要素ごとに働き、2 つの要素をもつベクトルを返します。

複数の入力がベクトル、行列または多次元配列として指定されている場合、これらの入力は同じサイズでなければなりません。入力引数 n および x が行列である場合のルジャンドル多項式を求めます。

n = [2 3; 1 2];
xM = [x^2 11/7; -3.2 -x];
legendreP(n,xM)

ans =
[ (3*x^4)/2 - 1/2,        2519/343]
[           -16/5, (3*x^2)/2 - 1/2]

legendreP は n および x の要素ごとに働き、n および x と同じサイズの行列を返します。

ルジャンドル多項式を微分して極限を求める

limit を使用して、x が無限大傾向をもつ場合の 3 次のルジャンドル多項式の範囲を求めます。

syms x
expr = legendreP(4,x);
limit(expr,x,-Inf)

ans =
Inf

diff を使用して、5 次のルジャンドル多項式の 3 次導関数を求めます。

syms n
expr = legendreP(5,x);
diff(expr,x,3)

ans =
(945*x^2)/2 - 105/2

ルジャンドル多項式のテイラー級数展開を求める

taylor を使用して、x = 0 における 2 次のルジャンドル多項式のテイラー級数展開を求めます。

syms x
expr = legendreP(2,x);
taylor(expr,x)

ans =
(3*x^2)/2 - 1/2

ルジャンドル多項式のプロット

1 次から 4 次のルジャンドル多項式をプロットします。

syms x y
fplot(legendreP(1:4, x))
axis([-1.5 1.5 -1 1])
grid on

ylabel('P_n(x)')
title('Legendre polynomials of degrees 1 through 4')
legend('1','2','3','4','Location','best')

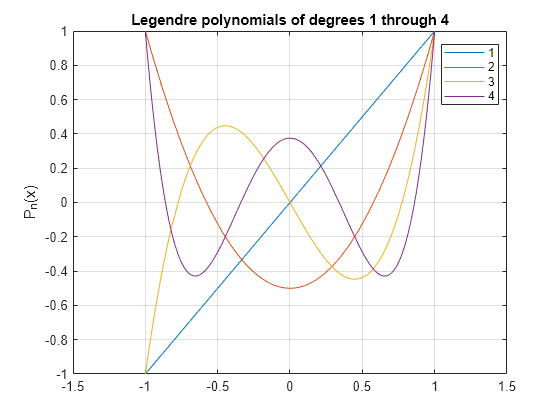
ルジャンドル多項式の根を求める

vpasolve を使用して、7 次のルジャンドル多項式の根を求めます。

syms x
roots = vpasolve(legendreP(7,x) == 0)

roots =
 -0.94910791234275852452618968404785
 -0.74153118559939443986386477328079
 -0.40584515137739716690660641207696
                                   0
  0.40584515137739716690660641207696
  0.74153118559939443986386477328079
  0.94910791234275852452618968404785

入力引数

n — 多項式の次数

非負の数値 | ベクトル | 行列 | 多次元配列 | シンボリック数 | シンボリック ベクトル | シンボリック行列 | シンボリック関数 | シンボリック多次元配列

多項式の次数。非負の数値、ベクトル、行列、多次元配列、あるいはシンボリック数、ベクトル、行列、関数または多次元配列として指定します。非スカラー入力のすべての要素は非負の整数またはシンボルでなければなりません。

x — 入力

数値 | ベクトル | 行列 | 多次元配列 | シンボリック数 | シンボリック ベクトル | シンボリック行列 | シンボリック関数 | シンボリック多次元配列

入力。数値、ベクトル、行列、多次元配列、あるいはシンボリック数、ベクトル、行列、関数または多次元配列として指定します。

詳細

ルジャンドル多項式

• ルジャンドル多項式は次のように定義されます。

  $$P\left(n,x\right)=\frac{1}{2^{n}n!}\frac{d^n}{d{x}^n}{\left(x^2-1\right)}^n.$$

• ルジャンドル多項式は次の再帰式を満たします。

  $$\begin{array}{l}P\left(n,x\right)=\frac{2n-1}{n}xP\left(n-1,x\right)-\frac{n-1}{n}P\left(n-2,x\right),\\ \text{where}\\ P\left(0,x\right)=1\\ P\left(1,x\right)=x.\end{array}$$

• ルジャンドル多項式は区間 [-1,1] において重み関数 w(x) = 1 と直交します。ここで、

  $${\displaystyle \underset{x=-1}{\overset{x=1}{\int }}P(n,x)P(m,x)dx}=\{\begin{array}{cc}0& \text{if }n\ne m\\ \frac{1}{n+1/2}& \text{if }n=m.\end{array}$$

• ゲーゲンバウアー多項式 G(n,a,x) との関係は次のとおりです。

  $$P\left(n,x\right)=G\left(n,\frac{1}{2},x\right).$$

• ヤコビ多項式 P(n,a,b,x) との関係は次のとおりです。

  $$P\left(n,x\right)=P\left(n,0,0,x\right).$$

バージョン履歴

R2014b で導入

参考

chebyshevT | chebyshevU | gegenbauerC | hermiteH | hypergeom | jacobiP | laguerreL