laguerreL

一般化ラゲール関数とラゲール多項式

構文

laguerreL(n,x)

laguerreL(n,a,x)

説明

laguerreL(n,x) は、n が非負の整数である場合は n 次のラゲール多項式を返します。n が非負の整数でない場合は laguerreL はラゲール関数を返します。詳細については、一般化ラゲール関数を参照してください。

laguerreL(n,a,x) は、n が非負の整数である場合は n 次の一般化ラゲール多項式を返します。n が非負の整数でない場合、laguerreL は一般化ラゲール関数を返します。

例

数値入力およびシンボリック入力のラゲール多項式を求める

入力 4.3 に対する 3 次のラゲール多項式を求めます。

laguerreL(3,4.3)

ans =
    2.5838

シンボリック入力のラゲール多項式を求めます。次数 n を 3 に指定して、陽的な多項式を返すようにします。

syms x
laguerreL(3,x)

ans =
- x^3/6 + (3*x^2)/2 - 3*x + 1

ラゲール多項式の次数 n が指定されていない場合、laguerreL は多項式を求めることはできません。laguerreL が多項式を求めることができない場合、関数呼び出しを返します。

syms n x
laguerreL(n,x)

ans =
laguerreL(n, x)

一般化ラゲール多項式を求める

次数が n = 2 の一般化ラゲール多項式 L(n,a,x) の陽的な式を求めます。

syms a x
laguerreL(2,a,x)

ans =
(3*a)/2 - x*(a + 2) + a^2/2 + x^2/2 + 1

一般化ラゲール関数を返す

n が非負の整数でない場合、laguerreL(n,a,x) は一般化ラゲール関数を返します。

laguerreL(-2.7,3,2)

ans =
    0.2488

laguerreL は特定の入力について定義されず、エラーを返します。

syms x
laguerreL(-5/2, -3/2, x)

Error using symengine
Function 'laguerreL' not supported for parameter values '-5/2' and '-3/2'.

ベクトル入力および行列入力によりラゲール多項式を求める

n = [1 2] と指定して 1 次および 2 次のラゲール多項式を求めます。

syms x
laguerreL([1 2],x)

ans =
[ 1 - x, x^2/2 - 2*x + 1]

laguerreL は n の要素ごとに働き、2 つの要素をもつベクトルを返します。

複数の入力がベクトル、行列または多次元配列として指定されている場合、これらの入力は同じサイズでなければなりません。入力引数 n および x が行列の場合の一般化ラゲール多項式を求めます。

syms a
n = [2 3; 1 2];
xM = [x^2 11/7; -3.2 -x];
laguerreL(n,a,xM)

ans =
[ a^2/2 - a*x^2 + (3*a)/2 + x^4/2 - 2*x^2 + 1,...
      a^3/6 + (3*a^2)/14 - (253*a)/294 - 676/1029]
[                                    a + 21/5,...
          a^2/2 + a*x + (3*a)/2 + x^2/2 + 2*x + 1]

laguerreL は n および x の要素ごとに働き、n および x と同じサイズの行列を返します。

ラゲール多項式を微分して極限を求める

limit を使用して、x が無限大傾向をもつ場合の 3 次の一般化ラゲール多項式の範囲を求めます。

syms x
expr = laguerreL(3,2,x);
limit(expr,x,Inf)

ans =
-Inf

diff を使用して一般化ラゲール多項式 laguerreL(n,a,x) の 3 次導関数を求めます。

syms n a
expr = laguerreL(n,a,x);
diff(expr,x,3)

ans =
-laguerreL(n - 3, a + 3, x)

ラゲール多項式のテイラー級数展開を求める

taylor を使用して、x = 0 における 2 次の一般化ラゲール多項式のテイラー級数展開を求めます。

syms a x
expr = laguerreL(2,a,x);
taylor(expr,x)

ans =
(3*a)/2 - x*(a + 2) + a^2/2 + x^2/2 + 1

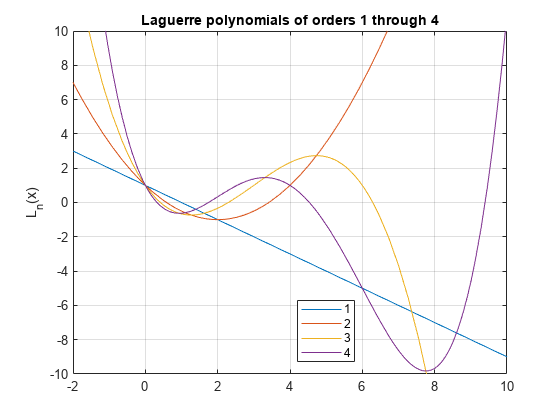
ラゲール多項式のプロット

1 次から 4 次のラゲール多項式をプロットします。

syms x
fplot(laguerreL(1:4,x))
axis([-2 10 -10 10])
grid on

ylabel('L_n(x)')
title('Laguerre polynomials of orders 1 through 4')
legend('1','2','3','4','Location','best')

入力引数

n — 多項式の次数

数値 | ベクトル | 行列 | 多次元配列 | シンボリック数 | シンボリック ベクトル | シンボリック行列 | シンボリック関数 | シンボリック多次元配列

多項式の次数。数値、ベクトル、行列、多次元配列、あるいはシンボリック数、ベクトル、行列、関数または多次元配列として指定します。

x — 入力

数値 | ベクトル | 行列 | 多次元配列 | シンボリック数 | シンボリック ベクトル | シンボリック行列 | シンボリック関数 | シンボリック多次元配列

入力。数値、ベクトル、行列、多次元配列、あるいはシンボリック数、ベクトル、行列、関数または多次元配列として指定します。

a — 入力

数値 | ベクトル | 行列 | 多次元配列 | シンボリック数 | シンボリック ベクトル | シンボリック行列 | シンボリック関数 | シンボリック多次元配列

入力。数値、ベクトル、行列、多次元配列、あるいはシンボリック数、ベクトル、行列、関数または多次元配列として指定します。

詳細

一般化ラゲール関数

一般化ラゲール関数は超幾何関数として次のように定義されます。

$$\text{laguerreL}\left(n,a,x\right)=\left(\begin{array}{c}n+a\\ a\end{array}\right){}_{1}F{}_1\left(-n;a+1;x\right).$$

n の非負の整数値に対し、この関数は次のスカラー積と直交する一般化ラゲール多項式を返します。

$$\langle f1,f2\rangle ={\displaystyle \underset{0}{\overset{\infty }{\int }}{e}^{-x}{x}^{a}f1\left(x\right)f2\left(x\right)dx}.$$

特に、一般化ラゲール多項式は次の正規化を満たします。

$$\langle \mathrm{laguerreL}\left(n,a,x\right),\mathrm{laguerreL}\left(m,a,x\right)\rangle =\{\begin{array}{cc}0& \text{if }n\ne m\\ \frac{\Gamma \left(a+n+1\right)}{n!}& \text{if }n=m.\end{array}$$

アルゴリズム

• パラメーター n および a のすべての値に対する一般化ラゲール関数は定義されていません。これは、超幾何関数定義内においてパラメーターに一定の制約が課されているためです。n と a の特定のペアに一般化ラゲール多項式が定義されていない場合、laguerreL 関数はエラー メッセージを返します。一般化ラゲール関数を返すを参照してください。

• 呼び出し laguerreL(n,x) と laguerreL(n,0,x) は同等です。

• n が非負の整数の場合、関数 laguerreL は対応するラゲール多項式の陽的な式を返します。

• 特殊な値 $$\mathrm{laguerreL}\left(n,a,0\right)=\left(\begin{array}{c}n+a\\ a\end{array}\right)$$ は任意の値 n および a において式を満たします。

• n が負の整数で、a が a ≥ -n を満たす非整数の数値である場合、laguerreL は 0 を返します。

• n が負の整数で、a が a < -n を満たす整数である場合、関数は次の反映ルールによって定義された陽的な式を返します。

  $$\mathrm{laguerreL}\left(n,a,x\right)={\left(-1\right)}^a{e}^x\mathrm{laguerreL}\left(-n-a-1,a,-x\right)$$

• すべての引数が数値で、少なくとも 1 つの引数が浮動小数点数である場合、laguerreL(x) は浮動小数点数を返します。その他すべての引数に対して laguerreL(n,a,x) はシンボリック関数呼び出しを返します。

バージョン履歴

R2014b で導入

参考

chebyshevT | chebyshevU | gegenbauerC | hermiteH | hypergeom | jacobiP | legendreP