gegenbauerC

ゲーゲンバウアー多項式

構文

gegenbauerC(n,a,x)

説明

gegenbauerC(n,a,x) は、点 x におけるパラメーター a をもつ n 次のゲーゲンバウアー (超球) 多項式を表します。

例

最初の 4 つのゲーゲンバウアー多項式

パラメーター a および変数 x に対する最初の 4 つのゲーゲンバウアー多項式を求めます。

syms a x
gegenbauerC([0, 1, 2, 3], a, x)

ans =
[ 1, 2*a*x, (2*a^2 + 2*a)*x^2 - a,...
((4*a^3)/3 + 4*a^2 + (8*a)/3)*x^3 + (- 2*a^2 - 2*a)*x]

数値引数およびシンボリック引数のゲーゲンバウアー多項式

引数に応じて、gegenbauerC は浮動小数点解またはシンボリック厳密解の結果を返します。

これらの点におけるパラメーター a = 1/3 に対する 5 次のゲーゲンバウアー多項式の値を求めます。これらの数値はシンボリック オブジェクトではないため、gegenbauerC は浮動小数点の結果を返します。

gegenbauerC(5, 1/3, [1/6, 1/4, 1/3, 1/2, 2/3, 3/4])

ans =
    0.1520    0.1911    0.1914    0.0672   -0.1483   -0.2188

シンボリック オブジェクトに変換された同じ数値に対する 5 次のゲーゲンバウアー多項式の値を求めます。シンボリック数に対し、gegenbauerC はシンボリック厳密解の結果を返します。

gegenbauerC(5, 1/3, sym([1/6, 1/4, 1/3, 1/2, 2/3, 3/4]))

ans =
[ 26929/177147, 4459/23328, 33908/177147, 49/729, -26264/177147, -7/32]

浮動小数点数によるチェビシェフ多項式の求解

gegenbauerC の直接呼び出しによるゲーゲンバウアー多項式の浮動小数点評価は数値的に安定しています。しかし、最初にシンボリック変数を使用して多項式を計算し、それからこの式に可変精度の値を代入すると数値的に不安定になる場合があります。

1/3 および vpa(1/3) におけるパラメーター 4 に対する 500 次のゲーゲンバウアー多項式の値を求めます。浮動小数点求解は数値的に安定しています。

gegenbauerC(500, 4, 1/3)
gegenbauerC(500, 4, vpa(1/3))

ans =
  -1.9161e+05
 
ans =
-191609.10250897532784888518393655

続いて、シンボリック多項式 C500 = gegenbauerC(500, 4, x) を求め、結果に x = vpa(1/3) を代入します。この方法は数値的に不安定です。

syms x
C500 = gegenbauerC(500, 4, x);
subs(C500, x, vpa(1/3))

ans =
-8.0178726380235741521208852037291e+35

vpa を使用して多項式の係数を近似し、結果に x = sym(1/3) を代入します。この方法も数値的に不安定です。

subs(vpa(C500), x, sym(1/3))

ans =
-8.1125412405858470246887213923167e+36

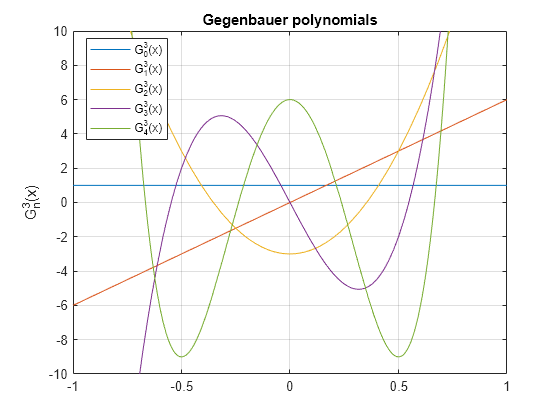
ゲーゲンバウアー多項式のプロット

パラメーター a = 3 に対する最初の 5 つのゲーゲンバウアー多項式をプロットします。

syms x y
fplot(gegenbauerC(0:4,3,x))
axis([-1 1 -10 10])
grid on

ylabel('G_n^3(x)')
title('Gegenbauer polynomials')
legend('G_0^3(x)', 'G_1^3(x)', 'G_2^3(x)', 'G_3^3(x)', 'G_4^3(x)',...
                                               'Location', 'Best')

入力引数

n — 多項式の次数

非負の整数 | シンボリック変数 | シンボリック式 | シンボリック関数 | ベクトル | 行列

多項式の次数。非負の整数、シンボリック変数、式または関数として、あるいは数値、シンボリック数、変数、式または関数のベクトルまたは行列として指定します。

a — パラメーター

数値 | シンボリック数 | シンボリック変数 | シンボリック式 | シンボリック関数 | ベクトル | 行列

パラメーター。非負の整数、シンボリック変数、式または関数、あるいは数値、シンボリック数、変数、式または関数のベクトルまたは行列として指定します。

x — 評価点

数値 | シンボリック数 | シンボリック変数 | シンボリック式 | シンボリック関数 | ベクトル | 行列

求解点。数値、シンボリック数、変数、式または関数、あるいは数値、シンボリック数、変数、式または関数のベクトルまたは行列として指定します。

詳細

ゲーゲンバウアー多項式

• ゲーゲンバウアー多項式は次の再帰式によって定義されます。

  $$G\left(0,a,x\right)=1,G\left(1,a,x\right)=2ax,G\left(n,a,x\right)=\frac{2x\left(n+a-1\right)}{n}G\left(n-1,a,x\right)-\frac{n+2a-2}{n}G\left(n-2,a,x\right)$$

• すべての実数 a > -1/2 に対して、ゲーゲンバウアー多項式は区間 -1 ≤ x ≤ 1 において重み関数 $$w\left(x\right)={\left(1-x^2\right)}^{a-\frac{1}{2}}$$ と直交します。

  $${\displaystyle \underset{-1}{\overset{1}{\int }}G(n,a,x)G(m,a,x){\left(1-x^2\right)}^{a-1/2}dx}=\{\begin{array}{cc}0& \text{if }n\ne m\\ \frac{\pi 2^{1-2a}\Gamma \left(n+2a\right)}{n!\left(n+a\right){\left(\Gamma \left(a\right)\right)}^2}& \text{if }n=m.\end{array}$$

• 第 1 種および第 2 種チェビシェフ多項式は、ゲーゲンバウアー多項式の特殊なケースです。

  $$T\left(n,x\right)=\{\begin{array}{cc}\frac{1}{2}\underset{a\to 0}{\lim }\frac{n+a}{a}G\left(n,a,x\right)& \text{if }n\ne 0\\ \underset{a\to 0}{\lim }G\left(0,a,x\right)=1& \text{if }n=0\end{array}$$

  $$U\left(n,x\right)=G\left(n,1,x\right)$$

• ルジャンドル多項式もゲーゲンバウアー多項式の特別なケースです。

  $$P\left(n,x\right)=G\left(n,\frac{1}{2},x\right)$$

ヒント

• gegenbauerC は、シンボリック オブジェクトではない数値引数に対し浮動小数点の結果を返します。

• gegenbauerC は非スカラー入力の要素ごとに働きます。

• 非スカラー引数はすべて同じサイズでなければなりません。1 つまたは 2 つの入力引数が非スカラーの場合、gegenbauerC はスカラーを、非スカラー引数と同じサイズの、すべての要素が対応するスカラーと等しいベクトルまたは行列に拡張します。

参照

[1] Hochstrasser, U. W. “Orthogonal Polynomials.” Handbook of Mathematical Functions with Formulas, Graphs, and Mathematical Tables. (M. Abramowitz and I. A. Stegun, eds.). New York: Dover, 1972.

[2] Cohl, Howard S., and Connor MacKenzie. “Generalizations and Specializations of Generating Functions for Jacobi, Gegenbauer, Chebyshev and Legendre Polynomials with Definite Integrals.” Journal of Classical Analysis, no. 1 (2013): 17–33. https://doi.org/10.7153/jca-03-02.

バージョン履歴

R2014b で導入

参考

chebyshevT | chebyshevU | hermiteH | jacobiP | laguerreL | legendreP