Main Content

このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

jacobiDN

ヤコビ DN 楕円関数

ページ内をすべて折りたたむ

構文

jacobiDN(u,m)

説明

jacobiDN(u,m) は、u および m で与えられるヤコビ DN 楕円関数を返します。u または m が配列の場合、jacobiDN は要素単位で動作します。

例

例

すべて折りたたむ

jacobiDN(2,1)
ans =
    0.2658

配列を入力として jacobiDN を呼び出します。u または m が配列の場合、jacobiDN は要素単位で動作します。

jacobiDN([2 1 -3],[1 2 3])
ans =
    0.2658    0.3107   -0.0046

sym を使用して数値入力をシンボリック型に変換し、ヤコビ DN 楕円関数を求めます。u = 0 または m = 0 または 1 の場合、jacobiDN はシンボリックな入力に対してシンボリック厳密解の出力を返します。

jacobiDN(sym(2),sym(1))
ans =
1/cosh(2)

u および m がそれ以外のシンボリック値である場合、jacobiDN は未評価の関数呼び出しを返すことを示します。

jacobiDN(sym(2),sym(3))
ans =
jacobiDN(2, 3)

シンボリックな変数または式に対して、jacobiDN は未評価の関数呼び出しを返します。

syms x y
f = jacobiDN(x,y)
f =
jacobiDN(x, y)

subs を使用して変数に値を代入し、double を使用して値を double に変換します。

f = subs(f, [x y], [3 5])
f =
jacobiDN(3, 5)
fVal = double(f)
fVal =
    0.9976

vpa を使用して f をより高精度に計算します。

fVal = vpa(f)
fVal =
0.99757205953668099307853539907267
ライブ スクリプトを開く

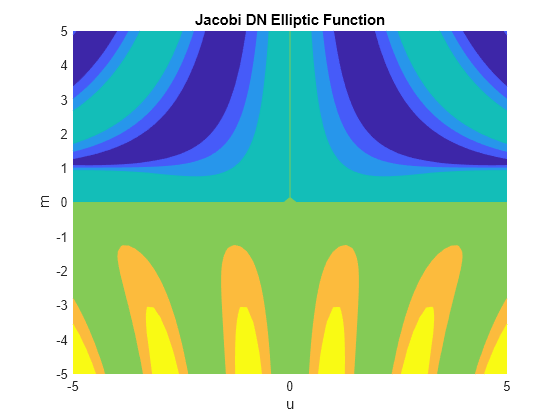
fcontour を使用してヤコビ DN 楕円関数をプロットします。変数の並びが (u,m) のシンボリック関数 f を使用して、u を X 軸上に、m を Y 軸上に設定します。Fill を on に設定して、等高線図を塗りつぶします。

syms f(u,m)
f(u,m) = jacobiDN(u,m);
fcontour(f,'Fill','on')
title('Jacobi DN Elliptic Function')
xlabel('u')
ylabel('m')

入力引数

すべて折りたたむ

入力。数値、ベクトル、行列または多次元配列、あるいはシンボリック数、変数、ベクトル、行列、多次元配列、関数または式として指定します。

入力。数値、ベクトル、行列または多次元配列、あるいはシンボリック数、変数、ベクトル、行列、多次元配列、関数または式として指定します。

詳細

すべて折りたたむ

ヤコビ DN 楕円関数

ヤコビ DN 楕円関数は次のとおりです。

dn(u,m)=1−msin(ϕ)2

ここで、ϕ は、F(ϕ,m) = u および F が第 1 種不完全楕円積分を表すような値です。F は ellipticF として実装されます。

ヤコビ楕円関数は、周期 4K(m) および 4iK'(m) の第 1 引数において有理型で二重周期です。ここで、K は第 1 種完全楕円積分であり、ellipticK として実装されます。

バージョン履歴

R2017b で導入

参考

| | | | | | | | | | | | |