ランダム フォレストの予測子の選択

この例では、回帰木のランダム フォレストを成長させるときに、データ セットに適した分割予測子選択手法を選択する方法を示します。また、学習データに含める最も重要な予測子を決定する方法も示します。

データの読み込みと前処理

carbig データ セットを読み込みます。与えられた気筒数、エンジン排気量、馬力、重量、加速、モデル年および生産国に対して自動車の燃費を予測するモデルを考えます。Cylinders、Model_Year および Origin はカテゴリカル変数であるとします。

load carbig
Cylinders = categorical(Cylinders);
Model_Year = categorical(Model_Year);
Origin = categorical(cellstr(Origin));
X = table(Cylinders,Displacement,Horsepower,Weight,Acceleration,Model_Year,Origin);

予測子内のレベルの測定

標準 CART アルゴリズムには、一意な値 (レベル) が少ない予測子 (カテゴリカル変数など) よりも、多数のレベルをもつ予測子 (連続変数など) を分割する傾向があります。データが異種混合である場合、または予測子変数間でレベルの数が大きく異なる場合は、標準 CART ではなく曲率検定または交互作用検定を分割予測子選択に使用することを検討してください。

各予測子について、データ内のレベルの数を測定します。これを行う方法の 1 つとして、次のような無名関数を定義します。

1. categorical を使用してすべての変数をカテゴリカル データ型に変換する

2. categories を使用してすべての一意なカテゴリを決定し、欠損値は無視する

3. numel を使用してカテゴリの個数を数える

次に、varfun を使用してこの関数を各変数に適用します。

countLevels = @(x)numel(categories(categorical(x)));
numLevels = varfun(countLevels,X,'OutputFormat','uniform');

予測子変数間でレベルの数を比較します。

figure
bar(numLevels)
title('Number of Levels Among Predictors')
xlabel('Predictor variable')
ylabel('Number of levels')
h = gca;
h.XTickLabel = X.Properties.VariableNames(1:end-1);
h.XTickLabelRotation = 45;
h.TickLabelInterpreter = 'none';

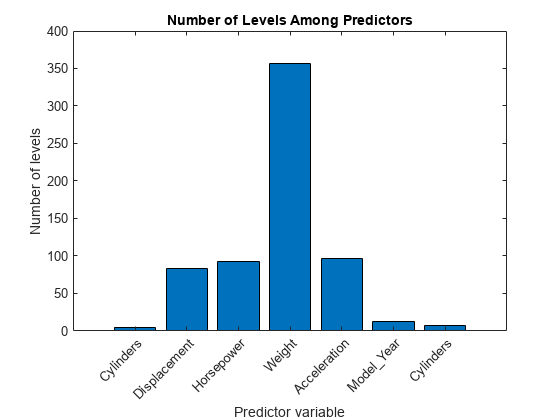
連続変数には、カテゴリカル変数より多くのレベルがあります。レベル数は予測子によって大きく異なるので、標準 CART を使用してランダム フォレストの木の各ノードで分割予測子を選択すると、予測子の重要度の推定が不正確になる可能性があります。このようなケースでは、曲率検定または交互作用検定を使用します。アルゴリズムを指定するには、名前と値のペアの引数 'PredictorSelection' を使用します。詳細は、分割予測子選択手法の選択を参照してください。

回帰木のバギング アンサンブルに学習をさせる

バギングされた 200 本の回帰木のアンサンブルに学習をさせて、予測子の重要度の値を推定します。以下の名前と値のペアの引数を使用して、木学習器を定義します。

• 'NumVariablesToSample','all' — すべての予測子変数が各木で使用されることを保証するため、すべての予測子変数を各ノードで使用します。

• 'PredictorSelection','interaction-curvature' — 交互作用検定を使用して分割予測子を選択するよう指定します。

• 'Surrogate','on' — データ セットに欠損値が含まれているので、精度を高めるために代理分岐を使用するよう指定します。

t = templateTree('NumVariablesToSample','all',...
    'PredictorSelection','interaction-curvature','Surrogate','on');
rng(1); % For reproducibility
Mdl = fitrensemble(X,MPG,'Method','Bag','NumLearningCycles',200, ...
    'Learners',t);

Mdl は RegressionBaggedEnsemble モデルです。

out-of-bag 予測を使用して $$R^2$$ のモデルを推定します。

yHat = oobPredict(Mdl);
R2 = corr(Mdl.Y,yHat)^2

R2 = 0.8744

Mdl は、平均の周辺で変動性の 87% を説明します。

予測子の重要度の推定

木同士で out-of-bag 観測値の順序を変更することにより、予測子の重要度の値を推定します。

impOOB = oobPermutedPredictorImportance(Mdl);

impOOB は予測子の重要度の推定が格納されている 1 行 7 列のベクトルで、Mdl.PredictorNames 内の予測子に対応しています。この推定は、多くのレベルが含まれている予測子に偏ってはいません。

予測子の重要度の推定を比較します。

figure
bar(impOOB)
title('Unbiased Predictor Importance Estimates')
xlabel('Predictor variable')
ylabel('Importance')
h = gca;
h.XTickLabel = Mdl.PredictorNames;
h.XTickLabelRotation = 45;
h.TickLabelInterpreter = 'none';

重要度の推定値が大きいほど重要な予測子です。棒グラフは、最も重要な予測子が Model_Year であり、次に重要なのは Cylinders と Weight であることを示しています。変数 Model_Year および Cylinders の異なるレベルはそれぞれ 13 個および 5 個ですが、変数 Weight には 300 個以上のレベルがあります。

out-of-bag 観測値およびそれらの推定の順序を変更して予測子の重要度の推定を比較します。推定は、各予測子の分割による平均二乗誤差のゲインを合計して得られます。また、代理分岐によって推定した予測子の関連尺度を取得します。

[impGain,predAssociation] = predictorImportance(Mdl);

figure
plot(1:numel(Mdl.PredictorNames),[impOOB' impGain'])
title('Predictor Importance Estimation Comparison')
xlabel('Predictor variable')
ylabel('Importance')
h = gca;
h.XTickLabel = Mdl.PredictorNames;
h.XTickLabelRotation = 45;
h.TickLabelInterpreter = 'none';
legend('OOB permuted','MSE improvement')
grid on

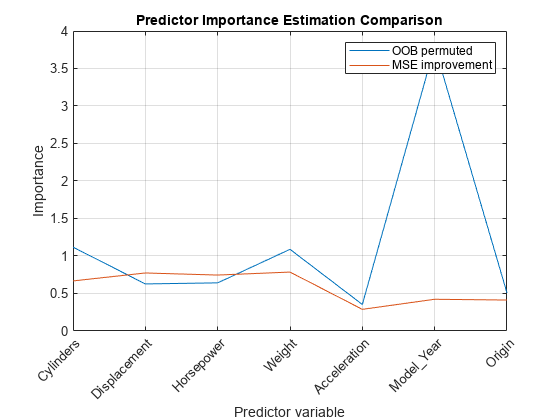
impGain の値によると、変数 Displacement、Horsepower および Weight は同じように重要であるようです。

predAssociation は予測子の関連尺度が格納されている 7 行 7 列の行列です。行と列は Mdl.PredictorNames の予測子に対応します。関連性予測尺度は、観測値を分割する決定規則間の類似度を示す値です。最適な代理決定分岐は関連性予測尺度が最大になります。predAssociation の要素を使用すると、予測子のペア間における関連性の強さを推定できます。値が大きいほど予測子のペアの関連性が高くなります。

figure
imagesc(predAssociation)
title('Predictor Association Estimates')
colorbar
h = gca;
h.XTickLabel = Mdl.PredictorNames;
h.XTickLabelRotation = 45;
h.TickLabelInterpreter = 'none';
h.YTickLabel = Mdl.PredictorNames;

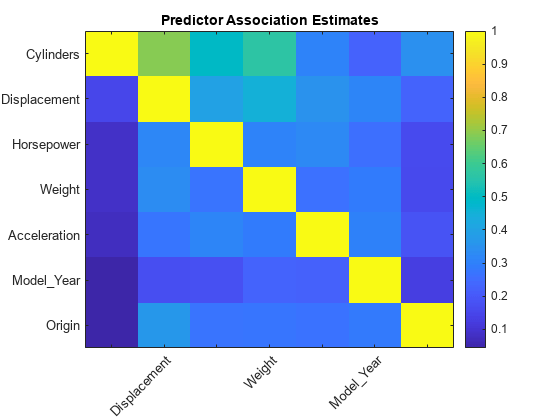
predAssociation(1,2)

ans = 0.6871

最大の関連は Cylinders と Displacement の間にありますが、2 つの予測子の間に強い関係があることを示すほど大きい値ではありません。

縮小した予測子セットの使用によるランダム フォレストの成長

ランダム フォレスト内の予測子数が増えると予測時間が長くなるので、可能な限り少ない個数の予測子を使用してモデルを作成することが推奨されます。

最良の 2 つの予測子のみを使用して、200 本の回帰木が含まれているランダム フォレストを成長させます。templateTree の 'NumVariablesToSample' の既定値は、回帰の場合は予測子の個数の 1/3 なので、fitrensemble はランダム フォレスト アルゴリズムを使用します。

t = templateTree('PredictorSelection','interaction-curvature','Surrogate','on', ...
    'Reproducible',true); % For reproducibility of random predictor selections
MdlReduced = fitrensemble(X(:,{'Model_Year' 'Weight'}),MPG,'Method','Bag', ...
    'NumLearningCycles',200,'Learners',t);

縮小したモデルの $$R^2$$ を計算します。

yHatReduced = oobPredict(MdlReduced);
r2Reduced = corr(Mdl.Y,yHatReduced)^2

r2Reduced = 0.8653

縮小したモデルの $$R^2$$ は完全なモデルの $$R^2$$ に近くなっています。この結果は、縮小したモデルが予測に十分であることを示しています。

参考

templateTree | fitrensemble | oobPredict | oobPermutedPredictorImportance | predictorImportance | corr

関連するトピック

• 分類木および回帰木の改善
• TreeBagger の使用による回帰木の bootstrap aggregation (バギング)
• 代理分岐
• 特徴選択の紹介
• 機械学習モデルの解釈