TreeBagger の使用による回帰木の bootstrap aggregation (バギング)

Statistics and Machine Learning Toolbox™ には、回帰木の bootstrap aggregation (バギング) をサポートするオブジェクトとして、TreeBagger を使用して作成されるTreeBaggerおよびfitrensembleを使用して作成されるRegressionBaggedEnsembleという 2 つのオブジェクトがあります。TreeBagger と RegressionBaggedEnsemble の違いについては、TreeBagger とバギング アンサンブルの比較を参照してください。

この例では、TreeBagger のみの機能を使用する回帰のワークフローを示します。

205 個の観測値、25 個の予測子、および 1 つの応答 (保険リスク ランク付けを表す "symboling") が含まれている、1985 年の自動車輸入のデータベースを使用します。最初の 15 個の変数は数値で、最後の 10 個は categorical です。シンボル インデックスは、-3 ～ 3 の整数です。

データ セットを読み込み、それを予測子と応答の配列に分割します。

load imports-85
Y = X(:,1);
X = X(:,2:end);
isCategorical = [zeros(15,1);
                 ones(size(X,2)-15,1)]; % Categorical variable flag

バギングがランダム化されたデータ図を使用するため、その正確な結果は最初の乱数シードにより異なります。この例で結果を再生するには、ランダム ストリーム設定を使用します。

rng(1945,'twister')

最適なリーフ サイズの探索

回帰の場合、原則として葉のサイズを 5 に設定し、決定分岐のための入力特徴量の 3 分の 1 を無作為に選択します。以下の手順で、さまざまな葉のサイズを使用して、回帰によって取得された平均二乗誤差を比較することにより、最適な葉のサイズを確認してください。oobError は、MSE と成長したツリーの数を計算します。後で out-of-bag 予測を取得するために、OOBPred を 'On' に設定しなければなりません。

leaf = [5 10 20 50 100];
col = 'rbcmy';
figure
hold on
for i=1:length(leaf)
    b = TreeBagger(50,X,Y,'Method','regression', ...
        'OOBPrediction','On', ...
        'CategoricalPredictors',find(isCategorical == 1), ...
        'MinLeafSize',leaf(i));
    plot(oobError(b),col(i))
end
xlabel('Number of Grown Trees')
ylabel('Mean Squared Error') 
legend({'5' '10' '20' '50' '100'},'Location','NorthEast')
hold off

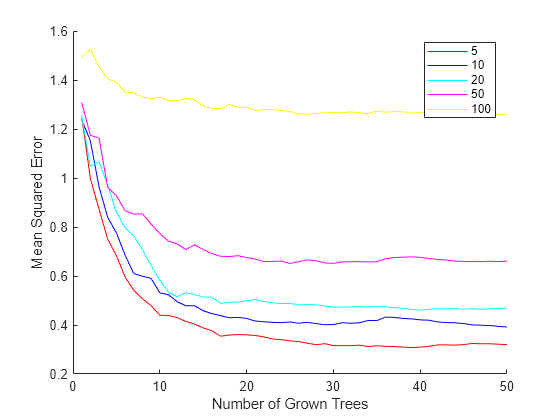
赤い曲線 (葉のサイズ 5) は最も低い MSE 値です。

特徴量重要度の推定

実際に応用する場合、数百本のツリーでアンサンブルを成長させるのが普通です。たとえば、前述のコード ブロックでは 50 個のツリーを使用して処理を高速化しています。これで最適な葉のサイズを推定したので、100 本のツリーでより大きなアンサンブルを成長させ、それを使用して特徴量の重要度を推定してみましょう。

b = TreeBagger(100,X,Y,'Method','regression', ...
    'OOBPredictorImportance','On', ...
    'CategoricalPredictors',find(isCategorical == 1), ...
    'MinLeafSize',5);

誤差曲線を再び調べ、学習中に誤りがなかったことを確認します。

figure
plot(oobError(b))
xlabel('Number of Grown Trees')
ylabel('Out-of-Bag Mean Squared Error')

予測機能は、些末な特徴量ではなく、より重要な特徴量に依存しなければなりません。このアイデアを使用して、特徴量の重要度を計測することができます。

特徴に関しては、データ セット内の観測全体で、特徴ごとに値を並べ替えます。次に MSE がどのくらい低下するかを測定できます。特徴ごとにこれを繰り返すことができます。

各入力変数間の out-of-bag 観測値の並べ替えに起因する MSE の増加をプロットします。OOBPermutedPredictorDeltaError 配列は、変数ごとにアンサンブル内のすべてのツリーで平均化し、ツリーから取得した標準偏差で割った MSE の増加を格納します。この値が大きいほど、変数はより重要になります。0.7 で任意に切り捨てることにより、4 つの最も重要な特徴量を選択できます。

figure
bar(b.OOBPermutedPredictorDeltaError)
xlabel('Feature Number') 
ylabel('Out-of-Bag Feature Importance')

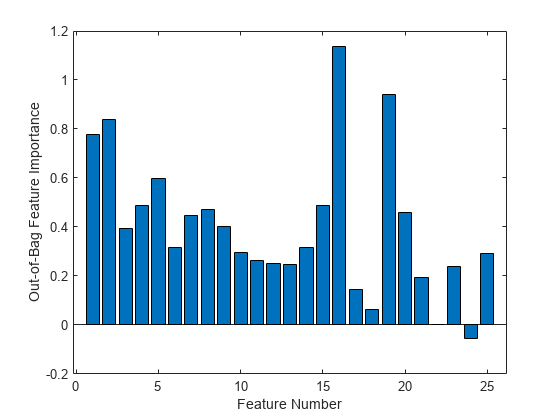
idxvar = find(b.OOBPermutedPredictorDeltaError>0.7)

idxvar = 1×4

     1     2    16    19

idxCategorical = find(isCategorical(idxvar)==1);

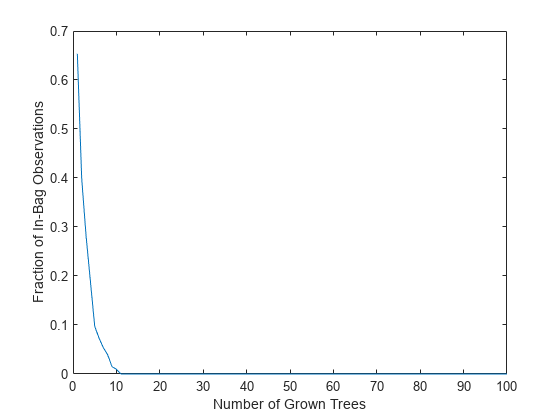
TreeBagger の OOBIndices プロパティは、どの観測がどのツリーの out-of-bag であるかを追跡します。このプロパティを使用して、すべてのツリーにまとめられた学習データの観測比率を監視することができます。曲線は約 2/3 の地点 (1 つのブートストラップ複製により選択された固有の観測の比率) で開始し、約 10 本のツリーの地点で 0 に下がります。

finbag = zeros(1,b.NTrees);
for t=1:b.NTrees
    finbag(t) = sum(all(~b.OOBIndices(:,1:t),2));
end
finbag = finbag/size(X,1);
figure
plot(finbag)
xlabel('Number of Grown Trees')
ylabel('Fraction of In-Bag Observations')

特徴量の数を絞ってツリーを成長させる

最も強力な 4 つの特徴量を使用して、同じような予測力を得ることができるかどうかを判定します。まず、これらの特徴量のみで 100 本のツリーを成長させます。選択した 4 つの特徴量は、最初の 2 つが数値、残りの 2 つがカテゴリカルです。

b5v = TreeBagger(100,X(:,idxvar),Y, ...
    'Method','regression','OOBPredictorImportance','On', ...
    'CategoricalPredictors',idxCategorical,'MinLeafSize',5);
figure
plot(oobError(b5v))
xlabel('Number of Grown Trees')
ylabel('Out-of-Bag Mean Squared Error')

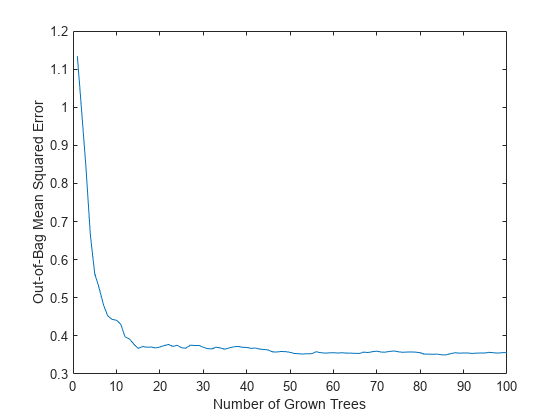
figure
bar(b5v.OOBPermutedPredictorDeltaError)
xlabel('Feature Index')
ylabel('Out-of-Bag Feature Importance')

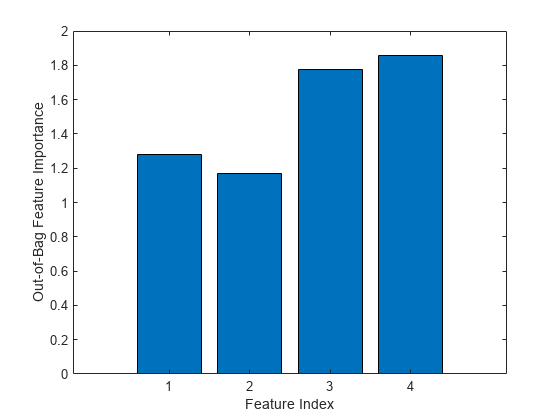
この最強の 4 つの特徴量にはフル セットと同じ MSE があり、縮小したセットで学習を行ったアンサンブルはこれらの特徴量を互いに対して同じようにランク付けします。数を絞り込んだセットから特徴 1 および 2 を削除すると、アルゴリズムの予測力が大幅に減少しない可能性もあります。

外れ値の探索

学習データ内の外れ値を見つけるには、fillProximities を使用して、近接行列を計算します。

b5v = fillProximities(b5v);

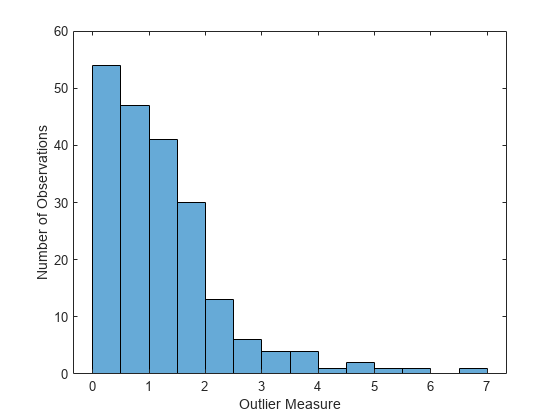
このメソッドでは、標本全体に対する平均外れ値予測を減算することにより、この測定値が正規化されます。その後、この差異の大きさが取得され、その結果が標本全体に対する中央絶対偏差で除算されます。

figure
histogram(b5v.OutlierMeasure)
xlabel('Outlier Measure')
ylabel('Number of Observations')

データ内のクラスターを発見する

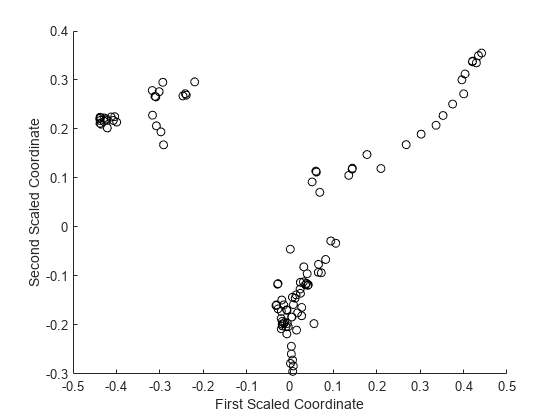
多次元尺度構成法を近接行列に適用すると、入力データの構造を検査し、観測の可能なクラスターを探すことができます。mdsProx メソッドは、計算近接行列のためにスケーリングされた座標と固有値を返します。Colors 名前と値のペアの引数でこのメソッドを実行すると、スケーリングされた 2 つの座標の散布図が作成されます。

figure
[~,e] = mdsProx(b5v,'Colors','K');
xlabel('First Scaled Coordinate')
ylabel('Second Scaled Coordinate')

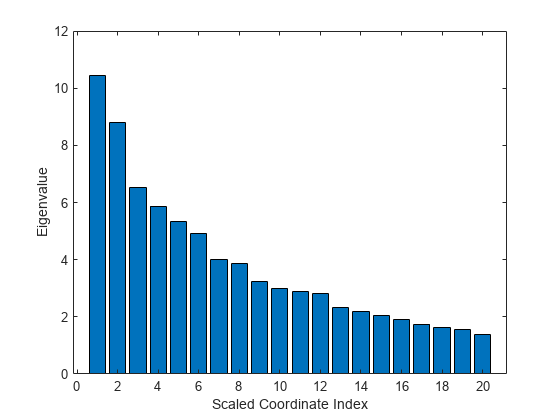
最初の 20 個の固有値をプロットすることにより、スケーリングした軸の相対的な重要性を評価します。

figure
bar(e(1:20))
xlabel('Scaled Coordinate Index')
ylabel('Eigenvalue')

将来使用するためにアンサンブル構成を保存する

学習したアンサンブルを使用して未観測データの応答を予測する場合は、ディスクにアンサンブルを格納し、後でそれを取り出します。out-of-bag データの予測の計算や、他の方法による学習データの再利用を行わない場合は、アンサンブル オブジェクト自体を格納する必要がありません。その場合は、アンサンブルのコンパクトなバージョンを保存するだけで十分です。以下のように、アンサンブルからコンパクトなオブジェクトを抽出します。

c = compact(b5v)

c = 
  CompactTreeBagger
Ensemble with 100 bagged decision trees:
              Method:           regression
       NumPredictors:                    4

生成される CompactTreeBagger モデルは *.mat ファイルに保存できます。

参考

TreeBagger | compact | oobError | mdsprox | fillprox | fitrensemble

関連するトピック

• TreeBagger の使用による分類木の bootstrap aggregation (バギング)
• TreeBagger とバギング アンサンブルの比較
• 回帰 TreeBagger ワークフローに対する並列処理の使用