このページの翻訳は最新ではありません。ここをクリックして、英語の最新版を参照してください。

TreeBagger の使用による分類木の bootstrap aggregation (バギング)

Statistics and Machine Learning Toolbox™ には、分類木の bootstrap aggregation (バギング) をサポートするオブジェクトとして、TreeBagger を使用して作成されるTreeBaggerおよびfitcensembleを使用して作成されるClassificationBaggedEnsembleという 2 つのオブジェクトがあります。TreeBagger と ClassificationBaggedEnsemble の違いについては、TreeBagger とバギング アンサンブルの比較を参照してください。

この例では、TreeBagger のみの機能を使用する分類のワークフローを示します。

351 個の観測値と 34 個の実数予測子が含まれている、電離層のデータを使用します。応答変数は、以下の 2 つのレベルをもつカテゴリです。

• 'g' はレーダー反射が良好であることを表します。

• 'b' はレーダー反射が不良であることを表します。

目標は、34 回の測定のセットを使用して、反射の良し悪しを予測することです。

初期乱数シードを固定し、50 本のツリーを成長させ、アンサンブル誤差がツリーの累積と交替する様子を調べ、特徴量の重要度を推定します。分類するための最良の方法は、最小のリーフ サイズを 1 に設定し、無作為に分割した決定ごとに特徴量の総数の平方根を選択することです。これらの設定は、分類に使用する TreeBagger の既定の設定です。

load ionosphere
rng(1945,'twister')
b = TreeBagger(50,X,Y,'OOBPredictorImportance','On');
figure
plot(oobError(b))
xlabel('Number of Grown Trees')
ylabel('Out-of-Bag Classification Error')

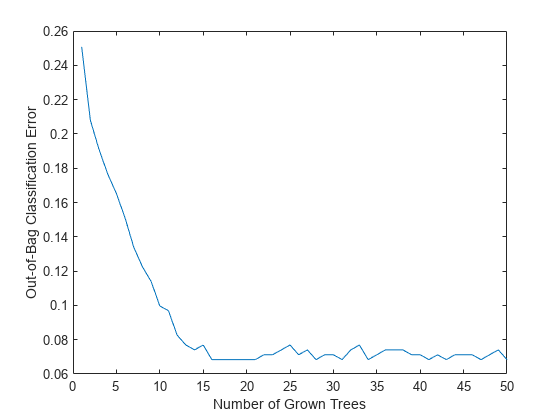
この方法では、観測するツリーがほとんどないアンサンブルが学習されます。すべてのツリーに対して観測は in-bag です。このような観測では、真の out-of-bag 予測を計算することは不可能であり、TreeBagger は分類用に最も確からしいクラスを返し、回帰用に標本平均を返します。DefaultYfit プロパティを使用して、in-bag 観測用に返される既定値を変更することができます。分類用の既定値を空の文字ベクトルに設定すると、out-of-bag 誤差の計算から in-bag の観測値が除外されます。この例では、ツリーの数が少ないと、曲線はより可変になります。理由は、観測によっては out-of-bag にならないこと (そのため除外されること)、または、ツリーの存在なしに予測するからです。

b.DefaultYfit = '';
figure
plot(oobError(b))
xlabel('Number of Grown Trees')
ylabel('Out-of-Bag Error Excluding In-Bag Observations')

TreeBagger の OOBIndices プロパティは、どの観測がどのツリーの out-of-bag であるかを追跡します。このプロパティを使用して、すべてのツリーにまとめられた学習データの観測比率を監視することができます。曲線は約 2/3 の地点 (1 つのブートストラップ複製により選択された固有の観測の比率) で開始し、約 10 本のツリーの地点で 0 に下がります。

finbag = zeros(1,b.NumTrees);
for t=1:b.NTrees
    finbag(t) = sum(all(~b.OOBIndices(:,1:t),2));
end
finbag = finbag / size(X,1);
figure
plot(finbag)
xlabel('Number of Grown Trees')
ylabel('Fraction of In-Bag Observations')

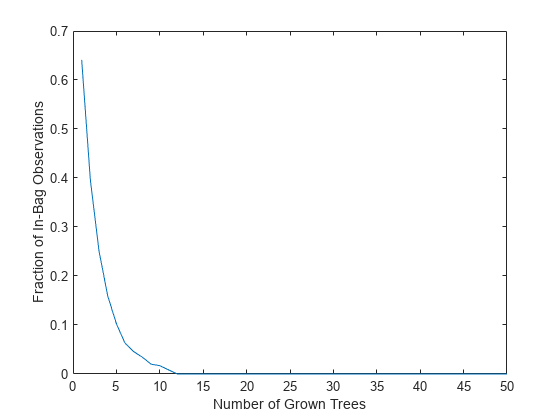
特徴量の重要度を推定します。

figure
bar(b.OOBPermutedPredictorDeltaError)
xlabel('Feature Index')
ylabel('Out-of-Bag Feature Importance')

重要度が 0.75 より大きくなる特徴量を選択します。このしきい値は任意に選択したものです。

idxvar = find(b.OOBPermutedPredictorDeltaError>0.75)

idxvar = 1×5

     3     5     7     8    27

最も重要な特徴量を選択したので、縮小した特徴セットで、より大きなアンサンブルを成長させます。制限した特徴セットでは、out-of-bag 観測を変換せずに特徴量の重要度の新しい推定を取得することにより、時間を節約します (OOBVarImp を 'off' に設定)。分類誤差の out-of-bag 推定を取得することにしましょう (OOBPred を 'on' に設定)。

b5v = TreeBagger(100,X(:,idxvar),Y,'OOBPredictorImportance','off','OOBPrediction','on');
figure
plot(oobError(b5v))
xlabel('Number of Grown Trees')
ylabel('Out-of-Bag Classification Error')

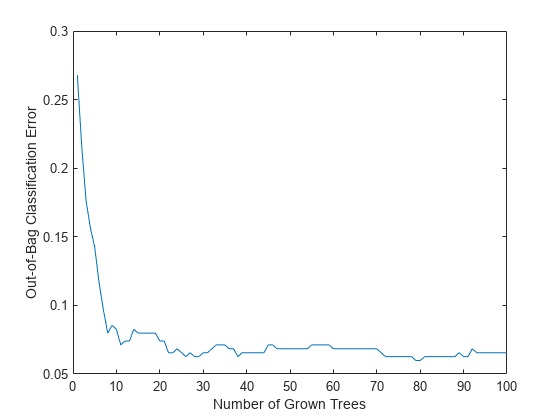
アンサンブル分類の場合は、分類誤差 (誤って分類された観測の比率) に加えて、平均分類マージンを監視することもできます。観測ごとに、margin は、真のクラスのスコアおよびこのツリーが予測する他のクラスの最大スコアの差として定義されます。累積分類マージンはすべてのツリー全体の平均スコアを使用します。平均累積分類マージンはすべての観測全体の平均累積マージンです。'cumulative' (既定の設定) に設定された 'mode' 引数をもつ oobMeanMargin メソッドは、アンサンブルが成長するにつれて平均累積マージンが変わる様子を示します。返された配列内のすべての新要素は、新しいツリーをアンサンブルに含めることにより得た累積マージンを表します。学習が成功すると、平均分類マージンのゆるやかな増加が見えるはずです。

この方法では、観測するツリーがほとんどないアンサンブルが学習されます。すべてのツリーに対して観測は in-bag です。このような観測では、真の out-of-bag 予測を計算することは不可能であり、TreeBagger は分類用に最も確からしいクラスを返し、回帰用に標本平均を返します。

決定木の場合、分類スコアは、ツリーのリーフにおけるクラスのインスタンスを観測する際の確率です。たとえば、成長した決定木のリーフがその観測を学習している 5 つの 'good' と 3 つの 'bad' をもつ場合は、このリーフになるすべての観測に対してこの決定木が返すスコアは、'good' クラスの 5/8 と 'bad' クラスの 3/8 です。これらの確率は 'scores' と呼ばれ、返された予測の数値に明白に解釈できない、他の分類器との整合性を表します。

figure
plot(oobMeanMargin(b5v));
xlabel('Number of Grown Trees')
ylabel('Out-of-Bag Mean Classification Margin')

近接行列を計算し、外れ値の尺度の分布を調べます。回帰と異なり、アンサンブル分類用の外れ値の測定は、各クラス内で別々に計算されます。

b5v = fillProximities(b5v);
figure
histogram(b5v.OutlierMeasure)
xlabel('Outlier Measure')
ylabel('Number of Observations')

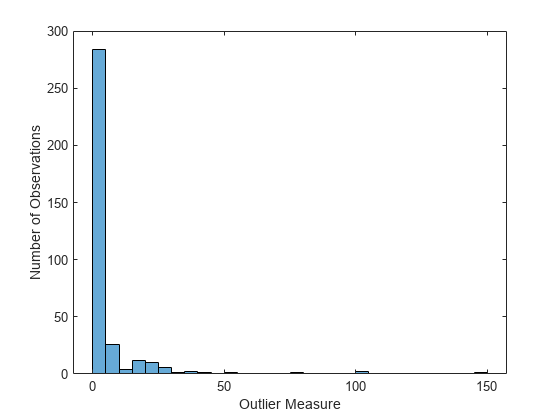
極端な外れ値のクラスを見つけます。

extremeOutliers = b5v.Y(b5v.OutlierMeasure>40)

extremeOutliers = 6x1 cell
    {'g'}
    {'g'}
    {'g'}
    {'g'}
    {'g'}
    {'g'}

percentGood = 100*sum(strcmp(extremeOutliers,'g'))/numel(extremeOutliers)

percentGood = 100

すべての極端な外れ値に 'good' というラベルが付けられています。

回帰については、mdsProx の 'Colors' 名前と値のペア引数を使用して、異なる色で 2 クラスを表示し、スケーリングした座標をプロットすることができます。この引数は文字ベクトルを取り、すべての文字は色を表します。クラス名のランク付けはされません。そのため、アンサンブル内の ClassNames プロパティにおけるクラスの位置を特定することが推奨されます。

gPosition = find(strcmp('g',b5v.ClassNames))

gPosition = 2

'bad' クラスが 1 つ目で 'good' クラスが 2 つ目です。'bad' クラスでは赤、'good' クラスでは青を観測値に使用して、スケーリングされた座標を表示します。

figure
[s,e] = mdsProx(b5v,'Colors','rb');
xlabel('First Scaled Coordinate')
ylabel('Second Scaled Coordinate')

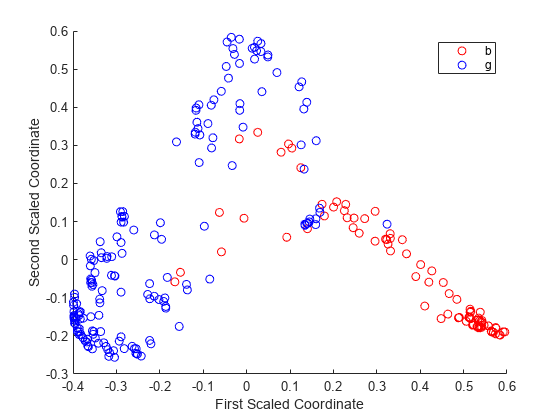
スケーリングにより取得した最初の 20 個の固有値をプロットします。最初の固有値が明らかに優勢であり、最初にスケーリングされた座標が最も重要です。

figure
bar(e(1:20))
xlabel('Scaled Coordinate Index')
ylabel('Eigenvalue')

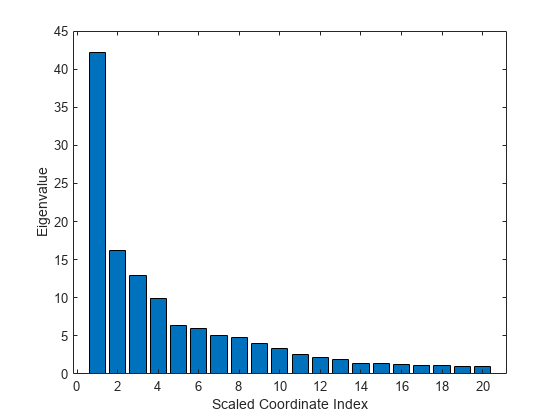
アンサンブル分類の性能を探究するもう 1 つの方法は、受信者動作特性 (ROC) 曲線または現在の課題に適する別の性能曲線をプロットすることです。out-of-bag 観測に対する予測を取得します。アンサンブル分類の場合、oobPredict メソッドは、最初の出力引数として分類ラベルの cell 配列を返し、2 つ目の出力引数としてスコアの数値配列を返します。返されたステレオの配列はクラスごとに 1 列、合計 2 列になります。この場合、1 列目が 'bad' クラスで 2 列目が 'good' クラスです。スコア行列内の列の 1 つは冗長です。その理由は、スコアがツリーのリーフ内のクラス確率と合計 1 になる定義によるクラス確率を表すからです。

[Yfit,Sfit] = oobPredict(b5v);

rocmetrics を使用して性能曲線を計算します。rocmetricsは、既定では ROC 曲線の真陽性率と偽陽性率を計算します。

rocObj = rocmetrics(b5v.Y,Sfit(:,gPosition),'g');

rocmetrics の関数 plot を使用して、'good' のクラスの ROC 曲線をプロットします。

plot(rocObj)

標準の ROC 曲線の代わりに、たとえば、'good' クラスのためのスコアにアンサンブル精度対しきい値の座標をプロットするとよいでしょう。rocmetrics の関数 addMetrics を使用して精度を計算します。精度は正しく分類された観測の比率か、1 マイナス分類誤差と同じです。

rocObj = addMetrics(rocObj,'Accuracy');

アンサンブルの精度としきい値の関係を示すプロットを作成します。

thre = rocObj.Metrics.Threshold;
accu = rocObj.Metrics.Accuracy;
plot(thre,accu)
xlabel('Threshold for ''good'' Returns')
ylabel('Classification Accuracy')

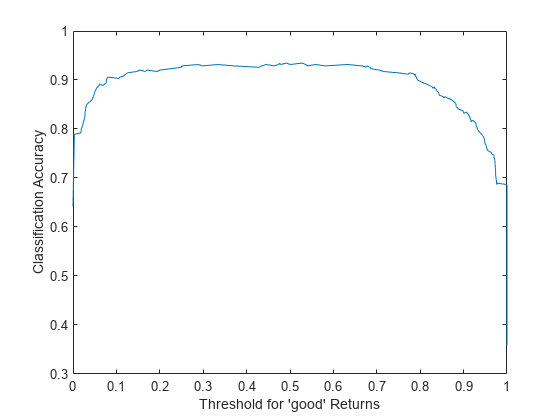
曲線は、0.2 ～ 0.6 のしきい値が妥当な選択であることを示す平らな領域を示します。既定の設定では、分類モデルは、2 クラスの間で境界として 0.5 を使用し、分類ラベルを割り当てます。これがどの精度に対応するのかを正確に見つけることができます。

[~,idx] = min(abs(thre-0.5));
accu(idx)

ans = 0.9316

最大精度を求めます。

[maxaccu,iaccu] = max(accu)

maxaccu = 0.9345

iaccu = 99

最大限の精度は既定の精度よりやや高めです。したがって、最適なしきい値は、以下のようになります。

thre(iaccu)

ans = 0.5278

参考

TreeBagger | compact | oobError | mdsprox | oobMeanMargin | oobPredict | perfcurve | fitcensemble

関連するトピック

• TreeBagger の使用による回帰木の bootstrap aggregation (バギング)
• TreeBagger とバギング アンサンブルの比較
• 回帰 TreeBagger ワークフローに対する並列処理の使用

×

例を開く

この例の変更されたバージョンがあります。編集された方の例を開きますか?

いいえ、変更されたバージョンを上書きします。 はい