このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。

procrustes

プロクラステス解析

構文

d = procrustes(X,Y)

d = procrustes(X,Y,Name,Value)

[d,Z] = procrustes(___)

[d,Z,transform] = procrustes(___)

説明

d = procrustes(X,Y) は、ランドマーク点の構成で表される X と Y の形状間の 2 乗プロクラステス距離を返します。

d = procrustes(X,Y,Name,Value) では、1 つ以上の名前と値の引数を使用して追加オプションを指定します。たとえば、反射とスケーリングを無効にしてプロクラステス変換を制限できます。

[d,Z] = procrustes(___) は、前の構文におけるいずれかの入力引数の組み合わせを使用して、Y に対してプロクラステス変換を実行することで得られた形状 Z も返します。

[d,Z,transform] = procrustes(___) は、プロクラステス変換も返します。

例

プロクラステス距離の計算と重ね合わせた形状のプロット

2 つの形状のランドマーク点を含む行列を作成し、それらのランドマーク点をプロットして形状を可視化します。

X = [40 88; 51 88; 35 78; 36 75; 39 72; 44 71; 48 71; 52 74; 55 77];
Y = [36 43; 48 42; 31 26; 33 28; 37 30; 40 31; 45 30; 48 28; 51 24];
plot(X(:,1),X(:,2),"x")
hold on
plot(Y(:,1),Y(:,2),"o")
xlim([0 100])
ylim([0 100])
legend("Target shape (X)","Comparison shape (Y)")

形状を比較してそれらのプロクラステス距離を表示します。

[d,Z] = procrustes(X,Y)

d = 
0.2026

Z = 9×2

   39.7694   87.5089
   50.5616   86.8011
   35.5487   72.1631
   37.3131   73.9909
   40.8735   75.8503
   43.5517   76.7959
   48.0577   75.9771
   50.7835   74.2286
   53.5410   70.6841

Y を X に重ね合わせることで得られる形状を可視化します。

plot(Z(:,1),Z(:,2),"s")
legend("Target shape (X)","Comparison shape (Y)", ...
    "Transformed shape (Z)")
hold off

回転を含むプロクラステス変換の解析

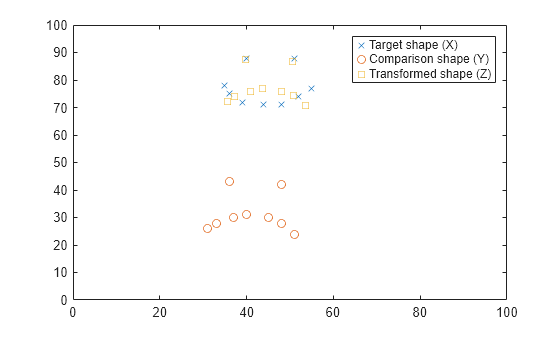
procrustes によって返されるプロクラステス変換を使用して、比較形状がターゲット形状にどのように重ね合わさるかを解析します。

2 次元の標本データを生成します。

rng("default")
n = 10;  
Y = normrnd(0,1,[n 2]);

Y を 60 度 (ラジアン単位で pi/3) 回転し、Y のサイズを係数 0.5 でスケーリングし、2 を追加して点を平行移動することで、ターゲット形状 X を作成します。また、X のランドマーク点にノイズを追加します。

S = [cos(pi/3) -sin(pi/3); sin(pi/3) cos(pi/3)]

S = 2×2

    0.5000   -0.8660
    0.8660    0.5000

X = normrnd(0.5*Y*S+2,0.05,n,2);

Y を X に変換できるプロクラステス変換を求めます。

[~,Z,transform] = procrustes(X,Y);

プロクラステス変換の成分を表示します。

transform

transform = struct with fields:
    T: [2×2 double]
    b: 0.4845
    c: [10×2 double]

transform.T

ans = 2×2

    0.4832   -0.8755
    0.8755    0.4832

transform.c

ans = 10×2

    2.0325    1.9836
    2.0325    1.9836
    2.0325    1.9836
    2.0325    1.9836
    2.0325    1.9836
    2.0325    1.9836
    2.0325    1.9836
    2.0325    1.9836
    2.0325    1.9836
    2.0325    1.9836

transform.T は行列 S に似ています。また、スケール成分 (transform.b) は 0.5 に近く、平行移動成分値 (transform.c) は 2 に近くなっています。

transform.T の行列式を計算して、transform.T が回転を示すか反射を示すかを判定します。回転行列の行列式は 1 で、反射行列の行列式は –1 です。

det(transform.T) 

ans = 
1

2 次元平面では、原点を中心に $\theta$ 度の角度だけ点を回転する回転行列は、次のような形式になります。

$\left[\begin{array}{cc}\cos \theta & -\sin \theta \\ \sin \theta & \cos \theta \end{array}\right]$.

$$\cos \theta$$ または $$\sin \theta$$ を使用する場合、回転角には –180 ～ 180 の範囲の値を 2 つ使用できます。$$\cos \theta$$ と $$\sin \theta$$ の両方の値を使用して、あいまいさがない行列の回転角を特定します。関数atan2dを使用して、$$\cos \theta$$ と $$\sin \theta$$ から $$\tan \theta$$ 値を特定できるほか、角度も特定できます。

theta = atan2d(transform.T(2,1),transform.T(1,1))

theta = 
61.1037

transform.T は 61 度の回転行列です。

反射を含むプロクラステス変換の解析

procrustes によって返されるプロクラステス変換を使用して、比較形状がターゲット形状にどのように重ね合わさるかを解析します。

2 つの異なる形状のランドマーク点をもつ行列を作成します。

X = [20 13; 20 20; 20, 29; 20 40; 12 36];
Y = [36 7; 36 10; 36 14; 36 20; 39 18];

ランドマーク点をプロットして形状を可視化します。

plot(X(:,1),X(:,2),"-x")
hold on
plot(Y(:,1),Y(:,2),"-o")
xlim([0 50])
ylim([0 50])
legend("Target shape (X)","Comparison shape (Y)")
hold off

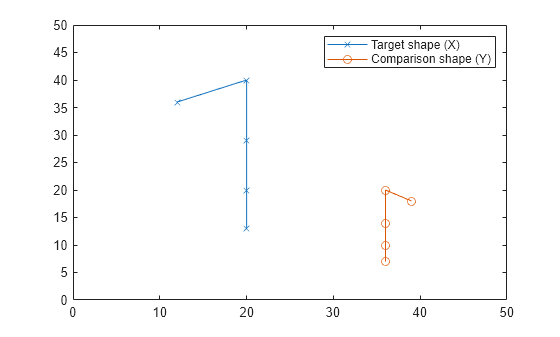
procrustes を使用してプロクラステス変換を取得します。

[d,Z,transform] = procrustes(X,Y)

d = 
0.0064

Z = 5×2

   20.1177   13.3935
   19.9145   19.6790
   19.6435   28.0597
   19.2371   40.6306
   13.0871   36.2371

transform = struct with fields:
    T: [2×2 double]
    b: 2.0963
    c: [5×2 double]

transform.T

ans = 2×2

   -0.9995   -0.0323
   -0.0323    0.9995

transform.c

ans = 5×2

   96.0177    1.1661
   96.0177    1.1661
   96.0177    1.1661
   96.0177    1.1661
   96.0177    1.1661

変換のスケール成分 b は、X のスケールが Y のスケールの約 2 倍であることを示しています。

変換の回転成分と反射成分の行列式を求めます。

det(transform.T)

ans = 
-1.0000

行列式は –1 です。つまり、変換に反射が含まれています。

2 次元平面では、反射行列は次のような形式になります。

$\left[\begin{array}{cc}\mathrm{cos2}\theta & \mathrm{sin2}\theta \\ \mathrm{sin2}\theta & -\mathrm{cos2}\theta \end{array}\right]$,

これは、"x" 軸と角度 $$\theta$$ をなす線に関する反射を示します。

$$\cos 2\theta$$ または $$\sin 2\theta$$ を使用する場合、反射線の角度には –90 ～ 90 の範囲の値を 2 つ使用できます。$$\cos 2\theta$$ と $$\sin 2\theta$$ の両方の値を使用して、あいまいさがない反射線の角度を特定します。関数atan2dを使用して、$$\cos 2\theta$$ と $$\sin 2\theta$$ から $$\tan 2\theta$$ 値を特定できるほか、角度も特定できます。

theta = atan2d(transform.T(2,1),transform.T(1,1))/2

theta = 
-89.0741

transform.T は、"x" 軸と約 –90 度の角度をなす線に関して点を鏡映します。この線は "y" 軸を示します。X と Y のプロットは、Y を X に重ね合わせるには "y" 軸に関する鏡映が必要であることを示しています。

数を増やした点集合へのプロクラステス変換の適用

ランドマーク点のプロクラステス変換を求め、その変換をランドマーク点よりも多い比較形状の点に適用します。

2 つの三角形 X (ターゲット形状) および Y (比較形状) のランドマーク点をもつ行列を作成します。

X = [5 0; 5 5; 8 5];
Y = [0 0; 1 0; 1 1];

三角形 Y の点の数を増やした行列を作成します。

Y_points = [linspace(Y(1,1),Y(2,1),10)' linspace(Y(1,2),Y(2,2),10)'
            linspace(Y(2,1),Y(3,1),10)' linspace(Y(2,2),Y(3,2),10)'
            linspace(Y(3,1),Y(1,1),10)' linspace(Y(3,2),Y(1,2),10)'];

数を増やした比較形状の点集合を含む両方の形状をプロットします。

plot([X(:,1); X(1,1)],[X(:,2); X(1,2)],"bx-")
hold on
plot([Y(:,1); Y(1,1)],[Y(:,2); Y(1,2)],"ro-","MarkerFaceColor","r")
plot(Y_points(:,1),Y_points(:,2),"ro")
xlim([-1 10])
ylim([-1 6])
legend("Target shape (X)","Comparison shape (Y)", ...
    "Additional points on Y","Location","northwest")

procrustes を呼び出して、比較形状からターゲット形状へのプロクラステス変換を取得します。

[d,Z,transform] = procrustes(X,Y)

d = 
0.0441

Z = 3×2

    5.0000    0.5000
    4.5000    4.5000
    8.5000    5.0000

transform = struct with fields:
    T: [2×2 double]
    b: 4.0311
    c: [3×2 double]

プロクラステス変換を使用して、比較形状の他の点 (Y_points) をターゲット形状に重ね合わせ、結果を可視化します。

Z_points = transform.b*Y_points*transform.T + transform.c(1,:);
plot([Z(:,1); Z(1,1)],[Z(:,2); Z(1,2)],"ks-","MarkerFaceColor","k")
plot(Z_points(:,1),Z_points(:,2),"ks")
legend("Target shape (X)","Comparison shape (Y)", ...
    "Additional points on Y","Transformed shape (Z)", ...
    "Transformed additional points","Location","best")
hold off

反射を行わない形状の比較

ランドマーク点を使用して手書き文字 d および b の形状を作成し、点をプロットして文字を可視化します。

D = [33 93; 33 87; 33 80; 31 72; 32 65; 32 58; 30 72;
     28 72; 25 69; 22 64; 23 59; 26 57; 30 57];
B = [48 83; 48 77; 48 70; 48 65; 49 59; 49 56; 50 66;
     52 66; 56 65; 58 61; 57 57; 54 56; 51 55];
plot(D(:,1),D(:,2),"x-")
hold on
plot(B(:,1),B(:,2),"o-")
legend("Target shape (d)","Comparison shape (b)")
hold off

procrustes を使用して反射をオフにした状態で文字を比較します。反射を行うと b が d になり、比較する形状が正確に保持されないためです。

d = procrustes(D,B,"reflection",false)

d = 
0.3425

反射をオンにした状態で procrustes を使用してみて、プロクラステス距離の違いを確認します。

d = procrustes(D,B,"reflection","best")

d = 
0.0204

b を反射すると d とうまく合致するため、この反射設定によりプロクラステス距離は小さくなります。

スケーリングを行わない形状の比較

ランドマーク点で表される 2 つの形状を作成し、点をプロットして可視化します。

X = [20 13; 20 20; 20 29; 20 40; 12 36];
Y = [36  7; 36 10; 36 14; 36 20; 39 18];
plot(X(:,1),X(:,2),"-x")
hold on
plot(Y(:,1),Y(:,2),"-o")
xlim([0 50])
ylim([0 50])
legend("Target shape (X)","Comparison shape (Y)")

プロクラステス解析を使用してスケーリングをオフにした状態で 2 つの形状を比較します。

[d,Z] = procrustes(X,Y,"scaling",false)

d = 
0.2781

Z = 5×2

   19.2194   20.8229
   19.1225   23.8214
   18.9932   27.8193
   18.7993   33.8162
   15.8655   31.7202

重ね合わせたランドマーク点を可視化します。

plot(Z(:,1),Z(:,2),"-s")
legend("Target shape (X)","Comparison shape (Y)", ...
    "Transformed shape (Z)")
hold off

重ね合わせた形状 Z のスケールは元の形状 Y と同じです。

入力引数

X — ターゲット形状

行列

ターゲット形状。n 行 p 列の行列として指定します。ここで、n の各行には p 次元のランドマーク点が含まれます。ランドマーク点は、比較のターゲットである形状を表します。

データ型: single | double

Y — 比較形状

行列

比較形状。n 行 q 列の行列として指定します。ここで、n の各行には q 次元 (q ≤ p) のランドマーク点が含まれます。ランドマーク点は、ターゲット形状と比較する形状を表します。

Y は X と同じ数の点 (行) をもっていなければなりません。ここで、Y の各点 Y(i,:) は X の同じ行の点 X(i,:) に対応します。

Y の点は、X の点よりも少ない次元 (列数) をもつことができます。その場合、procrustes は X の次元と一致するようにゼロの列を Y に追加します。

データ型: single | double

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで Name は引数名、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。

例: d = procrustes(X,Y,"Scaling",false,"reflection",false) は、変換でスケーリングも反射も行わずにプロクラステス解析を実行します。

Scaling — スケーリングを有効にするためのフラグ

true または 1 (既定値) | false または 0

プロクラステス変換でスケーリングを有効にするためのフラグ。logical 1 (true) または 0 (false) として指定します。値 false では、変換でスケーリングが行われません。値 true では、X と Y のランドマーク点の違いが最小化される場合にスケーリングを実行できます。

Scaling を false に設定すると、X のスケールと一致させるために Y をスケーリングすることなく、Y が X と比較されます。このオプションでは、スケールが異なる形状間のプロクラステス距離が大きくなります。

例: "Scaling",false

データ型: logical

Reflection — 反射を有効にするためのフラグ

"best" (既定値) | true または 1 | false または 0

プロクラステス変換で反射を有効にするためのフラグ。"best"、logical 1 (true)、または logical 0 (false) として指定します。

• "best" — 反射が含まれるかどうかに関係なく、最適なプロクラステス変換を求めます。

• 1 (true) — プロクラステス変換でランドマーク点の違いが最小化されるかどうかに関係なく、Y を強制的に鏡映します。

• 0 (false) — プロクラステス変換で Y を鏡映しません。このオプションでは、変換で回転は回避されません。

Reflection を false に設定すると、X の形状と一致させるために Y を鏡映することなく、Y が X と比較されます。このオプションでは、相互の反射である形状間のプロクラステス距離が大きくなります。

例: "Reflection",true

データ型: logical | string | char

出力引数

d — 2 乗プロクラステス距離

範囲 [0,1] の数値スカラー

2 つの形状間における非類似度の尺度である 2 乗プロクラステス距離。範囲 [0,1] の数値スカラーとして返されます。Scaling が false に設定されている場合、2 乗プロクラステス距離は [0,1] の範囲外になる可能性があります。

procrustes は、X と Z における対応する点の差の二乗和を使用してこの距離を計算します。その後、距離を X のスケールで標準化します。X のスケールは sum(sum((X-mean(X)).^2)) です。つまり、X の列の平均が 0 となる X の中心からの各要素の二乗和になります。

データ型: single | double

Z — 変換後の形状

数値行列

Y におけるランドマーク点の変換後の形状。X と同じサイズの n 行 p 列の数値行列として返されます。出力 Z は、Y にプロクラステス変換を適用した結果です。

データ型: single | double

transform — プロクラステス変換

構造体

プロクラステス変換。以下の 3 つのフィールドを含む構造体として返されます。

• T — 回転成分と反射成分。X のランドマーク点の向きと一致するように Y を回転または反射する p 行 p 列の変換行列で指定されます。

  • T が回転行列である場合、det(T) は 1 です。

  • T が反射行列である場合、det(T) は –1 です。

• b — スケール成分。X のスケールと一致するように Y のスケールを引き伸ばすか (b > 1)、保持するか (b = 1)、小さくする (b < 1) スカラーで指定されます。

• c — 変換成分。n 行 p 列の行列で指定されます。ここで、各行は X に移動するために Y の点に追加する p 次元のベクトルです。

プロクラステス変換では、次の変換を実行して Y を X に重ね合わせます。

Z = bYT + c.

transform.T に反射が確実に含まれないようにするには、名前と値の引数 Reflection を false に設定します。

スケール成分を削除し、transform.b を 1 に固定するには、名前と値の引数 Scaling を false に設定します。

データ型: struct

詳細

プロクラステス距離

プロクラステス距離は、プロクラステス解析に基づく形状間の非類似度の尺度です。

関数 procrustes は、X と Y の 2 つの形状間における最適な形状維持ユークリッド変換 (回転、反射、スケーリング、および平行移動で構成される) であるプロクラステス変換を求めます。プロクラステス変換は、X と Z におけるランドマーク点の差の二乗和を最小化する最適な変換です。ここで、Z は Y を X に重ね合わせることで得られる Y の変換後の形状です。

関数 procrustes は、2 乗プロクラステス距離 (d)、変換後の形状 (Z)、およびプロクラステス変換 (transform) を返します。2 乗プロクラステス距離は、X と Z の差の二乗和です。

ヒント

• プロクラステス解析は、X と Y のすべての次元が同様なスケールをもっている際に適切です。X と Y の列のスケールが異なる場合は、zscore または normalize を使用して列を標準化します。

• プロクラステス解析は多次元尺度構成法と併用できます。多次元尺度構成法を別個に適用することで、原則的に類似しているが、向きが違うために異なって見える再構成された点が生成される場合があります。また、再構成された点の向きは元の点とは異なる場合があります。関数 procrustes は点集合を変換して、他と比較しやすくします。例については、非空間的距離に適用した古典的多次元尺度構成法を参照してください。

参照

[1] Kendall, David G. “A Survey of the Statistical Theory of Shape.” Statistical Science. Vol. 4, No. 2, 1989, pp. 87–99.

[2] Bookstein, Fred L. Morphometric Tools for Landmark Data. Cambridge, UK: Cambridge University Press, 1991.

[3] Seber, G. A. F. Multivariate Observations. Hoboken, NJ: John Wiley & Sons, Inc., 1984.

バージョン履歴

R2006a より前に導入

参考

cmdscale | factoran

トピック

• プロクラステス解析の使用による手書き形状の比較