cmdscale
古典的多次元尺度構成法
説明
Y = cmdscale(D)n 行 n 列の距離行列または非類似度行列 D で古典的多次元尺度構成法を実行し、n 行 p 列の構成行列を返します。Y の行は p 次元空間の n 個の点の座標に対応し、p < n です。
D がユークリッド距離行列の場合、その要素は n 個の点間のペアワイズ距離であり、p はこれらの点を組み込むことができる最小空間の次元です。
D がユークリッド距離行列でない場合、または非類似度行列の場合、p は Y*Y' の正の固有値の数です。この場合、p へ低減する、または次元数を削減することは、Y*Y' の負の固有値の絶対値が小さい場合に限り、D の合理的な近似になります。
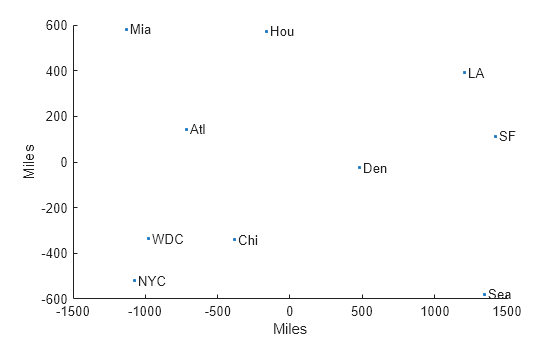
例
cmdscale 関数を使用して、米国の 10 都市間の地理的距離に基づく地図を作成します。
都市間のマイル単位の距離を格納する距離行列 D を作成します。D は完全な距離行列であるため、これは、対称な正方行列であり、対角要素がゼロで、非対角要素は正の値です。
cities = ... {"Atl","Chi","Den","Hou","LA","Mia","NYC","SF","Sea","WDC"}; D = [ 0 587 1212 701 1936 604 748 2139 2182 543; 587 0 920 940 1745 1188 713 1858 1737 597; 1212 920 0 879 831 1726 1631 949 1021 1494; 701 940 879 0 1374 968 1420 1645 1891 1220; 1936 1745 831 1374 0 2339 2451 347 959 2300; 604 1188 1726 968 2339 0 1092 2594 2734 923; 748 713 1631 1420 2451 1092 0 2571 2408 205; 2139 1858 949 1645 347 2594 2571 0 678 2442; 2182 1737 1021 1891 959 2734 2408 678 0 2329; 543 597 1494 1220 2300 923 205 2442 2329 0];
距離行列を cmdscale 関数に渡して、構成行列と固有値を取得します。
[Y,e] = cmdscale(D)
Y = 10×6
103 ×
-0.7188 0.1430 0.0351 -0.0012 -0.0074 0.0015
-0.3821 -0.3408 0.0296 -0.0082 -0.0120 -0.0023
0.4816 -0.0253 0.0534 0.0013 0.0157 -0.0010
-0.1615 0.5728 0.0015 -0.0018 -0.0007 0.0027
1.2037 0.3901 -0.0186 0.0150 -0.0032 -0.0017
-1.1335 0.5819 -0.0323 -0.0024 0.0030 -0.0020
-1.0722 -0.5190 -0.0343 -0.0143 0.0064 0.0003
1.4206 0.1126 -0.0078 -0.0181 -0.0008 0.0009
1.3417 -0.5797 -0.0237 0.0060 -0.0014 0.0006
-0.9796 -0.3355 -0.0029 0.0237 0.0004 0.0010
e = 10×1
106 ×
9.5821
1.6868
0.0082
0.0014
0.0005
0.0000
0.0000
-0.0009
-0.0055
-0.0355
正の固有値が 6 つしかないので、構成行列 Y は 10 行 6 列です。いくつかの固有値は負で、元の距離がユークリッドではないことを示します。この結果になるのは、地表が曲面であるためです。
2 つの最大の正の固有値は、大きさにおいて、その他の固有値よりはるかに大きいです。したがって、負の固有値があるにもかかわらず、Y の最初の 2 つの座標は D の合理的な近似に十分です。
D と 2 つの最大固有値を使用する近似の最大相対誤差を計算します。
Dapprox = squareform(pdist(Y(:,1:2))); MaxRelDiff = max(abs(D-Dapprox),[],"all")/max(D,[],"all")
MaxRelDiff = 0.0075
距離行列の再構成により、元の距離行列の適切な近似が得られます。
地図として再構成された都市の位置をプロットします。D には都市間の距離に関する情報のみが含まれているため、再構成の地理的方位は任意です。
scatter(Y(:,1),Y(:,2),".") text(Y(:,1)+25,Y(:,2),cities) xlabel("Miles") ylabel("Miles")
Copyright 2012–2024 The MathWorks, Inc.
異なる尺度を使用することにより距離に対して点を次元削減すると距離行列の近似の品質がどのように変化するかを調べます。
3 次元空間に近い 4 次元空間の点を 10 個無作為に生成します。座標軸には沿っていない 3 次元部分空間に変換後の値が近づくように、点に線形変換を適用します。
rng(0,"twister"); % For reproducibility A = [normrnd(0,1,10,3),normrnd(0,0.1,10,1)]; B = randn(4,4); X = A*B;
既定のユークリッド尺度を使用して、X 内の点の距離行列を作成します。
D = pdist(X);
cmdscale 関数を使用して、点間の距離から構成行列 Y を作成します。
Y = cmdscale(D);
2、3 または 4 次元を使用した場合について、再構成の品質を比較します。
maxerr2 = max(abs(pdist(X)-pdist(Y(:,1:2))))
maxerr2 = 0.1631
maxerr3 = max(abs(pdist(X)-pdist(Y(:,1:3))))
maxerr3 = 0.0187
maxerr4 = max(abs(pdist(X)-pdist(Y)))
maxerr4 = 1.1768e-14
maxerr3 の値が小さいので、はじめの 3 つの次元により距離行列の適切な再構成が行われることがわかります。
cityblock 尺度を使用して、X 内の点の距離行列を作成します。
D = pdist(X,"cityblock"); 点間の距離から構成行列 Y を作成し、固有値を取得します。
[Y,e] = cmdscale(D)
Y = 10×6
-6.0490 0.7237 0.0722 -0.5919 0.3802 0.1243
11.3882 -0.0401 2.0088 0.0420 -0.0079 -0.1248
-9.6056 -0.8110 -0.0974 0.7589 0.2705 0.0341
-2.3302 1.9110 0.1458 0.3004 -0.2000 -0.0681
-0.5196 -0.2462 0.0621 -0.0654 0.6354 -0.0340
-9.7676 0.0801 -0.0075 -0.4611 -0.3454 0.0470
-6.1074 -0.2389 0.0042 0.1992 -0.4226 -0.1820
1.8210 -1.7431 -0.0503 -0.2991 -0.2408 0.0089
10.9626 0.1941 -1.5058 -0.0541 0.0600 -0.4369
10.2077 0.1703 -0.6322 0.1712 -0.1295 0.6315
e = 10×1
624.6469
8.0643
6.7448
1.3965
1.0377
0.6631
-0.0000
-0.0685
-0.6633
-5.6586
最大相対誤差を計算して、再構成の品質を評価します。
maxerr = max(abs(D-pdist(Y,"cityblock")))/max(D)maxerr = 0.2019
固有値の 1 つが絶対値の大きい負の値なので、再構成の品質は相対的に低い可能性があります。
入力引数
出力引数
参照
[1] Cox, Trevor F., and Michael A. A. Cox. Multidimensional Scaling. 2nd ed. Monographs on Statistics and Applied Probability 88. Boca Raton: Chapman & Hall/CRC, 2001.
[2] Davison, Mark L. Multidimensional Scaling. Wiley Series in Probability and Mathematical Statistics. New York: Wiley, 1983.
[3] Seber, G. A. F. Multivariate Observations. 1st ed. Wiley Series in Probability and Statistics. Wiley, 1984.
バージョン履歴
R2006a より前に導入
