非古典的および非計量多次元尺度構成法

mdscale を使用して非古典的多次元尺度構成法を実行します。

非古典的多次元尺度構成法

関数 mdscale は、非古典的多次元尺度構成法を実行します。cmdscale と同様に、"位置" が存在しない非類似度データを可視化するか、その次元を削減させることによって高次元のデータを可視化するには mdscale を使用します。両方の関数は、入力として非類似度行列を取り、点の配置を作成します。しかし、mdscale は、欠損データと重みを取り、さまざまな基準の選択を提供して配置を作成します。

たとえば、シリアルのデータは、朝食のシリアルについて 10 個の変数を含みます。mdscale を使用して、これらのデータを 2 次元で可視化できます。まず、データを読み込みます。念のため、この例では、22 個のサブセットの観測からなることを確認します。

load cereal.mat
X = [Calories Protein Fat Sodium Fiber ... 
    Carbo Sugars Shelf Potass Vitamins];
% Take a subset from a single manufacturer
mfg1 = strcmp('G',cellstr(Mfg));
X = X(mfg1,:);
size(X)

ans =
    22 10

次に、pdist を使用して 10 次元のデータを非類似度に変換します。pdist からの出力は、上三角に (23*22/2) 個の要素から成る対称非類似度行列であり、それらがベクトルとして格納されます。

dissimilarities = pdist(zscore(X),'cityblock');
size(dissimilarities)

ans =
     1   231

この例のコードは、最初にシリアルのデータを標準化してから非類似度として市街地距離を利用します。非類似度への変換の選択は、目的に依存します。ここでは簡単な例として選択しています。目的によっては、元のデータが既に非類似度の形式である場合があります。

次に、mdscale を使用して計量的 MDS を実行します。cmdscale とは違って、適切な次元数と、出力の配置を構成するために使用するメソッドを指定しなければなりません。この例の場合、2 次元を使用します。計量的 STRESS の基準は、出力を計算するための一般的な方法です。他の選択肢については、オンライン ドキュメンテーションの mdscale のリファレンス ページを参照してください。mdscale からの 2 番目の出力は、出力の配置の評価に使われた基準の値です。これは、出力の配置の点間の距離が、オリジナルの入力の非類似度をどれほど適切に近似するかを測ります。

[Y,stress] =... 
mdscale(dissimilarities,2,'criterion','metricstress');
stress

stress =
    0.1856

mdscale からの出力プロットは、オリジナルの 10 次元のデータを 2 次元で表し、関数 gname を使用して選択した点のラベルを表示します。

plot(Y(:,1),Y(:,2),'o','LineWidth',2);
gname(Name(mfg1))

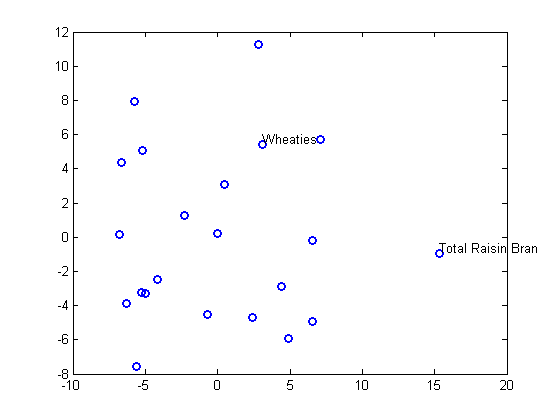
非計量多次元尺度構成法

計量多次元尺度構成法は、その点間の距離が与えられた非類似度を近似するように点の配置を作成します。これは厳しすぎる要求で、非計量多次元尺度構成法はこれを少し緩和するように設計されています。非計量多次元尺度構成法では、非類似度自身を近似せずに、非類似度を、非線形であっても単調になるように変換してから近似します。単調性があるので、出力のプロットの距離が大きい (小さい) ほど、より大きい (小さい) 類似度に相当します。ただし、非線形性は mdscale が非類似度の順序の保存のみを試みることを意味します。したがって、異なる尺度での、距離の縮小または拡大があるかもしれません。

mdscale を使用すると、計量多次元尺度構成法とほぼ同じ方法で非計量 MDSを実行します。非計量的 STRESS 基準は、出力を計算するための一般的な方法です。他の選択肢については、オンライン ドキュメンテーションの mdscale のリファレンス ページを参照してください。計量多次元尺度構成法と同様に、mdscale からの 2 番目の出力は、出力の配置に対して評価された、その基準の値です。ただし、非計量多次元尺度構成法の場合、出力の配置の点間の距離が非類似度をどれほどよく近似するかを測定します。3 番目の出力には、非類似度が返されます。これらは、オリジナルの非類似度を変換した値です。

[Y,stress,disparities] = ... 
mdscale(dissimilarities,2,'criterion','stress');
stress

stress =
    0.1562

非類似度に対する出力構成の適合性を確認し、格差を理解するには、Shepard プロットを作成すると便利です。

distances = pdist(Y);
[dum,ord] = sortrows([disparities(:) dissimilarities(:)]);
plot(dissimilarities,distances,'bo', ...
     dissimilarities(ord),disparities(ord),'r.-', ...
     [0 25],[0 25],'k-')
xlabel('Dissimilarities')
ylabel('Distances/Disparities')
legend({'Distances' 'Disparities' '1:1 Line'},...
       'Location','NorthWest');

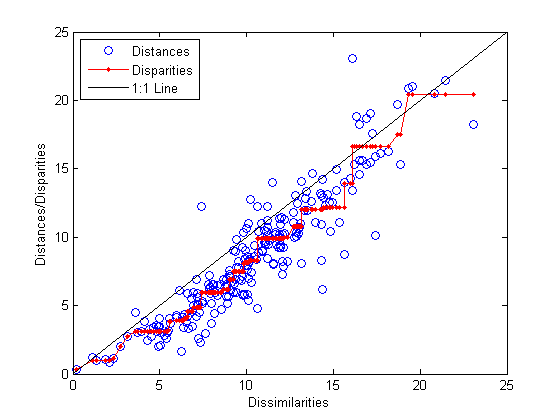
このプロットは、mdscale が、点間の距離が非類似度を近似する 2 次元の点の配置を見つけたことを示します。これは、オリジナルの非類似度の非線形変換と言えます。この不一致が非類似度の関数として凹形状であることは、近似によって、対応する非類似度に比べて点間の間隔が少し縮められる傾向にあることを示します。これは、実際に許容できるものです。

mdscale は、反復アルゴリズムを使用して出力の配置を見つけます。その結果は、しばしば開始点に依存することがあります。既定の設定では、mdscale は、cmdscale を使用して初期の配置を構成し、この選択によって大域的に最適解になることがあります。しかし、mdscale は、基準が局所的に最小となる配置で停止することもあります。このような場合は、別の開始点を使って mdscale を複数回実行することになります。これは、名前と値のペアの引数 'start' および 'replicates' を使用して行うことができます。以下のコードは、MDS を 5 回繰り返し実行します。それぞれは、別々に無作為に選択された初期配置で始めます。この基準値は、各繰り返しに対して表示されます。このとき mdscale は、最適近似をもつ配置を返します。

opts = statset('Display','final');
[Y,stress] =... 
mdscale(dissimilarities,2,'criterion','stress',... 
'start','random','replicates',5,'Options',opts);

35 iterations, Final stress criterion = 0.156209
31 iterations, Final stress criterion = 0.156209
48 iterations, Final stress criterion = 0.171209
33 iterations, Final stress criterion = 0.175341
32 iterations, Final stress criterion = 0.185881

mdscale は、いくつかの異なる局所解を探すことに注意してください。これらのいくつかは、cmdscale の開始点として見つけられた解ほど低い stress の値をもちません。

参考

mdscale | pdist | gname