このページの内容は最新ではありません。最新版の英語を参照するには、ここをクリックします。
mdscale
非古典的多次元尺度構成法
構文
説明
Y = mdscale(___,Name=Value)
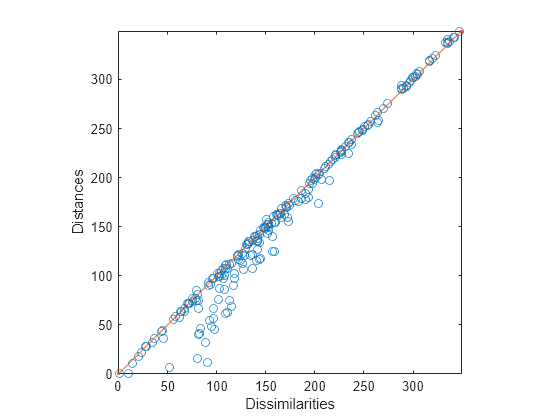
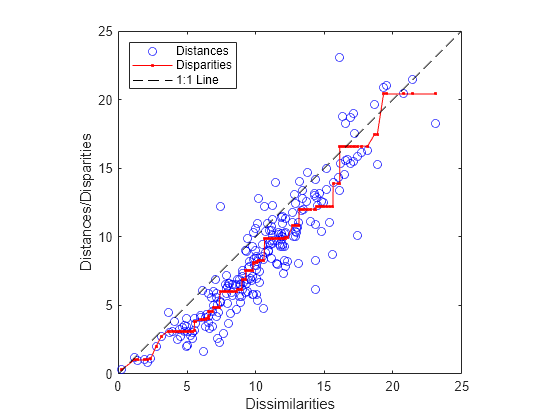
[ は、格差を追加で返します。これは、Y,stress,disparities]= mdscale(___)D の非類似度の単調変換です。
例
同じデータ セットで非計量多次元尺度構成法と計量多次元尺度構成法を実行します。
77 種類のシリアルの栄養情報が格納された cereal データ セットを読み込みます。
load cereal単一の製造元のシリアルの選択した測定値で構成されるデータのサブセットを取得します。
X = [Calories,Protein,Fat,Sodium,Fiber, ... Carbo,Sugars,Shelf,Potass,Vitamins]; X = X(strcmp("K",cellstr(Mfg)),:); size(X)
ans = 1×2
23 10
X には 23 個の観測値と 10 個の予測子変数が含まれています。
pdist 関数を使用して非類似度行列を作成します。
dissimilarities = pdist(X)
dissimilarities = 1×253
122.2784 322.6329 288.6226 347.3615 204.0662 295.9206 322.6050 303.9539 342.0409 141.1241 288.2603 263.6001 214.4808 293.1996 206.9734 248.1290 293.2388 107.3126 334.9910 289.9034 340.9883 269.9685 306.9267 335.2238 320.2312 180.7291 316.7823 306.8843 317.1183 274.2408 186.4457 288.6451 264.9925 203.6566 303.0380 234.1880 245.6135 349.3895 134.7739 264.2593 336.9481 304.9607 295.9307 166.1174 36.5240 131.1297 96.1613 1.4142 75.2994 143.8332
size(squareform(dissimilarities))
ans = 1×2
23 23
dissimilarities は、非類似度行列の 253 個の上三角要素を含む 23 行 23 列のサイズの行ベクトルになります。
非計量多次元尺度構成法を使用してデータを 2 次元で再作成します。
[Y,~,disparities] = mdscale(dissimilarities,2); distances = pdist(Y);
Shepard プロットを使用して結果を可視化します。
[~,ord] = sortrows([disparities(:),dissimilarities(:)]); plot(dissimilarities,distances,"o", ... dissimilarities(ord),disparities(ord),".-"); axis square xlim([0 max(dissimilarities)]); ylim([0 max(dissimilarities)]); xlabel("Dissimilarities") ylabel("Distances/Disparities") legend(["Distances","Disparities"],Location="northwest");
青い円の x 座標はそれらの元の非類似度の値に対応し、y 座標はそれらの 2 次元空間でのユークリッド距離に対応します。ほとんどの点が 1:1 線の近くにあり、2 次元尺度構成法によって、それよりも高次元の非類似度のある程度適切な表現が得られることを示しています。連結された赤い点は格差の値を示します。これは、非類似度の単調変換です。
同じ非類似度で metricsstress の基準を使用して計量多次元尺度構成法を実行します。
[Y,stress] = mdscale(dissimilarities,2,Criterion="metricsstress");
distances = pdist(Y);Shepard プロットを使用して結果を可視化します。計量多次元尺度構成法には非類似度がないため、赤い 1:1 線をプロットします。
plot(dissimilarities,distances,"o", ... [0 max(dissimilarities)],[0 max(dissimilarities)],".-") %xlim([0 max(dissimilarities)]); axis square; xlim([0 max(dissimilarities)]); ylim([0 max(dissimilarities)]); xlabel("Dissimilarities") ylabel("Distances")
ほとんどの点が 1:1 線の非常に近くにあり、2 次元尺度構成法によって、それよりも高次元の非類似度の適切な表現が得られることを示しています。
この例では、mdscale を使用して非計量多次元尺度構成法を実行する方法を示します。
計量多次元尺度構成法 (MDS) は、その点間の距離が与えられた非類似度を近似するように点の構成を作成します。これは要件が厳しすぎることがあり、非計量多次元尺度構成法はそれより厳しくない代替方法となります。非計量多次元尺度構成法では、非類似度自身を近似せずに、非類似度を、非線形であっても単調になるように変換してから近似します。単調性があるので、出力のプロットの距離が大きい (小さい) ほど、より大きい (小さい) 非類似度に相当します。ただし、非線形性は mdscale が非類似度の順序の保存のみを試みることを意味します。したがって、異なる尺度での、距離の縮小または拡大があるかもしれません。
cereal データ セットを読み込みます。これには、77 種類の朝食のシリアルについて記述する 10 個の変数の測定値が含まれています。
rng(0,"twister"); % For reproducibility load cereal
単一の製造元のシリアルの選択した測定値で構成されるデータのサブセットを取得します。
X = [Calories Protein Fat Sodium Fiber ... Carbo Sugars Shelf Potass Vitamins]; X = X(strcmp("G",cellstr(Mfg)),:); size(X)
ans = 1×2
22 10
X には 22 個の観測値と 10 個の予測子変数が含まれています。
pdistを使用して 10 次元のデータを非類似度に変換します。最初にシリアルのデータを標準化し、市街地距離を非類似度として使用します。
dissimilarities = pdist(zscore(X),'cityblock');
size(dissimilarities)ans = 1×2
1 231
pdist からの出力は対称な非類似度行列であり、(22*21/2) 個の要素を上三角にのみ含むベクトルとして格納されます。非類似度への変換の選択は目的に依存します。ここでは簡単にするためだけに行っています。目的によっては、元のデータが既に非類似度の形式である場合があります。
mdscale を使用して、クラスカルのストレス式 1 のモデルで非計量多次元尺度構成法を実行します。
[Y,stress,disparities] = mdscale(dissimilarities,2,Criterion="stress");
stressstress = 0.1562
非計量的 stress 基準は、出力を計算するための一般的な方法です。他の選択肢については、オンライン ドキュメンテーションの mdscale のリファレンス ページを参照してください。mdscale からの 2 番目の出力は、出力の配置の評価に使われた基準の値です。出力構成の点間の距離が格差をどの程度近似するかを示す尺度になります。3 番目の出力には、格差が返されます。これらは、元の非類似度を単調変換した値です。
それらのデータを可視化して、非類似度に対する出力構成の適合性を確認し、格差を理解します。
distances = pdist(Y); [dum,ord] = sortrows([disparities(:) dissimilarities(:)]); plot(dissimilarities,distances,"bo",dissimilarities(ord),... disparities(ord),"r.-",[0 25],[0 25],"k--") axis square; xlabel("Dissimilarities") ylabel("Distances/Disparities") legend({"Distances" "Disparities" "1:1 Line"},... "Location","NorthWest");
mdscale は、点間の距離が格差を近似する 2 次元の点の構成を見つけます。これは、元の非類似度の非線形変換と言えます。この不一致が非類似度の関数として格差の凹形状であることは、近似によって、対応する非類似度に比べて点間の間隔が少し縮められる傾向にあることを示します。これは、実際には十分に許容可能と思われます。
mdscale は、反復アルゴリズムを使用して出力の配置を見つけます。その結果は、しばしば開始点に依存することがあります。既定では、mdscale はcmdscaleを使用して初期構成を作成し、この選択によって多くの場合はグローバルな最適解が得られます。しかし、mdscale は、基準のローカルな最小値となる構成を返すこともあります。このような場合は、別の開始点を使って mdscale を複数回実行することになります。これは、名前と値の引数 Start および Replicates を使用して行うことができます。
スケーリングを繰り返します。今回は MDS の 5 つの複製を使用し、それぞれを無作為に選択された異なる初期構成で始めます。mdscale は、各反復の最終的なストレスの基準を表示し、最も良く適合する構成を返します。
[Y,stress] = mdscale(dissimilarities,2,Criterion="stress",... Start="random",Replicates=5, ... Options=statset(Display="final"));
35 iterations, Final stress criterion = 0.156209 31 iterations, Final stress criterion = 0.156209 48 iterations, Final stress criterion = 0.171209 33 iterations, Final stress criterion = 0.175341 32 iterations, Final stress criterion = 0.185881
mdscale は、いくつかの異なるローカル解を探すことに注意してください。これらのいくつかは、cmdscale の開始点として見つけられた解ほど低い stress の値をもちません。
入力引数
名前と値の引数
出力引数
参照
[1] Cox, Trevor F., and Michael A. A. Cox. Multidimensional Scaling. 2nd ed. Monographs on Statistics and Applied Probability 88. Boca Raton: Chapman & Hall/CRC, 2001.
[2] Davison, Mark L. Multidimensional Scaling. Wiley Series in Probability and Mathematical Statistics. New York: Wiley, 1983.
[3] Kruskal, J. B. “Multidimensional Scaling by Optimizing Goodness of Fit to a Nonmetric Hypothesis.” Psychometrika 29, no. 1 (March 1964): 1–27.
[4] Kruskal, J. B. “Nonmetric Multidimensional Scaling: A Numerical Method.” Psychometrika 29, no. 2 (June 1964): 115–29. https://doi.org/10.1007/BF02289694.
[5] Sammon, J.W. “A Nonlinear Mapping for Data Structure Analysis.” IEEE Transactions on Computers C–18, no. 5 (May 1969): 401–9.
[6] Seber, G. A. F. Multivariate Observations. 1st ed. Wiley Series in Probability and Statistics. Wiley, 1984.
バージョン履歴
R2006a より前に導入
