プロクラステス解析の使用による手書き形状の比較

この例では、プロクラステス解析を使用して 2 つの手書き数字 3 を比較する方法を示します。サイズと反射の変更を強制する効果を視覚的および解析的に調べます。

オリジナル データの読み込みと表示

2 つの手書き数字 3 についてのランドマーク データを入力します。

A = [11 39;17 42;25 42;25 40;23 36;19 35;30 34;35 29;...
30 20;18 19];
B = [15 31;20 37;30 40;29 35;25 29;29 31;31 31;35 20;...
29 10;25 18];

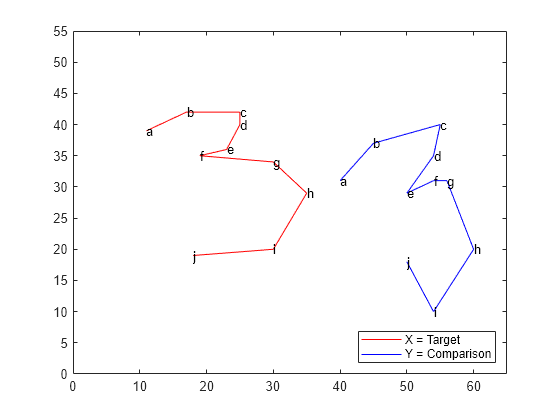
A と B から X と Y を作成します。各形状を見やすくするため、B を横に移動します。

X = A;
Y = B + repmat([25 0], 10,1);

文字を使用してランドマーク点を示し、形状をプロットします。図の線は点をつなぎ、各形状の図面パスを示します。

plot(X(:,1), X(:,2),'r-', Y(:,1), Y(:,2),'b-');
text(X(:,1), X(:,2),('abcdefghij')')
text(Y(:,1), Y(:,2),('abcdefghij')')
legend('X = Target','Y = Comparison','location','SE')
xlim([0 65]);
ylim([0 55]);

最良の変換を計算

プロクラステス解析を使用して、ランドマーク データ点同士の距離を最小化する変換を見つけます。

[d,Z,tr] = procrustes(X,Y);

この関数は、d (標準化した非類似度の尺度)、Z (変換したランドマークの行列) および tr (変換方程式に対応するフィールド T 、b および c がある、計算した変換の構造体配列) を出力します。

青い破線を使用して、変換した形状 Z を可視化します。

plot(X(:,1), X(:,2),'r-', Y(:,1), Y(:,2),'b-',...
Z(:,1),Z(:,2),'b:');
text(X(:,1), X(:,2),('abcdefghij')')
text(Y(:,1), Y(:,2),('abcdefghij')')
text(Z(:,1), Z(:,2),('abcdefghij')')
legend('X = Target','Y = Comparison',...
'Z = Transformed','location','SW')
xlim([0 65]);
ylim([0 55]);

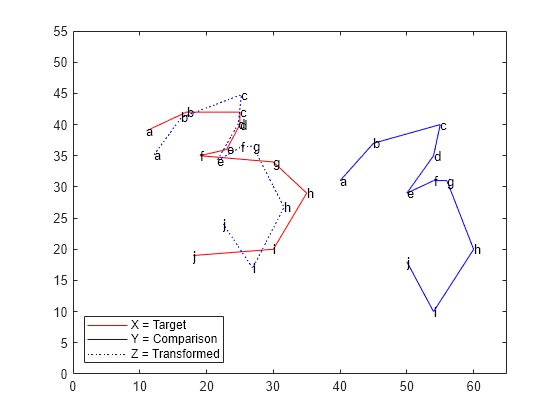
2 つの形状の相似を検査

非類似度の尺度 d およびスケーリング尺度 b という 2 つの異なる数値を使用して、ターゲットの形状と変換した形状の類似度を評価します。

非類似度の測定値 d は 0 ～ 1 の数を与え、ターゲットの形状と変換済みの形状の差異を表します。0 付近の値は類似した形状を示し、1 付近の値は非類似度を示します。

d

d = 0.1502

この例では d の値が小さいので、2 つの形状が似ていることがわかります。procrustes は、列平均に対する元の点の偏差の二乗和と点集合間の偏差の二乗和を比較することにより d を計算します。

numerator = sum(sum((X-Z).^2))

numerator = 166.5321

denominator = sum(sum((X-mean(X)).^2))

denominator = 1.1085e+03

ratio = numerator/denominator

ratio = 0.1502

得られた尺度 d は、形状のサイズのスケールとは関係なく、ランドマーク データの類似度のみを対象にします。

形状のサイズの類似度を調べます。

tr.b

ans = 0.9291

前の図では、ターゲット形状と比較形状のサイズは同じように見えます。この視覚的な印象は、b = % 0.93 という値によって補強されます。これは、最良の変換により比較形状のサイズが .93 倍 (わずか 7% の縮小) になることを示します。

変換の形式を制限

スケーリングと反射係数を手動で調整する効果を探究します。

b を強制的に 1 に設定 ('Scaling' を false に設定) し、ターゲットの図と変換した図におけるサイズの非類似度を調べます。

ds = procrustes(X,Y,'Scaling',false)

ds = 0.1552

この場合、'Scaling' を false に設定しても、d の計算値は 0.0049 しか大きくなりません。これはさらに 2 つの数字 3 のサイズの相似を立証します。d をさらに増加すると、より大きいサイズが一致しなくなります。

この例は、形状の位置を合わせるために、反射ではなく回転のみを必要とします。これは、この分析における行列 T の行列式が 1 であることからわかります。

det(tr.T)

ans = 1.0000

変換に反射が必要な場合は、T の行列式は -1 です。次のようにすると、反射を強制的に変換に組み込むことができます。

[dr,Zr,trr] = procrustes(X,Y,'Reflection',true);
dr

dr = 0.8130

d の値が大幅に大きくなるので、強制的に反射を行うとランドマーク点の変換が適切ではなくなることがわかります。変換した形状のプロットは、同様の結果を示します。

plot(X(:,1), X(:,2),'r-', Y(:,1), Y(:,2),'b-',...
Zr(:,1),Zr(:,2),'b:');
text(X(:,1), X(:,2),('abcdefghij')')
text(Y(:,1), Y(:,2),('abcdefghij')')
text(Zr(:,1), Zr(:,2),('abcdefghij')')
legend('X = Target','Y = Comparison',...
'Z = Transformed','Location','SW')
xlim([0 65]);
ylim([0 55]);

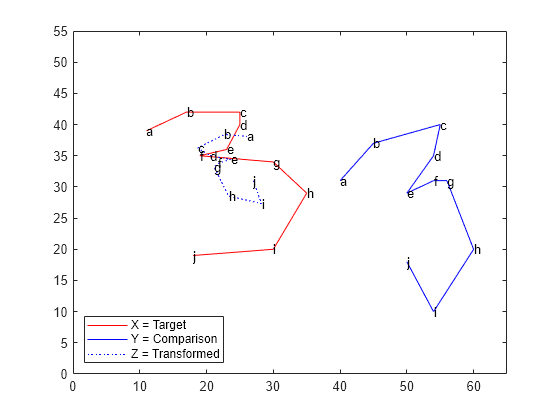
ランドマーク データ点はターゲットの対応点からさらに離れてしまいます。変換した 3 は不適当な鏡像のターゲット 3 になります。

変換した形状を上下逆にすると、より一致するかもしれません。しかし、形状を上下逆にすると、ランドマーク データ点がターゲットの対応点から離れてしまうため、変換はさらに悪くなります。この例から、一般的にスケーリングと反射のパラメーターの手動調整が最適ではないことが明らかになります。

参考

procrustes