factoran

因子分析

構文

lambda = factoran(X,m)

[lambda,psi] = factoran(X,m)

[lambda,psi,T] = factoran(X,m)

[lambda,psi,T,stats] = factoran(X,m)

[lambda,psi,T,stats,F] = factoran(X,m)

___ = factoran(X,m,Name,Value)

説明

factoran は、因子分析モデルの因子負荷量行列 Λ の最尤推定 (MLE) を計算します。

$$x=\mu +\Lambda f+e$$

ここで、x は観測変数のベクトル、μ は平均の定数ベクトル、Λ は因子負荷量の d 行 m 列の定数行列、f は標準化した独立共通因子のベクトル、e は独立した特殊因子のベクトルです。x、μ、および e の長さは d です。f の長さは m です。

あるいは、因子分析モデルは次のように指定することができます。

$$\mathrm{cov}(x)=\Lambda {\Lambda }^T+\Psi$$

ここで、$$\Psi =\mathrm{cov}(e)$$ は独自因子の分散から構成される d 行 d 列の対角行列です。

factoran の使用、およびその pca との関連性については、試験の成績に対する因子分析の実行を参照してください。

lambda = factoran(X,m) は、m 個の共通因子をもつデータ行列 X の因子負荷量行列 lambda を返します。

[lambda,psi] = factoran(X,m) は、独自因子の分散から構成される最尤推定量も返します。

[lambda,psi,T] = factoran(X,m) は、m 行 m 列の因子負荷量回転行列 T を返します。

[lambda,psi,T,stats] = factoran(X,m) は、共通因子の数が m であるという帰無仮説 H₀ に関連する情報を含む構造体 stats も返します。

[lambda,psi,T,stats,F] = factoran(X,m) は、共通因子の予測値 (因子スコア) も返します。

___ = factoran(X,m,Name,Value) は、前の構文の出力引数について、1 つ以上の名前と値のペアの引数を使用して、モデルの当てはめと出力を変更します。たとえば、X のデータが共分散行列であると指定できます。

例

人為的なデータの因子分析

いくつかの疑似ランダム生データを作成します。

rng default % For reproducibility
n = 100;
X1 = 5 + 3*rand(n,1); % Factor 1
X2 = 20 - 5*rand(n,1); % Factor 2

生データから 6 つのデータ ベクトルを作成し、ランダム ノイズを追加します。

Y1 = 2*X1 + 3*X2 + randn(n,1);
Y2 = 4*X1 + X2 + 2*randn(n,1);
Y3 = X1 - X2 + 3*randn(n,1);
Y4 = -2*X1 + 4*X2 + 4*randn(n,1);
Y5 = 3*(X1 + X2) + 5*randn(n,1);
Y6 = X1 - X2/2 + 6*randn(n,1);

データ ベクトルからデータ行列を作成します。

X = [Y1,Y2,Y3,Y4,Y5,Y6];

factoran を使用してノイズのあるデータ行列 X から 2 つの因子を抽出します。出力を表示します。

m = 2;
[lambda,psi,T,stats,F] = factoran(X,m);
disp(lambda)

    0.8666    0.4828
    0.8688   -0.0998
   -0.0131   -0.5412
    0.2150    0.8458
    0.7040    0.2678
   -0.0806   -0.2883

disp(psi)

    0.0159
    0.2352
    0.7070
    0.2385
    0.4327
    0.9104

disp(T)

    0.8728    0.4880
    0.4880   -0.8728

disp(stats)

    loglike: -0.0531
        dfe: 4
      chisq: 5.0335
          p: 0.2839

disp(F(1:10,:))

    1.8845   -0.6568
   -0.1714   -0.8113
   -1.0534    2.0743
    1.0390   -1.1784
    0.4309    0.9907
   -1.1823    0.6570
   -0.2129    1.1898
   -0.0844   -0.7421
    0.5854   -1.1379
    0.8279   -1.9624

データの相関行列を表示します。

corrX = corr(X)

corrX = 6×6

    1.0000    0.7047   -0.2710    0.5947    0.7391   -0.2126
    0.7047    1.0000    0.0203    0.1032    0.5876    0.0289
   -0.2710    0.0203    1.0000   -0.4793   -0.1495    0.1450
    0.5947    0.1032   -0.4793    1.0000    0.3752   -0.2134
    0.7391    0.5876   -0.1495    0.3752    1.0000   -0.2030
   -0.2126    0.0289    0.1450   -0.2134   -0.2030    1.0000

corrX を、factoran によって返された対応する値 lambda*lambda' + diag(psi) と比較します。

C0 = lambda*lambda' + diag(psi)

C0 = 6×6

    1.0000    0.7047   -0.2726    0.5946    0.7394   -0.2091
    0.7047    1.0000    0.0426    0.1023    0.5849   -0.0413
   -0.2726    0.0426    1.0000   -0.4605   -0.1542    0.1571
    0.5946    0.1023   -0.4605    1.0000    0.3779   -0.2611
    0.7394    0.5849   -0.1542    0.3779    1.0000   -0.1340
   -0.2091   -0.0413    0.1571   -0.2611   -0.1340    1.0000

factoran は、元のデータの相関行列に密接に対応する lambda と psi を取得します。

回転を使用せずに結果を表示します。

[lambda,psi,T,stats,F] = factoran(X,m,'Rotate','none');
disp(lambda)

    0.9920    0.0015
    0.7096    0.5111
   -0.2755    0.4659
    0.6004   -0.6333
    0.7452    0.1098
   -0.2111    0.2123

disp(psi)

    0.0159
    0.2352
    0.7070
    0.2385
    0.4327
    0.9104

disp(T)

     1     0
     0     1

disp(stats)

    loglike: -0.0531
        dfe: 4
      chisq: 5.0335
          p: 0.2839

disp(F(1:10,:))

    1.3243    1.4929
   -0.5456    0.6245
    0.0928   -2.3246
    0.3318    1.5356
    0.8596   -0.6544
   -0.7114   -1.1504
    0.3947   -1.1424
   -0.4358    0.6065
   -0.0444    1.2789
   -0.2350    2.1169

X の共分散行列のみを使用して因子を計算します。

X2 = cov(X);
[lambda2,psi2,T2,stats2] = factoran(X2,m,'Xtype','covariance','Nobs',n)

lambda2 = 6×2

    0.8666    0.4828
    0.8688   -0.0998
   -0.0131   -0.5412
    0.2150    0.8458
    0.7040    0.2678
   -0.0806   -0.2883

psi2 = 6×1

    0.0159
    0.2352
    0.7070
    0.2385
    0.4327
    0.9104

T2 = 2×2

    0.8728    0.4880
    0.4880   -0.8728

stats2 = struct with fields:
    loglike: -0.0531
        dfe: 4
      chisq: 5.0335
          p: 0.2839

結果は生のデータを使用した場合と同じになりますが、factoran 以外は共分散データの因子スコア行列 F を計算することができません。

因子負荷量の推定とプロット

標本データを読み込みます。

load carbig

可変行列を定義し、欠損値を含む観測値を削除します。

X = [Acceleration Displacement Horsepower MPG Weight]; 
X = X(all(~isnan(X),2),:);

2 つの共通因子による因子分析で、最小平均二乗誤差予測を使用して、因子負荷量を推定します。リッジ回帰モデルを使用して因子スコアを予測するように指定します。

[Lambda,Psi,T,~,F] = factoran(X,2,Scores="regression")

Lambda = 5×2

   -0.2432   -0.8500
    0.8773    0.3871
    0.7618    0.5930
   -0.7978   -0.2786
    0.9692    0.2129

Psi = 5×1

    0.2184
    0.0804
    0.0680
    0.2859
    0.0152

T = 2×2

    0.9476    0.3195
    0.3195   -0.9476

F = 392×2

    0.4568    0.9158
    0.5897    1.6438
    0.2573    1.6383
    0.3108    1.4154
    0.2700    1.4815
    1.2534    2.0922
    1.1607    2.7986
    1.0866    2.8106
    1.2923    2.6269
    0.5558    2.6860
    0.3443    2.2636
    0.2945    2.3158
    0.6351    1.7573
   -0.3769    4.1067
   -0.8074    0.4072
      ⋮

因子分析モデルでは、$$cov(X)=\Lambda {\Lambda }^T+\Psi$$ であり、$$\Psi$$ の要素が独自因子の分散であると仮定されます。

因子スコア (F) の推定共分散行列を計算します。

inv(T'*T)   % Estimated covariance matrix of F

ans = 2×2

    1.0000    0.0000
    0.0000    1.0000

factoran の既定の回転方法は varimax であるため、T は直交行列で、F の推定共分散行列は単位行列です。

因子分析モデルを使用して X の推定共分散行列を計算します。

Lambda*Lambda' + diag(Psi)   % Estimated covariance matrix of X

ans = 5×5

    1.0000   -0.5424   -0.6893    0.4309   -0.4167
   -0.5424    1.0000    0.8979   -0.8078    0.9328
   -0.6893    0.8979    1.0000   -0.7730    0.8647
    0.4309   -0.8078   -0.7730    1.0000   -0.8326
   -0.4167    0.9328    0.8647   -0.8326    1.0000

$$\Lambda$$ に主軸回転行列を乗算することで、回転していない因子負荷量を計算します。

Lambda*inv(T)   % Unrotate the loadings

ans = 5×2

   -0.5020    0.7277
    0.9550   -0.0865
    0.9113   -0.3185
   -0.8450    0.0091
    0.9865    0.1079

F に T' を乗算することで、回転していない因子スコアを計算します。

F*T'   % Unrotate the factor scores

ans = 392×2

    0.7255   -0.7219
    1.0840   -1.3692
    0.7673   -1.4702
    0.7467   -1.2419
    0.7292   -1.3176
    1.8562   -1.5820
    1.9940   -2.2811
    1.9276   -2.3161
    2.0638   -2.0764
    1.3848   -2.3676
    1.0494   -2.0349
    1.0190   -2.1003
    1.1633   -1.4622
    0.9549   -4.0119
   -0.6349   -0.6438
      ⋮

2 つの因子のバイプロットを作成します。

biplot(Lambda,LineWidth=2,MarkerSize=20)

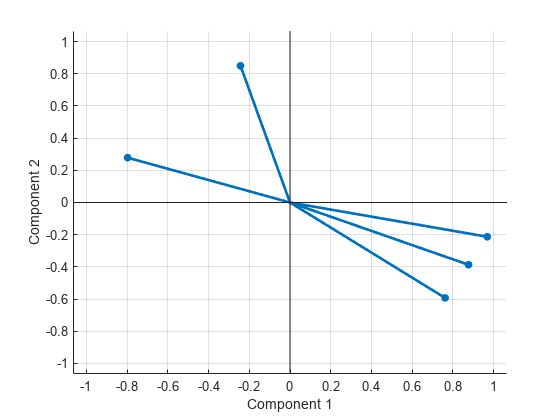
共分散 (または相関) 行列を使用して因子負荷量を推定します。

[Lambda,Psi,T] = factoran(cov(X),2,Xtype="covariance")

Lambda = 5×2

   -0.2432   -0.8500
    0.8773    0.3871
    0.7618    0.5930
   -0.7978   -0.2786
    0.9692    0.2129

Psi = 5×1

    0.2184
    0.0804
    0.0680
    0.2859
    0.0152

T = 2×2

    0.9476    0.3195
    0.3195   -0.9476

cov(X) の代わりに corrcoef(X) を使用して factoran のデータを作成することもできます。

推定値は同じですが、生データではなく共分散行列を使用することで、スコアや有意水準が不要になります。

プロマックス法を使用して因子とスコアを回転します。

[Lambda,Psi,T,stats,F] = factoran(X,2,Rotate="promax");
inv(T'*T)   % Estimated covariance matrix of F, no longer eye(2)

ans = 2×2

    1.0000   -0.6391
   -0.6391    1.0000

Lambda*inv(T'*T)*Lambda'+diag(Psi)   % Estimated covariance matrix of X

ans = 5×5

    1.0000   -0.5424   -0.6893    0.4309   -0.4167
   -0.5424    1.0000    0.8979   -0.8078    0.9328
   -0.6893    0.8979    1.0000   -0.7730    0.8647
    0.4309   -0.8078   -0.7730    1.0000   -0.8326
   -0.4167    0.9328    0.8647   -0.8326    1.0000

斜交軸を重ね合わせて表示し、回転していない変数をプロットします。

invT = inv(T);
Lambda0 = Lambda*invT;
figure()
line([-invT(1,1) invT(1,1) NaN -invT(2,1) invT(2,1)], ...
     [-invT(1,2) invT(1,2) NaN -invT(2,2) invT(2,2)], ...
     Color="b",LineWidth=2)
grid on
hold on
biplot(Lambda0,LineWidth=2,MarkerSize=20)       
xlabel("Loadings for Unrotated Factor 1")
ylabel("Loadings for Unrotated Factor 2")

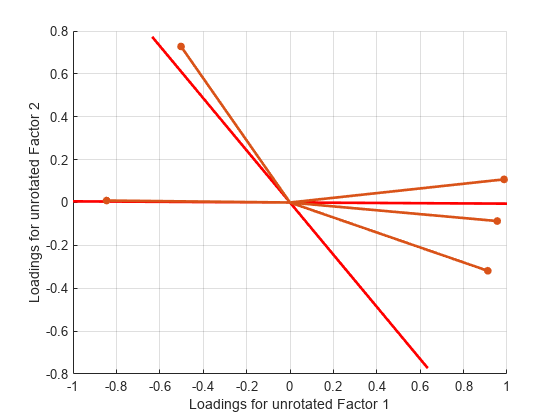
斜交軸に対して回転される変数をプロットします。

figure()
biplot(Lambda,LineWidth=2,MarkerSize=20)

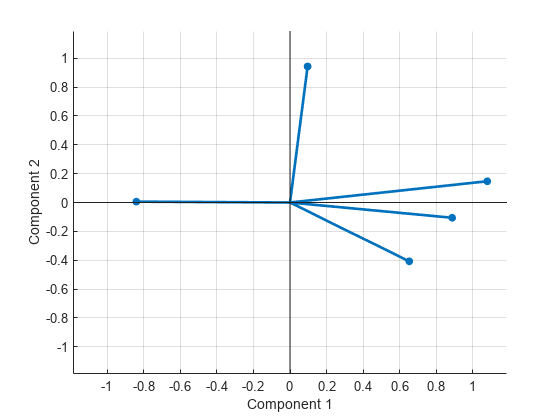
入力引数

X — データ

行列

データ。n 行 d 列の行列として指定します。ここで、各行は d 個の変数で構成される観測値です。

データ型: double

m — 共通因子の数

正の整数

共通因子の数。正の整数として指定します。m の最大許容値は不等式 (d – m)² – d – m ≥ 0 を満たす必要があります。ここで、d は X の変数の数です。この条件により、誤差自由度の値が確実に非負になります (statsを参照)。

例: 3

データ型: double

名前と値の引数

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。

例: lambda = factoran(X,m,'Start',10,'Scores','Thomson') は、10 個の独自因子の分散についての開始点と、因子スコアを予測するトムソン法を使用することを指定します。

Xtype — 入力データ型

'data' (既定値) | 'covariance'

X の入力データ型。'Xtype' と次のいずれかで構成される、コンマ区切りのペアとして指定します。

• 'data' — X は生データです。

• 'covariance' — X は正定値共分散または相関行列です。

例: 'Xtype','covariance'

データ型: char | string

Scores — 因子スコアを予測するメソッド

'wls' または等価な 'Bartlett' (既定値) | 'regression' または等価な 'Thomson'

因子スコアを予測するメソッド。'Scores' と次のいずれかで構成される、コンマ区切りのペアとして指定します。

• 'wls' または等価な 'Bartlett' — F を固定として扱う、重み付き最小二乗推定

• 'regression' または等価な 'Thomson' — リッジ回帰と同じである最小平均二乗誤差予測

例: 'Scores','regression'

データ型: char | string

Start — 最大尤度の最適化における独自因子の分散 psi の開始点

'Rsquared' (既定値) | 'random' | 正の整数 | d 行の行列

最大尤度の最適化における独自因子の分散 psi の開始点。'Start' と次のいずれかで構成される、コンマ区切りのペアとして指定します。

• 'Rsquared' — スケール係数と diag(inv(corrcoef(X))) の積として、出発点のベクトルを選択します (既定の設定)。例については、Jöreskog [2] を参照してください。

• 'random' — 区間 [0,1] の d 一様分布値を選択します。

• 正の整数 — 与えられた回数の最尤近似を、それぞれ 'random' と同じ方法で初期化して実行します。factoran は、最大尤度を使用して近似を返します。

• d 行の行列。指定された行列の各列に対して、1 回の最尤近似を実行します。factoran は i 番目の最適化を i 番目の列の値で初期化します。

例: 'Start',5

データ型: double | char | string

Rotate — 因子負荷量およびスコアの回転に使用するメソッド

'varimax' (既定値) | 'none' | 'quartimax' | 'equamax' | 'parsimax' | 'orthomax' | 'promax' | 'procrustes' | 'pattern' | 関数ハンドル

因子負荷量およびスコアの回転に使用するメソッド。'Rotate' と以下の表のいずれかの値で構成される、コンマ区切りのペアとして指定します。表の説明どおりに関数 rotatefactors の名前と値のペアの引数を追加で指定することにより、回転を制御できます。詳細については、rotatefactors を参照してください。

値	説明
'none'	回転を実行しない
'equamax'	'orthomax' 回転の特殊なケース。回転の詳細を制御するには、引数 'normalize'、'reltol'、および 'maxit' を使用します。
'orthomax'	負荷の分散に基づいて基準を最大化する直交回転。回転の詳細を制御するには、引数 'coeff'、'normalize'、'reltol'、および 'maxit' を使用します。
'parsimax'	オーソマックス回転の特別なケース。回転の詳細を制御するには、引数 'normalize'、'reltol'、および 'maxit' を使用します。
'pattern'	指定された行列のパターンに最も適するように、斜交回転 (既定の設定) または直交回転のどちらかを実行します。回転のタイプを選択するには、引数 'type' を使用します。パターン行列を指定するには、引数 'target' を使用します。
'procrustes'	最小二乗の意味で指定されたターゲット行列に最も適するように、斜交回転 (既定の設定) または直交回転のどちらかを実行します。回転のタイプを選択するには、引数 'type' を使用します。ターゲット行列を指定するには、引数 'target' を使用します。
'promax'	オーソマックス解法の関数として factoran により指定されたターゲット行列に対して、斜交プロクラステス回転を実行します。ターゲット行列を作成するための指数を指定するには、引数 'power' を使用します。'promax' は内部的に 'orthomax' を使用するため、'orthomax' に適用する引数も指定できます。
'quartimax'	'orthomax' 回転の特殊なケース。回転の詳細を制御するには、引数 'normalize'、'reltol'、および 'maxit' を使用します。
'varimax'	'orthomax' 回転の特殊なケース (既定の設定)。回転の詳細を制御するには、引数 'normalize'、'reltol'、および 'maxit' を使用します。
関数ハンドル	次の形式の回転関数の関数ハンドル [B,T] = myrotation(A,...) A は回転していない因子負荷量の d 行 m 列の行列、B は回転される負荷量の d 行 m 列の行列、T は対応する m 行 m 列の回転行列です。 この回転関数に追加の引数を渡すには、factoran の引数 'UserArgs' を使用します。ユーザー定義の回転関数を参照してください。

例: [lambda,psi,T] = factoran(X,m,'Rotate','promax','power',5,'maxit',100)

データ型: char | string | function_handle

Delta — 最大尤度の最適化における psi の下限

0.005 (既定値) | 0 ～ 1 のスカラー

最大尤度の最適化における引数 psi の下限。'Delta' と 0 ～ 1 のスカラー値 (0 < Delta < 1) で構成される、コンマ区切りのペアとして指定します。

例: 0.02

データ型: double

OptimOpts — 最大尤度の最適化のオプション

[] (既定値) | statset によって作成される構造体

最大尤度の最適化のオプション。'OptimOpts' と statset によって作成される構造体で構成される、コンマ区切りのペアとして指定します。オプションのリストに「statset('factoran')」を入力できます。以下の表でも説明しています。

フィールド名 (引数 statset)	意味	値 {既定の設定}
'Display'	アルゴリズムで表示される情報量	{'off'} — 情報表示なし 'final' — 最終出力を表示 'iter' — いくつかの関数ではコマンド ウィンドウに反復出力を表示。それ以外では最終出力を表示
MaxFunEvals	可能な目的関数評価の最大回数	正の整数、{400}
MaxIter	許容される最大反復回数	正の整数、{100}
TolFun	目的関数値の終了許容誤差。連続する関数の値が個別に TolFun 未満になるとソルバーが停止します。	正のスカラー、{1e-8}
TolX	パラメーターの終了許容誤差。連続するパラメーターの値が個別に TolX 未満になるとソルバーが停止します。	正のスカラー、{1e-8}

例: statset('Display','iter')

データ型: struct

Nobs — X を推定するのに使用する観測値の数

正の整数

X を推定するのに使用する観測値の数。'Nobs' と正の整数で構成される、コンマ区切りのペアとして指定します。Nobs は、Xtype が 'covariance' の場合にのみ適用されます。'Nobs' を指定することで、stats 出力構造体フィールド chisq と p を取得できるようになります。

例: 50

データ型: double

出力引数

lambda — 因子負荷量

行列

因子負荷量。d 行 m 列の行列として返されます。d はデータ行列 X の列数、m は factoran の 2 番目の入力引数です。

lambda の (i,j) 番目の要素は、j 番目の変数の i 番目の因子の係数、つまり負荷です。既定の設定では、factoran は関数 rotatefactors を呼び出し、推定された因子負荷量を 'varimax' オプションを使用して回転します。回転の詳細については、因子負荷量およびスコアの回転を参照してください。

psi — 独自因子の分散

ベクトル

独自因子の分散。d 行 1 列のベクトルとして返されます。d はデータ行列 X の列数です。psi のエントリは、最尤推定量です。

T — 因子負荷量回転

行列

因子負荷量回転。m 行 m 列の行列として返されます。m は factoran の 2 番目の入力引数です。回転の詳細については、因子負荷量およびスコアの回転を参照してください。

stats — 共通因子に関する情報

構造体

共通因子に関する情報。構造体として返されます。stats には、共通因子の数が m であるという帰無仮説 H₀ に関連する情報が含まれます[3]。

stats には次のフィールドが含まれます。

フィールド	説明
loglike	最大対数尤度値
dfe	誤差自由度 = ((d – m)2 – d – m)/2 (d は X の変数の数)
chisq	帰無仮説に対するカイ二乗統計近似
p	帰無仮説に対する右裾有意水準

factoran は、dfe が正で、psi における独自因子の分散の推定がすべて正である場合を除き、chisq フィールドと p フィールドを計算しません (ヘイウッド ケースを参照)。X が共分散行列であり、chisq フィールドと p フィールドを計算するために factoran を必要とする場合、名前と値のペアの引数 'Nobs' も指定しなければなりません。

F — 因子スコア

行列

因子スコア。共通因子の予測値とも呼ばれ、n 行 m 列の行列として返されます。n はデータ行列 X の列数、m は factoran の 2 番目の入力引数です。

メモ

X が共分散行列 (Xtype = 'covariance') である場合、factoran は F を計算できません。

factoran は、lambda と同じ基準を使って F を回転します。回転の詳細については、因子負荷量およびスコアの回転を参照してください。

詳細

ヘイウッド ケース

psi の要素が Delta パラメーターの値に等しい場合 (すなわち、それらが本質的にゼロである場合)、この当てはめはヘイウッド ケースとして知られ、推定結果の解釈が不確かになります。特に、尤度の極大値が複数あり、それぞれ負荷と独自因子の分散についての推定が異なる場合があります。ヘイウッド ケースは、過適合 (m が過大) を示す場合がありますが、適合不足になる場合もあります。

因子負荷量およびスコアの回転

名前と値のペアの引数 'Rotate' を使用して回転なしを明示的に指定しない限り、factoran は推定された因子負荷量 lambda、および因子スコア F を回転します。出力行列 T は負荷を回転させるために使用されます。つまり、lambda = lambda0*T となります。ここで、lambda0 は負荷の初期 (非回転) MLE です。T は直交回転の直交行列であり、回転なしの場合は単位行列になります。T の逆行列は主軸回転行列として知られます。一方 T 自体は、参照軸回転行列に関連しています。直交回転に対し、この 2 つは同一です。

factoran は、inv(T') によって回転させた因子スコアを計算します。つまり、F = F0 * inv(T') になります。ここで、F0 には回転していない予測が含まれています。F の推定された共分散は inv(T'*T) で、これは、直交あるいは回転なしの場合、単位行列です。因子負荷量とスコアの回転は、最尤推定後、負荷量行列内に、より容易に解釈できる構造体を作成しようとする試みです。

ユーザー定義の回転関数

ユーザー定義の回転関数に追加の引数を渡す構文は、次のとおりです。

[Lambda,Psi,T] = ...
     factoran(X,2,'Rotate',@myrotation,'UserArgs',1,'two');

参照

[1] Harman, Harry Horace. Modern Factor Analysis. 3rd Ed. Chicago: University of Chicago Press, 1976.

[2] Jöreskog, K. G. “Some Contributions to Maximum Likelihood Factor Analysis.” Psychometrika 32, no. 4 (December 1967): 443–82. https://doi.org/10.1007/BF02289658

[3] Krzanowski, W. J. Principles of Multivariate Analysis: A User's Perspective. New York: Oxford University Press, 1988.

[4] Lawley, D. N., and A. E. Maxwell. Factor Analysis as a Statistical Method. 2nd Ed. New York: American Elsevier Publishing Co., 1971.

拡張機能

tall 配列

メモリの許容量を超えるような多数の行を含む配列を計算します。

pcacov と factoran では、tall 配列を直接操作することはできません。代わりに、C = gather(cov(X)) を使用して tall 配列の共分散行列を計算します。このようにすると、インメモリの共分散行列で処理するために、pcacov または factoran を使用できます。または、pca を tall 配列に対して直接使用できます。

詳細は、メモリに収まらないデータの tall 配列を参照してください。

バージョン履歴

R2006a より前に導入

参考

biplot | pca | procrustes | pcacov | rotatefactors | statset

トピック

• 試験の成績に対する因子分析の実行
• 因子分析の使用による株価の分析