多変量正規分布
概要
多変量正規分布は、一変量正規分布を 2 つ以上の変数に一般化したものです。これは、ベクトルの各要素が一変量正規分布に従う、関連する変数によるランダム ベクトルに対する分布です。最も単純なケースでは、変数間に相関がなく、ベクトルの各要素は一変量正規分布に従う独立確率変数です。
処理が容易なので、多変量正規分布はしばしば多変量データのモデルとして使用されます。
Statistics and Machine Learning Toolbox™ には、多変量正規分布に関連する機能がいくつか用意されています。
パラメーター
多変量正規分布では、次の表のパラメーターを使用します。
| パラメーター | 説明 | 一変量正規分布の類似物 |
|---|---|---|
| μ | 平均ベクトル | 平均値 μ (スカラー) |
| Σ | 共分散行列 - 対角要素には各変数の分散が、非対角要素には変数間の共分散が格納されます | 分散 σ2 (スカラー) |
1 次元の場合は、Σ が標準偏差ではなく分散であることに注意してください。一変量正規分布のパラメーターの詳細については、パラメーターを参照してください。
確率密度関数
d 次元多変量正規分布の確率密度関数 (pdf) は、次のようになります。
ここで、x と μ は 1 行 d 列のベクトル、Σ は d 行 d 列の対称な正定値行列です。
Statistics and Machine Learning Toolbox に関して、以下の点に注意してください。
特異な Σ は、ランダム ベクトルの生成のみについてサポートされます。Σ が特異行列である場合、pdf を同じ形式で記述することはできません。
列ベクトルではなく行ベクトルに基づく x および μ を使用します。
たとえば、二変量正規分布の pdfを参照してください。
累積分布関数
x で評価した多変量正規分布の累積分布関数 (cdf) は、多変量正規分布に従うランダム ベクトル v が (上限が次のように x によって定義される) 半無限の矩形に含まれる確率として定義されます。
多変量正規 cdf に閉形式はありませんが、mvncdf は cdf 値を数値的に計算できます。
たとえば、二変量正規分布の cdfを参照してください。
例
二変量正規分布の pdf
パラメーター mu = [0 0] および Sigma = [0.25 0.3; 0.3 1] をもつ二変量正規分布の pdf を計算し、プロットします。
パラメーター mu および Sigma を定義します。
mu = [0 0]; Sigma = [0.25 0.3; 0.3 1];
2 次元平面内に点が均等間隔で配置されているグリッドを作成します。
x1 = -3:0.2:3; x2 = -3:0.2:3; [X1,X2] = meshgrid(x1,x2); X = [X1(:) X2(:)];
グリッドの点における正規分布の pdf を評価します。
y = mvnpdf(X,mu,Sigma); y = reshape(y,length(x2),length(x1));
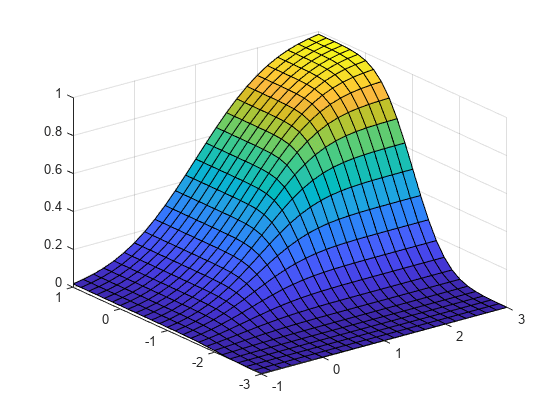
pdf の値をプロットします。
surf(x1,x2,y) axis([-3 3 -3 3 0 0.4]) xlabel('x1') ylabel('x2') zlabel('Probability Density')

二変量正規分布の cdf
二変量正規分布の cdf を計算してプロットします。
平均ベクトル mu と共分散行列 Sigma を定義します。
mu = [1 -1]; Sigma = [.9 .4; .4 .3];
2 次元平面内に 625 個の点が均等間隔で配置されているグリッドを作成します。
[X1,X2] = meshgrid(linspace(-1,3,25)',linspace(-3,1,25)'); X = [X1(:) X2(:)];
グリッドの点における正規分布の cdf を評価します。
p = mvncdf(X,mu,Sigma);
cdf の値をプロットします。
Z = reshape(p,25,25); surf(X1,X2,Z)
矩形領域における確率
二変量正規分布の単位正方形における確率を計算し、結果の等高線図を作成します。
二変量正規分布のパラメーター mu および Sigma を定義します。
mu = [0 0]; Sigma = [0.25 0.3; 0.3 1];
単位正方形における確率を計算します。
p = mvncdf([0 0],[1 1],mu,Sigma)
p = 0.2097
結果を可視化するため、2 次元平面内に点が均等間隔で配置されているグリッドをはじめに作成します。
x1 = -3:.2:3; x2 = -3:.2:3; [X1,X2] = meshgrid(x1,x2); X = [X1(:) X2(:)];
次に、グリッドの点における正規分布の pdf を評価します。
y = mvnpdf(X,mu,Sigma); y = reshape(y,length(x2),length(x1));
そして、単位正方形が含まれている多変量正規分布の等高線図を作成します。
contour(x1,x2,y,[0.0001 0.001 0.01 0.05 0.15 0.25 0.35]) xlabel('x') ylabel('y') line([0 0 1 1 0],[1 0 0 1 1],'Linestyle','--','Color','k')
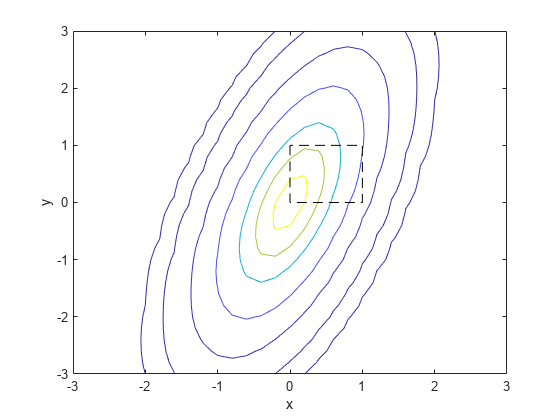
多変量累積確率を計算する場合、一変量確率を計算するよりも非常に多くの計算量を必要とします。既定の設定では、関数 mvncdf はマシンの最大精度に満たない値まで計算し、オプションの 2 番目の出力として誤差の推定値を返します。このケースにおける推定誤差を表示します。
[p,err] = mvncdf([0 0],[1 1],mu,Sigma)
p = 0.2097
err = 1.0000e-08
参照
[1] Kotz, S., N. Balakrishnan, and N. L. Johnson. Continuous Multivariate Distributions: Volume 1: Models and Applications. 2nd ed. New York: John Wiley & Sons, Inc., 2000.
参考
mvncdf | mvnpdf | mvnrnd | NormalDistribution