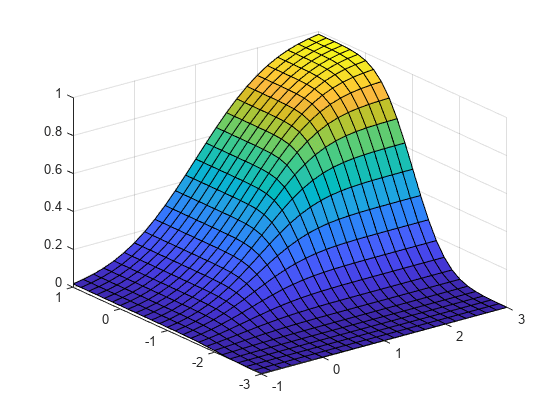
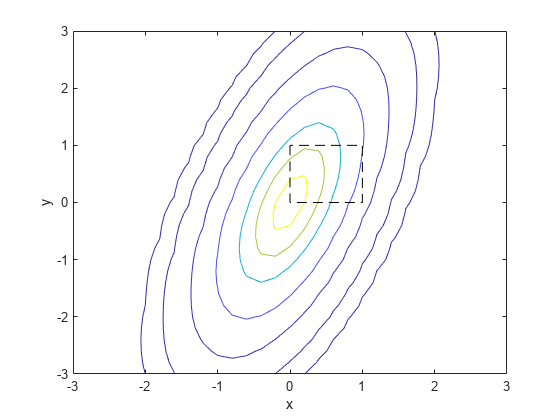
mvncdf
多変量正規累積分布関数
構文
説明
例
入力引数
出力引数
詳細
ヒント
1 次元の場合、
Sigmaは標準偏差ではなく分散です。たとえば、mvncdf(1,0,4)はnormcdf(1,0,2)と同じであり、4は分散、2は標準偏差です。
アルゴリズム
二変量分布と三変量分布の場合、mvncdf は、Drezner および Wesolowsky[1][2]と Genz[3]が開発した手法に基づいて、t 密度の変換に適応求積法を使用します。4 次元以上の場合、mvncdf は、Genz と Bretz[4][5]が開発した手法に基づいて、準モンテカルロ積分アルゴリズムを使用します。
参照
[1] Drezner, Z. “Computation of the Trivariate Normal Integral.” Mathematics of Computation. Vol. 63, 1994, pp. 289–294.
[2] Drezner, Z., and G. O. Wesolowsky. “On the Computation of the Bivariate Normal Integral.” Journal of Statistical Computation and Simulation. Vol. 35, 1989, pp. 101–107.
[3] Genz, A. “Numerical Computation of Rectangular Bivariate and Trivariate Normal and t Probabilities.” Statistics and Computing. Vol. 14, No. 3, 2004, pp. 251–260.
[4] Genz, A., and F. Bretz. “Numerical Computation of Multivariate t Probabilities with Application to Power Calculation of Multiple Contrasts.” Journal of Statistical Computation and Simulation. Vol. 63, 1999, pp. 361–378.
[5] Genz, A., and F. Bretz. “Comparison of Methods for the Computation of Multivariate t Probabilities.” Journal of Computational and Graphical Statistics. Vol. 11, No. 4, 2002, pp. 950–971.
[6] Kotz, S., N. Balakrishnan, and N. L. Johnson. Continuous Multivariate Distributions: Volume 1: Models and Applications. 2nd ed. New York: John Wiley & Sons, Inc., 2000.
拡張機能
バージョン履歴
R2006a で導入