mvnpdf

多変量正規分布の確率密度関数

構文

y = mvnpdf(X)

y = mvnpdf(X,mu)

y = mvnpdf(X,mu,Sigma)

説明

y = mvnpdf(X) は、n 行 d 列の行列 X の各行で評価した、ゼロ平均および単位共分散行列をもつ d 次元多変量正規分布の確率密度関数 (pdf) 値が格納されている n 行 1 列のベクトル y を返します。詳細は、多変量正規分布を参照してください。

y = mvnpdf(X,mu) は、X 内の点の pdf 値を返します。mu によって、関連付けられている各多変量正規分布の平均が決定されます。

y = mvnpdf(X,mu,Sigma) は、X 内の点の pdf 値を返します。Sigma によって、関連付けられている各多変量正規分布の共分散が決定されます。

Sigma のみを指定する場合、mu には既定値のゼロを使用するように [] を指定します。

例

標準多変量正規 pdf

一連のランダムな点で、5 次元標準正規分布の pdf を評価します。

5 次元標準正規分布から 8 つの点を無作為に抽出します。

mu = zeros(1,5);
Sigma = eye(5);
rng('default')  % For reproducibility
X = mvnrnd(mu,Sigma,8)

X = 8×5

    0.5377    3.5784   -0.1241    0.4889   -1.0689
    1.8339    2.7694    1.4897    1.0347   -0.8095
   -2.2588   -1.3499    1.4090    0.7269   -2.9443
    0.8622    3.0349    1.4172   -0.3034    1.4384
    0.3188    0.7254    0.6715    0.2939    0.3252
   -1.3077   -0.0631   -1.2075   -0.7873   -0.7549
   -0.4336    0.7147    0.7172    0.8884    1.3703
    0.3426   -0.2050    1.6302   -1.1471   -1.7115

分布の pdf を X 内の点で評価します。

y = mvnpdf(X)

y = 8×1

    0.0000
    0.0000
    0.0000
    0.0000
    0.0054
    0.0011
    0.0015
    0.0003

pdf 値が最大である X 内の点を求めます。

[maxpdf,idx] = max(y)

maxpdf = 
0.0054

idx = 
5

maxPoint = X(idx,:)

maxPoint = 1×5

    0.3188    0.7254    0.6715    0.2939    0.3252

X 内の 5 番目の点は、無作為に選択した他のどの点よりも pdf 値が大きくなっています。

複数の異なる点で評価した多変量正規 pdf

それぞれ平均が異なる、6 つの 3 次元正規分布を作成します。複数の異なるランダムな点で、各分布の pdf を評価します。

分布の平均 mu と共分散 Sigma を指定します。各分布で共分散行列は同じ (単位行列) です。

firstDim = (1:6)';
mu = repmat(firstDim,1,3)

mu = 6×3

     1     1     1
     2     2     2
     3     3     3
     4     4     4
     5     5     5
     6     6     6

Sigma = eye(3)

Sigma = 3×3

     1     0     0
     0     1     0
     0     0     1

6 つの分布それぞれから無作為に 1 回抽出します。

rng('default')  % For reproducibility
X = mvnrnd(mu,Sigma)

X = 6×3

    1.5377    0.5664    1.7254
    3.8339    2.3426    1.9369
    0.7412    6.5784    3.7147
    4.8622    6.7694    3.7950
    5.3188    3.6501    4.8759
    4.6923    9.0349    7.4897

分布の pdf を X 内の点で評価します。1 番目の分布の pdf は点 X(1,:) で、2 番目の分布の pdf は点 X(2,:) で評価されています。他についても同様です。

y = mvnpdf(X,mu)

y = 6×1

    0.0384
    0.0111
    0.0000
    0.0009
    0.0241
    0.0001

多変量正規 pdf

一連の与えられた点で、2 次元正規分布の pdf を評価します。

分布の平均 mu と共分散 Sigma を指定します。

mu = [1 -1];
Sigma = [0.9 0.4; 0.4 0.3];

分布から無作為に 100 回抽出します。抽出対象の点の行列として X を指定します。

rng('default')  % For reproducibility
X = mvnrnd(mu,Sigma,100);

分布の pdf を X 内の点で評価します。

y = mvnpdf(X,mu,Sigma);

確率密度値をプロットします。

scatter3(X(:,1),X(:,2),y)
xlabel('X1')
ylabel('X2')
zlabel('Probability Density')

同じ点で評価した多変量正規 pdf

10 個の異なる 5 次元正規分布を作成し、指定した点における pdf の値を比較します。

次元 n および d をそれぞれ 10 および 5 に設定します。

n = 10;
d = 5;

多変量正規分布の平均 mu と共分散 Sigma を指定します。すべての分布で同じ平均ベクトルを使用し、共分散行列は変化させます。

mu = ones(1,d)

mu = 1×5

     1     1     1     1     1

mat = eye(d);
nMat = repmat(mat,1,1,n);
var = reshape(1:n,1,1,n);
Sigma = nMat.*var;

Sigma 内の最初の 2 つの共分散行列を表示します。

Sigma(:,:,1:2)

ans = 
ans(:,:,1) =

     1     0     0     0     0
     0     1     0     0     0
     0     0     1     0     0
     0     0     0     1     0
     0     0     0     0     1


ans(:,:,2) =

     2     0     0     0     0
     0     2     0     0     0
     0     0     2     0     0
     0     0     0     2     0
     0     0     0     0     2

5 次元空間におけるランダムな点を x に設定します。

rng('default')  % For reproducibility
x = normrnd(0,1,1,5)

x = 1×5

    0.5377    1.8339   -2.2588    0.8622    0.3188

10 個の分布それぞれについて、x における pdf を評価します。

y = mvnpdf(x,mu,Sigma)

y = 10×1
10-4 ×

    0.2490
    0.8867
    0.8755
    0.7035
    0.5438
    0.4211
    0.3305
    0.2635
    0.2134
    0.1753

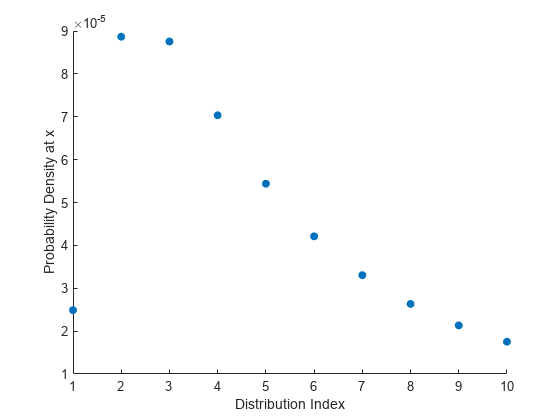
結果をプロットします。

scatter(1:n,y,'filled')
xlabel('Distribution Index')
ylabel('Probability Density at x')

入力引数

X — 評価点

数値ベクトル | 数値行列

評価点。1 行 d 列の数値ベクトルまたは n 行 d 列の数値行列を指定します。n は正の整数スカラー、d は単一の多変量正規分布の次元です。X の行は観測値 (点) に、列は変数 (座標) に対応します。

X がベクトルである場合、mvnpdf は mu の最初の次元または Sigma の最後の次元に一致するようにこのベクトルを複製します。

データ型: single | double

mu — 多変量正規分布の平均

ゼロから成るベクトル (既定値) | 数値ベクトル | 数値行列

多変量正規分布の平均。1 行 d 列の数値ベクトルまたは n 行 d 列の数値行列を指定します。

• mu がベクトルである場合、mvnpdf は Sigma の最後の次元に一致するようにこのベクトルを複製します。

• mu が行列である場合、mu の各行は単一の多変量正規分布の平均ベクトルです。

データ型: single | double

Sigma — 多変量正規分布の共分散

単位行列 (既定値) | 対称な正定値行列 | 数値配列

多変量正規分布の共分散。d 行 d 列の対称な正定値行列または d x d x n の数値配列を指定します。

• Sigma が行列である場合、mvnpdf は mu の行数に一致するようにこの行列を複製します。

• Sigma が配列である場合、Sigma の各ページ Sigma(:,:,i) は単一の多変量正規分布の共分散行列です。したがって、対称な正定値行列になります。

共分散行列が対角行列であり、対角要素に分散が、非対角要素にゼロ共分散が格納されている場合、対角要素のみが格納されている 1 行 d 列のベクトルまたは 1 x d x n の配列を Sigma として指定することもできます。

データ型: single | double

出力引数

y — pdf の値

数値ベクトル

pdf の値。n 行 1 列の数値ベクトルとして返されます。n は、次のいずれかです。

• X が行列である場合、X の行数

• X がベクトルである場合、X を複製した回数

X が行列、mu が行列、Sigma が配列である場合、mvnpdf は X(i,:)、mu(i,:)、Sigma(:,:,i) を使用して y(i) を計算します。

詳細

多変量正規分布

多変量正規分布は、一変量正規分布を 2 つ以上の変数に一般化したものです。平均ベクトル μ および共分散行列 Σ という 2 つのパラメーターがあり、これらは一変量正規分布の平均および分散パラメーターに類似しています。Σ の対角要素には各変数の分散が、Σ の非対角要素には変数間の共分散が格納されます。

d 次元多変量正規分布の確率密度関数 (pdf) は、次のようになります。

$$y\text{ = }f(x,\mu ,\Sigma )\text{ = }\frac{\text{1}}{\sqrt{\left|\Sigma \right|{\text{(2}\pi \text{)}}^d}}\exp \left(-\frac{\text{1}}{\text{2}}\text{(}x\text{-}\mu \text{) }{\Sigma }^{\text{-1}}\text{(}x\text{-}\mu \text{)'}\right)$$

ここで、x と μ は 1 行 d 列のベクトル、Σ は d 行 d 列の対称な正定値行列です。mvnrnd のみが、(特異行列の可能性もある) 半正定値行列の Σ を受け入れます。Σ が特異行列である場合、pdf を同じ形式にすることはできません。

x で評価した多変量正規分布の累積分布関数 (cdf) は、多変量正規分布に従うランダムなベクトル v が、上限が次のように x によって定義される半無限の矩形に含まれる確率です。

$$\mathrm{Pr}\{v(1)\le x(1),v(2)\le x(2),\mathrm{...},v(d)\le x(d)\}.$$

多変量正規 cdf に閉形式はありませんが、mvncdf は cdf 値を数値的に計算できます。

ヒント

• 1 次元の場合、Sigma は標準偏差ではなく分散です。たとえば、mvnpdf(1,0,4) は normpdf(1,0,2) と同じであり、4 は分散、2 は標準偏差です。

参照

[1] Kotz, S., N. Balakrishnan, and N. L. Johnson. Continuous Multivariate Distributions: Volume 1: Models and Applications. 2nd ed. New York: John Wiley & Sons, Inc., 2000.

拡張機能

C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。

GPU 配列

Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

この関数は、GPU 配列を完全にサポートします。詳細は、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2006a より前に導入

参考

mvncdf | mvnrnd | normpdf

トピック

• 多変量正規分布