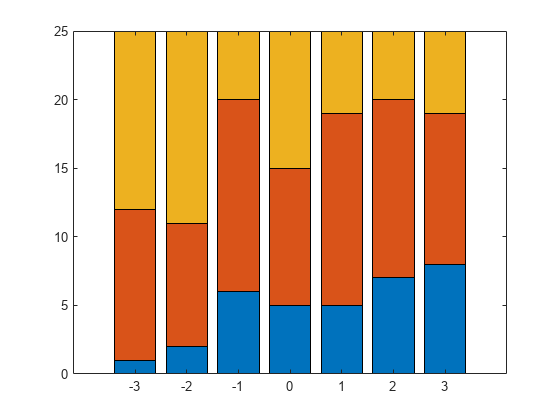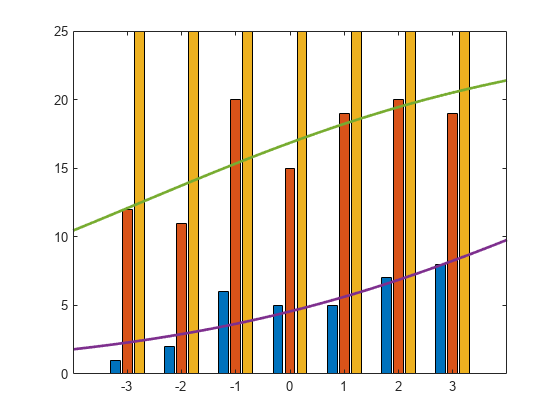mnrval

(非推奨) 多項ロジスティック回帰の値

mnrval は推奨されません。代わりに、fitmnr を使用して MultinomialRegression モデルオブジェクトを作成してから、オブジェクト関数 predict を使用してください。 (R2023a 以降)詳細については、バージョン履歴を参照してください。

構文

pihat = mnrval(B,X)

[pihat,dlow,dhi] = mnrval(B,X,stats)

[pihat,dlow,dhi] = mnrval(B,X,stats,Name,Value)

yhat = mnrval(B,X,ssize)

[yhat,dlow,dhi] = mnrval(B,X,ssize,stats)

[yhat,dlow,dhi] = mnrval(B,X,ssize,stats,Name,Value)

説明

pihat = mnrval(B,X) は、予測子 X と係数推定値 B をもつ多項ロジスティック回帰モデルの予測確率を返します。

pihat は、各多項カテゴリに対する予測確率の n 行 k 列の行列です。B は、mnrfit で返される係数推定を含むベクトルまたは行列です。X は、p 個の予測子の n 個の観測を含む n 行 p 列の行列です。

メモ

mnrval は自動的に定数項をすべてのモデルに含めます。X に 1 の列を入力しないでください。

例

[pihat,dlow,dhi] = mnrval(B,X,stats) は、mnrfit から返される stats 構造体の統計量を使用して、予測確率 pihat の 95% の誤差範囲も返します。

pihat の信頼限界の下限と上限は、それぞれ pihat から dlow を差し引いた値と pihat に dhi を加えた値です。信頼限界は、非同時であり、新規観測ではなく近似曲線にのみ適用します。

例

[pihat,dlow,dhi] = mnrval(B,X,stats,Name,Value) は、1 つ以上の Name,Value ペア引数で指定された追加のオプションを使用して、予測確率と、予測確率 pihat の 95% の誤差範囲を返します。

たとえば、モデルタイプ、リンク関数、返される確率のタイプを指定できます。

yhat = mnrval(B,X,ssize) は、標本サイズ ssize の予測されるカテゴリのカウントを返します。

[yhat,dlow,dhi] = mnrval(B,X,ssize,stats) は、mnrfit から返される stats 構造体の統計量を使用して、予測されるカウント yhat の 95% の誤差範囲も計算します。

yhat の信頼限界の下限と上限は、それぞれ yhat から dlo を差し引いた値と yhat に dhi を加えた値です。信頼限界は、非同時であり、新規観測ではなく近似曲線に適用します。

例

[yhat,dlow,dhi] = mnrval(B,X,ssize,stats,Name,Value) は、1 つ以上の Name,Value ペア引数で指定された追加のオプションを使用して、予測カテゴリカウントと、予測カウント yhat の 95% の誤差範囲を返します。

たとえば、モデルタイプ、リンク関数、返される予測カウントのタイプを指定できます。

例

すべて折りたたむ

ノミナル応答のカテゴリ確率を推定する

ライブスクリプトを開く

ノミナル結果の多項回帰を当てはめて、カテゴリ確率を推定します。

標本データを読み込みます。

load fisheriris

列ベクトル species は、3 種類のアヤメ (setosa、versicolor、virginica) で構成されています。double 行列 meas は、花に関する 4 種類の測定値、がく片の長さと幅 (cm) と花弁の長さと幅 (cm) で構成されています。

ノミナル応答変数を定義します。

sp = nominal(species);
sp = double(sp);

この場合、sp で、1、2、3 はそれぞれ、setosa、versicolor、virginica という種類を表します。

ノミナルモデルを当てはめ、花の測定値を予測子変数として使用して種類を推定します。

[B,dev,stats] = mnrfit(meas,sp);

測定値 (6.3, 2.8, 4.9, 1.7) をもつアヤメの花の特定の種類である確率を推定します。

x = [6.3, 2.8, 4.9, 1.7];
pihat = mnrval(B,x);
pihat

pihat = 1×3

         0    0.3977    0.6023

測定値 (6.3, 2.8, 4.9, 1.7) をもつアヤメの花が setosa である確率は 0、versicolor である確率は 0.3977、virginica である確率は 0.6023 です。

順序応答の確率推定に対する誤差範囲の上限と下限を推定する

ライブスクリプトを開く

カテゴリ間に自然な順序があるカテゴリカル応答について、多項回帰モデルを当てはめます。次に、カテゴリ確率推定に対する信頼限界の上限と下限を推定します。

標本データを読み込み、予測子変数を定義します。

load('carbig.mat')
X = [Acceleration Displacement Horsepower Weight];

予測子変数は、自動車の速度、エンジン排気量、馬力および重量です。応答変数は、ガロンあたりの走行マイル数 (MPG) です。

MPG を 9 ～ 48 mpg の 4 つの水準に分類する順序応答変数を作成します。

miles = ordinal(MPG,{'1','2','3','4'},[],[9,19,29,39,48]);
miles = double(miles);

miles では、1 はガロンあたりの走行マイル数が 9 ～ 19 の自動車を、2 はガロンあたりの走行マイル数が 20 ～ 29 の自動車を示します。同様に、3 と 4 はそれぞれガロンあたりの走行マイル数が 30 ～ 39 と 40 ～ 48 の自動車を示します。

応答変数 miles の多項回帰モデルを当てはめます。順序モデルの場合、既定の 'link' は logit で、既定の 'interactions' は 'off' です。

[B,dev,stats] = mnrfit(X,miles,'model','ordinal');

$x$ = (12、113、110、2670) である自動車のガロンあたりの走行マイル数に対する確率信頼区間の確率推定値と 95% の誤差範囲を計算します。

x = [12,113,110,2670];
[pihat,dlow,hi] = mnrval(B,x,stats,'model','ordinal');
pihat

pihat = 1×4

    0.0615    0.8426    0.0932    0.0027

カテゴリ確率推定に対する信頼限界を計算します。

LL = pihat - dlow;
UL = pihat + hi;
[LL;UL]

ans = 2×4

    0.0073    0.7829    0.0283   -0.0003
    0.1157    0.9022    0.1580    0.0057

ノミナル応答のカテゴリカウントと誤差範囲を推定する

ライブスクリプトを開く

ノミナル結果の多項回帰を当てはめて、カテゴリカウントを推定します。

標本データを読み込みます。

load fisheriris

列ベクトル species は、3 種類のアヤメ setosa、versicolor、virginica で構成されています。double 行列 meas は、花に関する 4 種類の測定値、がく片の長さと幅 (cm) と花弁の長さと幅 (cm) で構成されています。

ノミナル応答変数を定義します。

sp = nominal(species);
sp = double(sp);

この場合、sp で、1、2、3 はそれぞれ、setosa、versicolor、virginica という種類を表します。

ノミナルモデルを当てはめ、花の測定値に基づいて種類を推定します。

[B,dev,stats] = mnrfit(meas,sp);

測定値 (6.3, 2.8, 4.9, 1.7) をもつ 100 本のアヤメの標本について、それぞれの種類のカテゴリ数を推定します。

x = [6.3, 2.8, 4.9, 1.7];
yhat = mnrval(B,x,18)

yhat = 1×3

         0    7.1578   10.8422

カウントの誤差範囲を推定します。

[yhat,dlow,hi] = mnrval(B,x,18,stats,'model','nominal');

カテゴリ確率推定に対する信頼限界を計算します。

LL = yhat - dlow;
UL = yhat + hi;
[LL;UL]

ans = 2×3

         0    3.3019    6.9863
         0   11.0137   14.6981

カウント推定をプロットします。

ライブスクリプトを開く

1 つの予測子変数と、3 つのカテゴリをもつ 1 つのカテゴリカル応答変数を含む標本データを作成します。

x = [-3 -2 -1 0 1 2 3]';
Y = [1 11 13; 2 9 14; 6 14 5; 5 10 10;...
		 5 14 6; 7 13 5; 8 11 6];
[Y x]

ans = 7×4

     1    11    13    -3
     2     9    14    -2
     6    14     5    -1
     5    10    10     0
     5    14     6     1
     7    13     5     2
     8    11     6     3

予測子変数 x の 7 つの異なる値に関する観測があります。応答変数 Y には 3 つのカテゴリがあり、データには、x の観測ごとに、25 の個体のうち、Y の各カテゴリに含まれる数が示されます。たとえば、x が -3 の場合、25 個のうち 1 個がカテゴリ 1、11 個がカテゴリ 2、13 個がカテゴリ 3 として観測されます。同様に、x が 1 の場合、5 個がカテゴリ 1、14 個がカテゴリ 2、6 個がカテゴリ 3 として観測されます。

積み重ね表示棒グラフに、各カテゴリの数と x 値をプロットします。

bar(x,Y,'stacked'); 
ylim([0 25]);

Figure contains an axes object. The axes object contains 3 objects of type bar.

個体の応答カテゴリ確率に対するノミナルモデルを、カテゴリごとに単一の予測子変数 x で個別の傾きを使用して当てはめます。

betaHatNom = mnrfit(x,Y,'model','nominal',...
    'interactions','on')

betaHatNom = 2×2

   -0.6028    0.3832
    0.4068    0.1948

betaHatOrd の最初の行には、最初の 2 つの応答カテゴリの切片項が含まれます。2 番目の行には傾きが含まれます。mnrfit は 3 番目のカテゴリを基準カテゴリとして受け入れるため、3 番目のカテゴリの係数はゼロと見なされます。

3 つの応答カテゴリに対する予測確率を計算します。

xx = linspace(-4,4)';
piHatNom = mnrval(betaHatNom,xx,'model','nominal',...
    'interactions','on');

3 番目のカテゴリになる確率は、単純に 1 - P( $y$ = 1) - P( $y$ = 2) です。

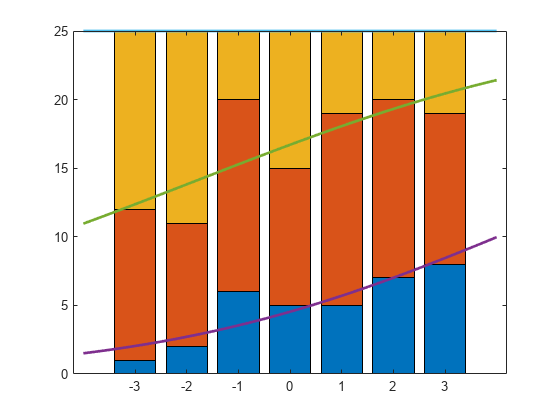
棒グラフに、各カテゴリの推定累積数をプロットします。

line(xx,cumsum(25*piHatNom,2),'LineWidth',2);

Figure contains an axes object. The axes object contains 6 objects of type bar, line.

3 番目のカテゴリに対する累積確率は常に 1 です。

累積応答カテゴリ確率の "平行" 順序のモデルを、すべてのカテゴリで共通する、単一の予測子変数 x の傾きを使用して当てはめます。

betaHatOrd = mnrfit(x,Y,'model','ordinal',...
    'interactions','off')

betaHatOrd = 3×1

   -1.5001
    0.7266
    0.2642

betaHatOrd の最初の 2 つの要素は、最初の 2 つの応答カテゴリの切片項です。betaHatOrd の最後の要素は共通の傾きです。

最初の 2 つの応答カテゴリに対する予測累積確率を計算します。3 番目のカテゴリに対する累積確率は常に 1 です。

piHatOrd = mnrval(betaHatOrd,xx,'type','cumulative',...
    'model','ordinal','interactions','off');

観測された累積数の棒グラフに推定累積数をプロットします。

figure()
bar(x,cumsum(Y,2),'grouped'); 
ylim([0 25]);
line(xx,25*piHatOrd,'LineWidth',2);

Figure contains an axes object. The axes object contains 5 objects of type bar, line.

入力引数

すべて折りたたむ

`B` — 係数推定値
`mnrfit` で返されるベクトルまたは行列

多項ロジスティック回帰モデルの係数推定値。mnrfit によって返されるベクトルまたは行列として指定します。これは、モデルと交互作用に応じてベクトルまたは行列になります。

例: B = mnrfit(X,y); pihat = mnrval(B,X)

データ型: single | double

`X` — 標本データ
行列

予測子の標本データ。n 行 p 列として指定します。X には p 個の予測子に対する n 個の観測が含まれます。

メモ

mnrval は自動的に定数項をすべてのモデルに含めます。X に 1 の列を入力しないでください。

例: pihat = mnrval(B,X)

データ型: single | double

`stats` — モデルの統計量
`mnrfit` によって返される構造体

モデルの統計量。mnrfit によって返される構造体として指定します。カテゴリ確率およびカウントの誤差範囲の上限と下限を計算するには、mnrval で stats 入力引数を使用しなければなりません。

例: [B,dev,stats] = mnrfit(X,y);[pihat,dlo,dhi] = mnrval(B,X,stats)

`ssize` — 標本サイズ
正の整数の列ベクトル

予測子変数の各組み合わせに対して応答カテゴリのアイテムの数を返す標本サイズ。正の整数の n 行 1 列の列ベクトルとして指定します。

たとえば、3 つのカテゴリをもつ応答変数の場合、各カテゴリの個体の数の観測値がそれぞれ y₁、y₂、y₃ である場合、その観測値の標本サイズ m は m = y₁ + y₂ + y₃ になります。

n 個の観測値の標本サイズがベクトル sample に含まれる場合、次のように標本サイズを入力できます。

例: yhat = mnrval(B,X,sample)

データ型: single | double

名前と値の引数

すべて折りたたむ

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。

例: 'model','ordinal','link','probit','type','cumulative' は、プロビットリンク関数をもつ順序モデルの累積確率に対する推定を mnrval が返すことを指定します。

`model` — 多項モデルのタイプ
`'nominal'` (既定値) | `'ordinal'` | `'hierarchical'`

mnrfit で当てはめる多項モデルのタイプ。'model' と、以下のいずれかで構成されるコンマ区切りペアとして指定します。

`'nominal'`	既定の設定。応答カテゴリに順序がない場合に指定します。`model` が `'nominal'` の場合、多項回帰を "ソフトマックス回帰" と呼ぶこともあります。
`'ordinal'`	応答カテゴリに自然な順序がある場合に指定します。
`'hierarchical'`	応答カテゴリの選択が逐次的である場合に指定します。

例: 'model','ordinal'

`interactions` — 多項カテゴリと係数間の交互作用を表すインジケーター
`'on'` | `'off'`

mnrfit で当てはめるモデルの多項カテゴリと係数間の交互作用を表すインジケーター。'interactions' と、以下のいずれかで構成されるコンマ区切りペアとして指定します。

`'on'`	ノミナルモデルと階層モデルの既定値。カテゴリ間で異なる切片と係数をもつモデルを当てはめる場合に指定します。
`'off'`	順序モデルの既定値。すべての多項のカテゴリ間で、切片が異なっていても予測子変数が共通する係数セットをもつモデルを当てはめる場合に指定します。多くの場合、これは "並列回帰" または "比例オッズモデル" と呼ばれます。

例: 'interactions','off'

データ型: logical

`link` — リンク関数
`'logit'` (既定値) | `'probit'` | `'comploglog'` | `'loglog'`

mnrfit が順序モデルと階層モデルに使用するリンク関数。'link' と、以下のいずれかで構成されるコンマ区切りペアとして指定します。

`'logit'`	既定。f(γ) = ln(γ/(1 – γ))
`'probit'`	f(γ) = Φ^-1(γ) — 誤差項は分散 1 で正規分布されます。
`'comploglog'`	相補 log-log f(γ) = ln(–ln(1 –γ))
`'loglog'`	f(γ) = ln(–ln(γ))

リンク関数は、応答確率と、予測子の線形結合である Xβ との関係を定義します。

γ は、モデルが順序応答または逐次的/入れ子応答のどちらに対応するかどうかに応じて、累積確率または条件付き確率の関数になります。

ノミナルモデルの場合は 'link' パラメーターを指定できません。このモデルでは常に多項ロジットリンクを使用します。

$\ln (\frac{π_{j}}{π_{r}}) = β_{j 0} + β_{j 1} X_{j 1} + β_{j 2} X_{j 2} + \dots + β_{j p} X_{j p}, j = 1, \dots, k - 1,$

ここで、π はカテゴリカル確率を表し、r は基準カテゴリに対応します。k は応答カテゴリの総数、p は予測子変数の数です。mnrfit では、ノミナルモデルの基準カテゴリとして最後のカテゴリを使用します。

例: 'link','loglog'

`type` — 推定する確率またはカウントのタイプ
`'category'` (既定値) | `'cumulative'` | `'conditional'`

推定する確率またはカウントのタイプ。'type' と、以下のいずれかを含むコンマ区切りペアとして指定します。

`'category'`	既定の設定。k 個の多項カテゴリの確率 (またはカウント) に対する予測と誤差範囲を返す場合に指定します。
`'cumulative'`	n 行 (k – 1) 列の行列のように、最初の k – 1 個の多項のカテゴリの累積確率 (またはカウント) に対する予測と信頼限界を返すために指定します。k 番目の予測累積確率は常に 1 です。
`'conditional'`	最初の k – 1 の条件付きカテゴリ確率 (カウント) (つまり、結果がカテゴリ j より高いことを前提としたカテゴリ j の確率 (カウント)) について予測および誤差範囲を返す場合に指定します。`'type'` が `'conditional'`で、標本サイズの引数 `ssize` を指定した場合、`X` の各行で予測されるカウントは、すべてのカテゴリで対応する `ssize` の要素を条件とします。

例: 'type','cumulative'

`confidence` — 信頼水準
0.95 (既定値) | (0,1) の範囲のスカラー値

誤差範囲の信頼水準。'confidence' と、(0,1) の範囲内のスカラー値で構成されるコンマ区切りのペアとして指定します。

たとえば、99% の誤差範囲の場合は、次のように信頼度を指定できます。

例: 'confidence',0.99

データ型: single | double

出力引数

すべて折りたたむ

`pihat` — 確率推定
n 行 (k – 1) 列の行列

各多項カテゴリの確率推定。n 行 (k – 1) 列の行列として返されます。ここで、n は観測の数、k は応答カテゴリの数です。

`yhat` — カウント推定
n 行 k – 1 列の行列

各応答カテゴリの数のカウント推定。n 行 k – 1 列の行列として返されます。ここで、n は観測の数、k は応答カテゴリの数です。

`dlow` — 誤差範囲の下限
列ベクトル

pihat または yhat の信頼限界の下限を計算するための誤差範囲の下限。列ベクトルとして返されます。

pihat の信頼限界の下限は、pihat から dlow を差し引いた値です。同様に、yhat の信頼限界の下限は、yhat から dlow を差し引いた値です。信頼限界は、非同時であり、新規観測ではなく近似曲線にのみ適用します。

`dhi` — 誤差範囲の上限
列ベクトル

pihat または yhat の信頼限界の上限を計算するための誤差範囲の上限。列ベクトルとして返されます。

pihat の信頼限界の上限は、pihat に dhi を加算した値です。同様に、yhat の信頼限界の上限は、yhat に dhi を加算した値です。信頼限界は、非同時であり、新規観測ではなく近似曲線にのみ適用します。

参照

[1] McCullagh, P., and J. A. Nelder. Generalized Linear Models. New York: Chapman & Hall, 1990.

バージョン履歴

R2006b で導入

すべて折りたたむ

R2023b: `mnrval` は非推奨

mnrval は推奨されません。代わりに、fitmnr を使用して MultinomialRegression モデルオブジェクトを作成してから、オブジェクト関数 predict を使用して新しいクエリ点でモデルを評価してください。mnrval が削除される予定はありません。

関数 predict が推奨されるのは、MultinomialRegression モデルオブジェクトを入力として受け入れるためです。MultinomialRegression モデルオブジェクトには、オブジェクトの当てはめに使用されたオプションがモデル係数と共に格納されます。一方、mnrval には、モデル係数を mnrfit で係数の当てはめに使用された同じ引数と共に指定しなければなりません。

MultinomialRegression オブジェクトのプロパティの完全な一覧については、MultinomialRegression を参照してください。

参考

mnrval

構文

説明

例

ノミナル応答のカテゴリ確率を推定する

順序応答の確率推定に対する誤差範囲の上限と下限を推定する

ノミナル応答のカテゴリ カウントと誤差範囲を推定する

カウント推定をプロットします。

入力引数

B — 係数推定値 mnrfit で返されるベクトルまたは行列

X — 標本データ 行列

stats — モデルの統計量 mnrfit によって返される構造体

ssize — 標本サイズ 正の整数の列ベクトル

名前と値の引数

model — 多項モデルのタイプ 'nominal' (既定値) | 'ordinal' | 'hierarchical'

interactions — 多項カテゴリと係数間の交互作用を表すインジケーター 'on' | 'off'

link — リンク関数 'logit' (既定値) | 'probit' | 'comploglog' | 'loglog'

type — 推定する確率またはカウントのタイプ 'category' (既定値) | 'cumulative' | 'conditional'

confidence — 信頼水準 0.95 (既定値) | (0,1) の範囲のスカラー値

出力引数

pihat — 確率推定 n 行 (k – 1) 列の行列

yhat — カウント推定 n 行 k – 1 列の行列

dlow — 誤差範囲の下限 列ベクトル

dhi — 誤差範囲の上限 列ベクトル

参照

バージョン履歴

R2023b: mnrval は非推奨

参考

トピック

ノミナル応答のカテゴリカウントと誤差範囲を推定する

`B` — 係数推定値
`mnrfit` で返されるベクトルまたは行列

`X` — 標本データ
行列

`stats` — モデルの統計量
`mnrfit` によって返される構造体

`ssize` — 標本サイズ
正の整数の列ベクトル

`model` — 多項モデルのタイプ
`'nominal'` (既定値) | `'ordinal'` | `'hierarchical'`

`interactions` — 多項カテゴリと係数間の交互作用を表すインジケーター
`'on'` | `'off'`

`link` — リンク関数
`'logit'` (既定値) | `'probit'` | `'comploglog'` | `'loglog'`

`type` — 推定する確率またはカウントのタイプ
`'category'` (既定値) | `'cumulative'` | `'conditional'`

`confidence` — 信頼水準
0.95 (既定値) | (0,1) の範囲のスカラー値

`pihat` — 確率推定
n 行 (k – 1) 列の行列

`yhat` — カウント推定
n 行 k – 1 列の行列

`dlow` — 誤差範囲の下限
列ベクトル

`dhi` — 誤差範囲の上限
列ベクトル

R2023b: `mnrval` は非推奨