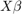glmval

一般化線形モデルの値

構文

yhat = glmval(b,X,link) [yhat,dylo,dyhi] = glmval(b,X,link,stats) [...] = glmval(...,param1,val1,param2,val2,...)

説明

yhat = glmval(b,X,link) は、リンク関数 link と予測子 X を使用した一般化線形モデルに対する予測値を計算します。異なる予測子変数は、X の異なる列に含まれていなければなりません。b は、関数 glmfit で返される係数推定値のベクトルです。link は、関数 glmfit の名前と値のペアの引数 'link' の値として使用されるいずれかの文字ベクトル、string スカラーまたはカスタム定義のリンク関数です。

メモ

既定の設定では、glmval は、モデルの定数項に対応する最初の複数の 1 の列を X に追加します。X に数値 1 だけを続けた列を直接入力しないでください。glmval の既定の動作は、'constant' パラメーターを使用して変更できます。

[yhat,dylo,dyhi] = glmval(b,X,link,stats) は、推定値の 95% の信頼限界も計算します。関数 glmfit の構造体出力 stats を指定した場合、dylo と dyhi も返されます。dylo と dyhi は、信頼限界の下限 yhat-dylo と上限 yhat+dyhi を定義します。信頼限界は非同時です。新しい観測ではなく、近似曲線に適用されます。

[...] = glmval(...,param1,val1,param2,val2,...) は、予測値を制御するオプションのパラメーターの名前と値のペアを指定します。指定可能なパラメーターを次の表に示します。

パラメーター	値
`'confidence'` — 信頼限界に対する信頼水準	0 ～ 1 の間のスカラー
`'size'` — 二項モデルに対するサイズパラメーター (N)	スカラー、または、X の各行に対して 1 つの値をもつベクトル
`'offset'` — 追加の予測子変数として使用。ただし、1.0 で固定した係数値をもちます。	ベクトル
`'constant'`	`'on'` — モデル内の定数項を含みます。定数項の係数は `b` の最初の要素です。 `'off'` — 定数項を省略します。
`'simultaneous'` — 同時信頼区間の計算 (`true`) または非同時信頼区間の計算 (既定の設定は `false`)	`true` または `false`

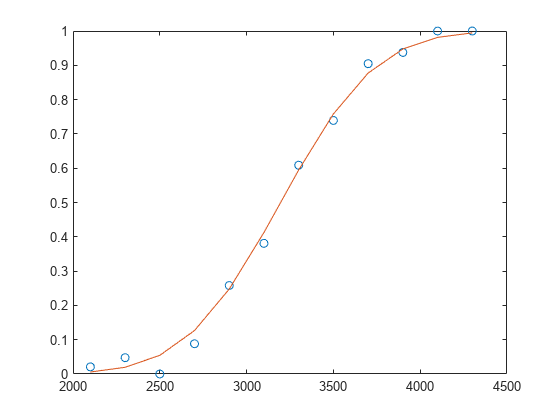
例

すべて折りたたむ

プロビットリンクによる一般化線形モデルの当てはめ

ライブスクリプトを開く

一般化線形回帰モデルを当てはめ、当てはめたモデルを使用して予測子データの予測値 (推定値) を計算します。

標本データセットを作成します。

x = [2100 2300 2500 2700 2900 3100 ...
     3300 3500 3700 3900 4100 4300]';
n = [48 42 31 34 31 21 23 23 21 16 17 21]';
y = [1 2 0 3 8 8 14 17 19 15 17 21]';

x には予測子変数の値が格納されています。y の各値は対応する n の試行回数に対する成功回数です。

x における y についてのプロビット回帰モデルを当てはめます。

b = glmfit(x,[y n],'binomial','Link','probit');

推定成功回数を計算します。

yfit = glmval(b,x,'probit','Size',n);

観測された成功率と推定された成功率を x の値に対してプロットします。

plot(x,y./n,'o',x,yfit./n,'-')

Figure contains an axes object. The axes object contains 2 objects of type line. One or more of the lines displays its values using only markers

カスタム定義のリンク関数の使用

ライブスクリプトを開く

標本データを入力します。

x = [2100 2300 2500 2700 2900 3100 ...
     3300 3500 3700 3900 4100 4300]';
n = [48 42 31 34 31 21 23 23 21 16 17 21]';
y = [1 2 0 3 8 8 14 17 19 15 17 21]';

y の各値は対応する n の試行回数に対する成功回数であり、x には予測子変数の値が格納されています。

@ を使用して作成される 3 つの関数ハンドルを定義します。これらで、プロビットリンク関数に対するリンク、リンクの導関数、逆リンクを定義します。これらのハンドルを cell 配列に格納します。

link = @(mu) norminv(mu);
derlink = @(mu) 1 ./ normpdf(norminv(mu));
invlink = @(resp) normcdf(resp);
F = {link, derlink, invlink};

定義したリンク関数を使用して、x に対する y の一般化線形モデルを当てはめます。

b = glmfit(x,[y n],'binomial','link',F);

推定成功回数を計算します。観測された成功率と推定された成功率を x の値に対してプロットします。

yfit = glmval(b,x,F,'size',n);
plot(x, y./n,'o',x,yfit./n,'-','LineWidth',2)

Figure contains an axes object. The axes object contains 2 objects of type line. One or more of the lines displays its values using only markers

新しいデータから応答を予測する関数からのコード生成

この例では次を使用します。

スクリプトを開く

一般化線形モデルに学習をさせ、モデルに基づいて新しい観測値を分類する関数からコードを生成します。この例はカスタム定義のリンク関数の使用の例に基づいています。

標本データを入力します。

x = [2100 2300 2500 2700 2900 3100 ...
     3300 3500 3700 3900 4100 4300]';
n = [48 42 31 34 31 21 23 23 21 16 17 21]';
y = [1 2 0 3 8 8 14 17 19 15 17 21]';

逆正規 PDF が問題に適しているリンク関数であると仮定します。

$X\beta$ の値を受け入れ、対応する標準正規 CDF の逆関数の値を返す、myInvNorm.m という名前の関数を定義します。

function in = myInvNorm(mu) %#codegen
%myInvNorm Inverse of standard normal cdf for code generation
%   myInvNorm is a GLM link function that accepts a numeric vector mu, and
%   returns in, which is a numeric vector of corresponding values of the
%   inverse of the standard normal cdf.
%   
in = norminv(mu);
end

$X\beta$ の値を受け入れ、対応するリンク関数の導関数の値を返す、myDInvNorm.m という名前の別の関数を定義します。

function din = myDInvNorm(mu) %#codegen
%myDInvNorm Derivative of inverse of standard normal cdf for code
%generation
%   myDInvNorm corresponds to the derivative of the GLM link function
%   myInvNorm. myDInvNorm accepts a numeric vector mu, and returns din,
%   which is a numeric vector of corresponding derivatives of the inverse
%   of the standard normal cdf.
%   
din = 1./normpdf(norminv(mu));
end

$X\beta$ の値を受け入れ、対応するリンク関数の逆関数の値を返す、myInvInvNorm.m という名前の別の関数を定義します。

function iin = myInvInvNorm(mu) %#codegen
%myInvInvNorm Standard normal cdf for code generation
%   myInvInvNorm is the inverse of the GLM link function myInvNorm.
%   myInvInvNorm accepts a numeric vector mu, and returns iin, which is a
%   numeric vector of corresponding values of the standard normal cdf.
% 
iin = normcdf(mu);
end

各リンク関数を指定する構造体配列を作成します。具体的には、'Link'、'Derivative' および 'Inverse' という名前のフィールドを構造体配列に含めます。対応する値は関数の名前です。

link = struct('Link','myInvNorm','Derivative','myDInvNorm',...
    'Inverse','myInvInvNorm')

link = 

  struct with fields:

          Link: 'myInvNorm'
    Derivative: 'myDInvNorm'
       Inverse: 'myInvInvNorm'

リンク関数 link を使用して、x に対する y の GLM を当てはめます。統計量の構造体配列を取得します。

[b,~,stats] = glmfit(x,[y n],'binomial','link',link);

b は、2 行 1 列の回帰係数のベクトルです。

現在の作業フォルダーで、以下を行う classifyGLM.m という名前の関数を定義します。

x の列に対応する列がある測定値、次元が b に対応する回帰係数、リンク関数、GLM 統計量の構造体、および有効な名前と値のペアの引数 glmval を受け入れる
予測と信頼区間の誤差範囲を返す

function [yhat,lo,hi] = classifyGLM(b,x,link,varargin) %#codegen
%CLASSIFYGLM Classify measurements using GLM model 
%   CLASSIFYGLM classifies the n observations in the n-by-1 vector x using
%   the GLM model with regression coefficients b and link function link,
%   and then returns the n-by-1 vector of predicted values in yhat.
%   CLASSIFYGLM also returns margins of error for the predictions using
%   additional information in the GLM statistics structure stats.
narginchk(3,Inf);
if(isstruct(varargin{1}))
    stats = varargin{1};
    [yhat,lo,hi] = glmval(b,x,link,stats,varargin{2:end});
else
    yhat = glmval(b,x,link,varargin{:});
end
end

classifyGLM.m から MEX 関数を生成します。C では静的型付けが使用されるため、codegen は MATLAB® ファイル内のすべての変数のプロパティをコンパイル時に決定しなければなりません。MEX 関数で同じ入力を使用できるようにするため、引数 -args を使用して以下をこの順序で指定します。

回帰係数 b (コンパイル時の定数として)
標本内観測値 x
リンク関数 (コンパイル時の定数として)
生成される GLM 統計量 (コンパイル時の定数として)
名前 'Confidence' (コンパイル時の定数として)
信頼水準 0.9

引数をコンパイル時の定数として指定するため、coder.Constant を使用します。

codegen -config:mex classifyGLM -args {coder.Constant(b),x,coder.Constant(link),coder.Constant(stats),coder.Constant('Confidence'),0.9}

Code generation successful.

codegen は MEX ファイル classifyGLM_mex.mexw64 を現在のフォルダーに生成します。ファイルの拡張子はシステムのプラットフォームによって異なります。

glmval と classifyGLM_mex を使用して、予測を比較します。codegen を呼び出したときの引数 -args と同じ順序で名前と値のペアの引数を指定します。

[yhat1,melo1,mehi1] = glmval(b,x,link,stats,'Confidence',0.9);
[yhat2,melo2,mehi2] = classifyGLM_mex(b,x,link,stats,'Confidence',0.9);

comp1 = (yhat1 - yhat2)'*(yhat1 - yhat2);
agree1 = comp1 < eps
comp2 = (melo1 - melo2)'*(melo1 - melo2);
agree2 = comp2 < eps
comp3 = (mehi1 - mehi2)'*(mehi1 - mehi2);
agree3 = comp3 < eps

agree1 =

  logical

   1


agree2 =

  logical

   1


agree3 =

  logical

   1

生成された MEX 関数は、predict と同じ予測を行います。

参考文献

[1] Dobson, A. J. An Introduction to Generalized Linear Models. New York: Chapman & Hall, 1990.

[2] McCullagh, P., and J. A. Nelder. Generalized Linear Models. New York: Chapman & Hall, 1990.

[3] Collett, D. Modeling Binary Data. New York: Chapman & Hall, 2002.

拡張機能

すべて展開する

C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。

使用上の注意事項および制限事項:

引数	注意と制限
`b`	`b` は、コンパイル時の定数でなければなりません (`codegen` (MATLAB Coder) が C/C++ コードを生成するときに、`b` の値を変更することはできません)。`coder.Constant` (MATLAB Coder) を使用すると、変数をコンパイル時の定数として指定できます。
`X`	倍精度または単精度の数値行列でなければなりません。
`link`	関数ハンドル、つまり `@` を使用して作成された関数をサポートしません。コンパイル時の定数でなければなりません。
`stats`	コンパイル時の定数でなければなりません。
名前と値のペアの引数 `'Constant'`	コンパイル時の定数でなければなりません。
名前と値のペアの引数	名前と値のペアの引数に含まれる名前はコンパイル時の定数でなければなりません。たとえば、0.9 という信頼水準を指定するには、`codegen` の `-args` の値に `{coder.Constant('Confidence'),coder.Constant(0.9)}` を含めます。

コード生成の詳細については、コード生成の紹介および一般的なコード生成のワークフローを参照してください。

GPU 配列
Parallel Computing Toolbox™ を使用してグラフィックス処理装置 (GPU) 上で実行することにより、コードを高速化します。

この関数は、GPU 配列を完全にサポートします。詳細は、GPU での MATLAB 関数の実行 (Parallel Computing Toolbox)を参照してください。

バージョン履歴

R2006a より前に導入

参考

glmfit | GeneralizedLinearModel | fitglm | stepwiseglm

トピック

コード生成の紹介