mnrfit

(非推奨) 多項ロジスティック回帰

ページ内をすべて折りたたむ

mnrfit は推奨されません。代わりに fitmnr を使用してください。 (R2023a 以降)詳細については、バージョン履歴を参照してください。

構文

B = mnrfit(X,Y)

B = mnrfit(X,Y,Name,Value)

[B,dev,stats] = mnrfit(___)

説明

B = mnrfit(X,Y) は、X の予測子における Y のノミナル応答の多項ロジスティック回帰に対する係数推定値の行列 B を返します。

例

B = mnrfit(X,Y,Name,Value) は、1 つ以上の Name,Value ペア引数で指定された追加オプションを使用して、多項モデルの当てはめに対する係数推定値の行列 B を返します。

たとえば、ノミナルモデル、順序モデル、階層モデルを当てはめるか、リンク関数を変更できます。

例

[B,dev,stats] = mnrfit(___) は、当てはめの逸脱度 dev と、前の入力引数のいずれかに対する stats 構造体も返します。stats には、自由度、係数推定値の標準誤差、残差などのモデルの統計量が含まれます。

例

すべて折りたたむ

ノミナル応答の多項回帰

ライブスクリプトを開く

ノミナル結果の多項回帰を当てはめ、結果を解釈します。

標本データを読み込みます。

load fisheriris

列ベクトル species は、3 種類のアヤメ setosa、versicolor、virginica で構成されています。double 行列 meas は、花に関する 4 種類の測定値、がく片の長さと幅 (cm) と花弁の長さと幅 (cm) で構成されています。

categorical 配列を使用してノミナル応答変数を定義します。

sp = categorical(species);

多項回帰モデルを当てはめ、測定値を使用して種類を予測します。

[B,dev,stats] = mnrfit(meas,sp);
B

B = 5×2
10³ ×

    2.0184    0.0426
    0.6739    0.0025
   -0.5682    0.0067
   -0.5164   -0.0094
   -2.7609   -0.0183

これは、4 つのすべての予測子において個別の傾き、つまり meas の各カテゴリをもつ、応答カテゴリ相対リスクのノミナルモデルです。B の最初の行には、最初の 2 つの応答カテゴリ (setosa および versicolor と基準カテゴリ virginica) の相対リスクの切片項が含まれます。最後の 4 つの行には、最初の 2 つのカテゴリのモデルに対する傾きが含まれます。mnrfit は 3 番目のカテゴリを基準カテゴリとして受け入れます。

アヤメの花が種類 2 (versicolor) である場合と種類 3 (virginica) である場合の相対リスクは、2 つの確率 (種類 2 である確率と種類 3 である確率) の比率です。相対リスクのモデルは次のようになります。

$\ln (\frac{π_{v e r s i c o l o r}}{π_{v i r g i n i c a}}) = 42.6 + 2.5 X_{1} + 6.7 X_{2} - 9.4 X_{3} - 18.3 X_{4} .$

係数は、相対リスクに対する予測子変数の影響と、あるカテゴリに含まれる確率と基準カテゴリに含まれる確率の対数オッズの両方を表します。たとえば、他の条件がすべて等しい場合、推定された係数 2.5 は、1 番目の測定値 $X_{1}$ が 1 単位増加すると、種類 3 (virginica) になる場合に対する種類 2 (versicolor) になる場合の相対リスクが exp(2.5) 倍になることを示します。他の条件がすべて等しい場合、 $X_{1}$ が 1 単位増加すると、virginica ではなく versicolor になる相対的な対数オッズは 2.5 倍になります。

係数が無限大または負の無限大に収束する場合、推定される係数はオペレーティングシステムによってわずかに異なる可能性があります。

モデル係数の統計的な有意性を確認します。

stats.p

ans = 5×2

         0    0.0000
         0    0.0281
         0    0.0000
         0    0.0000
         0    0.0000

小さい $p$ 値は、virginica ではなく setosa になる (種類 3 と比較した種類 1 の) 相対的なリスクおよび virginica ではなく versicolor になる (種類 3 と比較した種類 2 の) 相対的なリスクに関してすべての尺度が有意であることを示します。

係数推定値の標準誤差を要求します。

stats.se

ans = 5×2

   12.4038    5.2719
    3.5783    1.1228
    3.1760    1.4789
    3.5403    1.2934
    7.1203    2.0967

係数に対する 95% の信頼限界を計算します。

LL = stats.beta - 1.96.*stats.se;
UL = stats.beta + 1.96.*stats.se;

setosa である場合と virginica である場合の相対リスクのモデルの係数に対する信頼区間 (B の係数の最初の列) を表示します。

[LL(:,1) UL(:,1)]

ans = 5×2
10³ ×

    1.9941    2.0427
    0.6668    0.6809
   -0.5744   -0.5620
   -0.5234   -0.5095
   -2.7749   -2.7470

versicolor である場合と virginica である場合の相対リスクのモデルの係数に対する信頼区間 (B の係数の 2 番目の列) を見つけます。

[LL(:,2) UL(:,2)]

ans = 5×2

   32.3049   52.9707
    0.2645    4.6660
    3.7823    9.5795
  -11.9644   -6.8944
  -22.3957  -14.1766

順序応答の多項回帰

ライブスクリプトを開く

カテゴリ間に自然な順序があるカテゴリカル応答について、多項回帰モデルを当てはめます。

標本データを読み込み、予測子変数を定義します。

load carbig
X = [Acceleration Displacement Horsepower Weight];

予測子変数は、自動車の速度、エンジン排気量、馬力および重量です。応答変数は、ガロンあたりの走行マイル数 (mpg) です。

応答値 9 ～ 19 を 1、20 ～ 29 を 2、30 ～ 39 を 3 および 40 ～ 48 のように 4 の範囲でラベル付けすることで、MPG を 9 から 48 までの 4 つの水準に分類する順序応答変数を作成します。

miles = discretize(MPG,[9,19,29,39,48]);

応答変数 miles の順序応答モデルを当てはめます。

[B,dev,stats] = mnrfit(X,miles,'model','ordinal');
B

B の最初の 3 つの要素はモデルの切片項で、B の最後の 4 つの要素は共変量の係数です。これらはすべてのカテゴリに共通であると仮定します。このモデルは、"並列回帰" ("比例オッズ" モデルとも呼ばれます) に対応します。モデルのカテゴリ間の切片は異なりますが、傾きは共通しています。これは、順序モデルの既定値である 'interactions','off' の名前と値のペア引数を使用して指定できます。

[B(1:3)'; repmat(B(4:end),1,3)]

ans = 5×3

  -16.6895  -11.7208   -8.0606
    0.1048    0.1048    0.1048
    0.0103    0.0103    0.0103
    0.0645    0.0645    0.0645
    0.0017    0.0017    0.0017

モデルのリンク関数は、順序モデルの既定値である logit ('link','logit') です。係数は、自動車の mpg が特定の値以下である場合とその値よりも大きい場合の相対リスクまたは対数オッズを表します。

この例の比例オッズモデルは以下のようになります。

$\begin{array}{l} \ln (\frac{P (m p g \leq 19)}{P (m p g > 19)}) = - 16.6895 + 0.1048 X_{A} + 0.0103 X_{D} + 0.0645 X_{H} + 0.0017 X_{W} \\ \ln (\frac{P (m p g \leq 29)}{P (m p g > 29)}) = - 11.7208 + 0.1048 X_{A} + 0.0103 X_{D} + 0.0645 X_{H} + 0.0017 X_{W} \\ \ln (\frac{P (m p g \leq 39)}{P (m p g > 39)}) = - 8.0606 + 0.1048 X_{A} + 0.0103 X_{D} + 0.0645 X_{H} + 0.0017 X_{W} \end{array}$

たとえば、係数推定値 0.1048 は、他のすべてが一定であるとして、速度での 1 単位の変更が、自動車の mpg が 19 以下である場合と 19 を超える場合、29 以下である場合と 29 を超える場合、39 以下である場合と 39 を超える場合のオッズに exp(0.01048) の係数で影響することを示します。

係数の有意性を評価します。

stats.p

エンジン排気量、馬力および自動車の重量についての $p$ 値 0.035、0.0000 および 0.0118 は、自動車の mpg が特定の値より大きくなるのではなくその値以下になるオッズに関して、これらの因子が有意であることを示しています。

階層型多項回帰モデル

ライブスクリプトを開く

階層型多項回帰モデルを当てはめます。

標本データを読み込みます。

load('smoking.mat');

データセット smoking には、次の 5 つの変数があります。性別、年齢、重量、収縮期血圧、拡張期血圧です。性別はバイナリ変数で、1 は女性患者、0 は男性患者を示します。

応答変数を定義します。

Y = categorical(smoking.Smoker);

Smoker のデータには次の 4 つのカテゴリが含まれています。

0:非喫煙者、1 日に 0 本
1:喫煙者、1 日に 1 ～ 5 本
2:喫煙者、1 日に 6 ～ 10 本
3:喫煙者、1 日に 11 本以上

予測子変数を定義します。

X = [smoking.Sex smoking.Age smoking.Weight...
    smoking.SystolicBP smoking.DiastolicBP];

階層型多項モデルを当てはめます。

[B,dev,stats] = mnrfit(X,Y,'model','hierarchical');
B

B = 6×3

   43.8148    5.9571   44.0712
    1.8709   -0.0230    0.0662
    0.0188    0.0625    0.1335
    0.0046   -0.0072   -0.0130
   -0.2170    0.0416   -0.0324
   -0.2273   -0.1449   -0.4824

B の最初の列には、非喫煙者と喫煙者である場合を比較した相対リスクのモデルについての切片と係数推定値が含まれます。2 番目の列には、対象者を喫煙者として、1 日 1 ～ 5 本吸う場合と、1 日 6 本以上吸う場合の対数オッズをモデル化するパラメーター推定が含まれています。最後の 3 番目の列には、対象者が 1 日 6 本以上吸う喫煙者とすると、1 日 6 ～ 10 本以上吸う場合と、1 日 11 本以上吸う場合の対数オッズをモデル化するパラメーター推定が含まれています。

係数はカテゴリ間で異なります。これは、階層モデルの既定値である 'interactions','on' の名前と値のペア引数を使用して指定できます。したがって、この例のモデルは以下のようになります。

$\ln (\frac{P (y = 0)}{P (y > 0)}) = 43.8148 + 1.8709 X_{S} + 0.0188 X_{A} + 0.0046 X_{W} - 0.2170 X_{S B P} - 0.2273 X_{D B P}$

$\ln (\frac{P (1 \leq y \leq 5)}{P (y > 5)}) = 5.9571 - 0.0230 X_{S} + 0.0625 X_{A} - 0.0072 X_{W} + 0.0416 X_{S B P} - 0.1449 X_{D B P}$

$\ln (\frac{P (6 \leq y \leq 10)}{P (y > 10)}) = 44.0712 + 0.0662 X_{S} + 0.1335 X_{A} - 0.0130 X_{W} - 0.0324 X_{S B P} - 0.4824 X_{D B P}$

たとえば、1.8709 の係数推定値は、他のすべてが一定であることを条件に、喫煙者である場合と非喫煙者である場合の尤度が、性別が女性から男性へ変わると exp(1.8709) = 6.49 倍ずつ増えることを示します。

項の統計的な有意性を評価します。

stats.p

ans = 6×3

    0.0000    0.5363    0.2149
    0.3549    0.9912    0.9835
    0.6850    0.2676    0.2313
    0.9032    0.8523    0.8514
    0.0009    0.5187    0.8165
    0.0004    0.0483    0.0545

性別、年齢、体重は、どの水準においても有意性がありません。0.0009 および 0.0004 という $p$ 値は、喫煙者である場合と非喫煙者である場合の相対リスクにおいて両方のタイプの血圧が有意であることを示しています。0.0483 という $p$ 値は、1 日に 0 ～ 5 本吸う人と 1 日に 5 本より多く吸う人のオッズに対して拡張期血圧のみが有意であることを示しています。同様に、0.0545 という $p$ 値は、1 日に 6 ～ 10 本吸う人と 1 日に 10 本より多く吸う人のオッズに対して拡張期血圧が有意であることを示しています。

有意でない因子が相関するかどうかを確認します。性別でグループ分けされた年齢と体重の散布図を描画します。

figure()
gscatter(smoking.Age,smoking.Weight,smoking.Sex)
legend('Male','Female')
xlabel('Age')
ylabel('Weight')

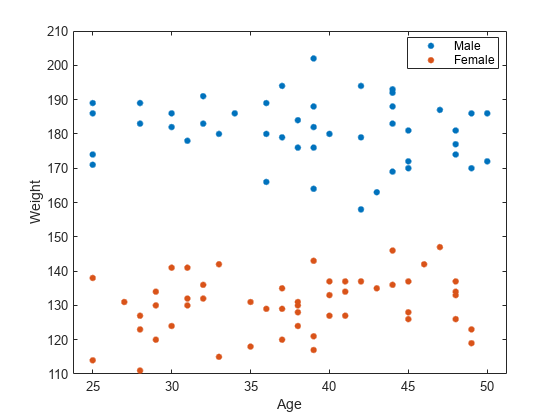
Figure contains an axes object. The axes object with xlabel Age, ylabel Weight contains 2 objects of type line. One or more of the lines displays its values using only markers These objects represent Male, Female.

個人の体重の範囲は、性別によって異なるように見えます。年齢は、性別や体重との明らかな相関はないようです。年齢は有意ではありませんが、体重は性別と相関しているようなので、両方を排除して、モデルを再構築できます。

モデルから年齢と体重を排除し、予測子変数として性別、収縮期血圧、拡張期血圧を使用する階層モデルを当てはめます。

X = double([smoking.Sex smoking.SystolicBP...
smoking.DiastolicBP]);
[B,dev,stats] = mnrfit(X,Y,'model','hierarchical');
B

B = 4×3

   44.8456    5.3230   25.0248
    1.6045    0.2330    0.4982
   -0.2161    0.0497    0.0179
   -0.2222   -0.1358   -0.3092

ここで、1.6045 の係数推定値は、非喫煙者である場合と喫煙者である場合の尤度が、性別が男性から女性へ変わると exp(1.6045) = 4.97 倍増えることを示します。収縮期血圧における単位の増加は、非喫煙者である場合と喫煙者ある場合の尤度が exp(–.2161) = 0.8056 減少することを示します。同様に、拡張期血圧における単位の増加は、非喫煙者である場合と喫煙者ある場合の相対リスクが exp(–.2222) = 0.8007 減少することを示します。

項の統計的な有意性を評価します。

stats.p

ans = 4×3

    0.0000    0.4715    0.2325
    0.0210    0.7488    0.6362
    0.0010    0.4107    0.8899
    0.0003    0.0483    0.0718

0.0210、0.0010、0.0003 という $p$ 値は、モデルの他の項が与えられた場合に、非喫煙者と喫煙者の相対リスクに対して性別および両方のタイプの血圧の項が有意であることを示しています。0.0483 という $p$ 値に基づくと、対象者が喫煙者であることを条件にして、1 日に 1 ～ 5 本吸う場合と 1 日に 5 本より多く吸う場合の相対リスクに対して拡張期血圧は有意であるように見えます。3 番目の列の $p$ 値はどれも 0.05 未満ではないため、この対象者が 1 日に 5 本より多く吸うことを条件にして、6 ～ 10 本吸う場合と 10 本より多く吸う場合の相対リスクに対して、どの変数も統計的に有意ではないことがわかります。

入力引数

すべて折りたたむ

`X` — 予測子変数に関する観測
n 行 p 列の行列

予測子変数に関する観測値。n 行 p 列の行列として指定します。X には p 個の予測子に対する n 個の観測値が含まれます。

メモ

mnrfit は自動的に定数項 (切片) をすべてのモデルに含めます。X に 1 の列を入力しないでください。

データ型: single | double

`Y` — 応答カテゴリラベル
n 行 k 列の行列 | n 行 1 列の数値ベクトル | n 行 1 列の logical ベクトル | n 行 1 列の string ベクトル | n 行 1 列の categorical 配列 | n 行 1 列の文字ベクトルの cell 配列

応答カテゴリラベル。n 行 k 列の行列、または n 行 1 列の数値ベクトル、logical ベクトル、string ベクトル、categorical 配列、文字ベクトルの cell 配列として指定します。

Y が n 行 k 列の行列の場合、n はデータセット内の観測値の数、k は応答カテゴリの数です。Y(i,j) は、X(i,:) で与えられる予測子の組み合わせに対する多項カテゴリ j の結果の数です。この場合、観測値の数は予測子の組み合わせごとの数として判別されます。
Y が n 行 1 列の数値ベクトルの場合、ベクトルは各観測値に対する応答の値を示します。この場合、標本サイズはすべて 1 です。mnrfit は、応答カテゴリを 1 から Y の最大値までの整数値をもつものとして扱います。Y に 1 から Y の最大値までの範囲のすべての整数値が含まれていない場合、mnrfit は、除外された値に対する応答カテゴリを観測値がないものとして扱います。
Y が n 行 1 列の logical ベクトル、string ベクトル、categorical 配列、または文字ベクトルの cell 配列の場合、ベクトルまたは配列は各観測値に対する応答の値を示します。この例ではすべての標本サイズが 1 です。

名前と値の引数

すべて折りたたむ

オプションの引数のペアを Name1=Value1,...,NameN=ValueN として指定します。ここで、Name は引数名で、Value は対応する値です。名前と値の引数は他の引数の後に指定しなければなりませんが、ペアの順序は重要ではありません。

R2021a より前では、名前と値をそれぞれコンマを使って区切り、Name を引用符で囲みます。

例: 'Model','ordinal','Link','probit' は、プロビットリンク関数をもつ順序モデルを指定します。

`Model` — 当てはめるモデルのタイプ
`'nominal'` (既定値) | `'ordinal'` | `'hierarchical'`

当てはめるモデルのタイプ。'Model' と、以下のいずれかで構成されるコンマ区切りペアとして指定します。

`'nominal'`	既定の設定。応答カテゴリに順序はありません。`Model` が `'nominal'` の場合、多項回帰を "ソフトマックス回帰" と呼ぶこともあります。
`'ordinal'`	応答カテゴリは自然な順序になっています。
`'hierarchical'`	応答カテゴリの選択は、逐次的/入れ子です。

例: 'Model','ordinal'

`Interactions` — 多項カテゴリと係数間の交互作用を表すインジケーター
`'on'` | `'off'`

多項カテゴリと係数間の交互作用を表すインジケーター。'Interactions' と、以下のいずれかで構成されるコンマ区切りペアとして指定します。

`'on'`	ノミナルモデルと階層モデルの既定値。カテゴリ間で異なる係数でモデルを当てはめます。
`'off'`	順序モデルの既定値。すべての多項カテゴリ間で予測子変数の係数の共通セットでモデルを当てはめます。多くの場合、これは "並列回帰" または "比例オッズモデル" と呼ばれます。

いずれの場合も、モデルはカテゴリ間で異なる切片をもちます。'Interactions' の選択により、出力配列 B の次元が決まります。

例: 'Interactions','off'

`IterationLimit` — 最大反復回数
100 (既定値) | 正の整数

モデルの当てはめに使用される反復的に再重み付けした最小二乗 (IRLS) の最大反復回数。正の整数として指定します。IterationLimit の既定値は 100 です。

IRLS アルゴリズムの詳細については、反復的に再重み付けした最小二乗を参照してください。

例: IterationLimit=400

データ型: single | double

`Link` — リンク関数
`'logit'` (既定値) | `'probit'` | `'comploglog'` | `'loglog'`

順序モデルと階層モデルに使用するリンク関数。'Link' と、以下のいずれかで構成されるコンマ区切りペアとして指定します。

`'logit'`	既定。f(γ) = ln(γ/(1 –γ))
`'probit'`	f(γ) = Φ^-1(γ) — 誤差項は分散 1 で正規分布されます。
`'comploglog'`	相補 log-log f(γ) = ln(–ln(1 – γ))
`'loglog'`	f(γ) = ln(–ln(γ))

リンク関数は、応答確率と、予測子の線形結合である Xβ との関係を定義します。リンク関数は、モデルが順序応答または逐次的/入れ子応答のどちらに対応するかに応じて、累積確率または条件付き確率の関数になります。たとえば、順序モデルの場合、γ はカテゴリ 1 ～ j になる累積確率と、ロジットリンク関数をもつモデルを次のように表します。

$\ln (\frac{γ}{1 - γ}) = \ln (\frac{π_{1} + π_{2} + \dots + π_{j}}{π_{j + 1} + \dots + π_{k}}) = β_{0 j} + β_{1} X_{1} + β_{2} X_{2} + \dots + β_{p} X_{p},$

ここで、k は最後のカテゴリを表します。

ノミナルモデルの場合は 'Link' パラメーターを指定できません。このモデルでは常に多項ロジットリンクを使用します。

$\ln (\frac{π_{j}}{π_{r}}) = β_{j 0} + β_{j 1} X_{j 1} + β_{j 2} X_{j 2} + \dots + β_{j p} X_{j p}, j = 1, \dots, k - 1,$

ここで、π はカテゴリカル確率を表し、r は基準カテゴリに対応します。mnrfit では、ノミナルモデルの基準カテゴリとして最後のカテゴリを使用します。

例: 'Link','loglog'

`EstDisp` — 分散パラメーターを推定するインジケーター
`'off'` (既定値) | `'on'`

分散パラメーターを推定するインジケーター。'EstDisp' と、以下のいずれかで構成されるコンマ区切りペアとして指定します。

`'off'`	既定の設定。理論分散値 1 を使用します。
`'on'`	標準誤差の計算における多項分布の分散パラメーターを推定します。

例: 'EstDisp','on'

`Tolerance` — 終了許容誤差
`1e-6` (既定値) | 数値スカラー

反復的に再重み付けした最小二乗 (IRLS) 当てはめアルゴリズムの終了許容誤差。数値スカラーとして指定します。mnrfit は、IRLS アルゴリズムの 2 回の反復における各係数の相対差が Tolerance より小さい場合にモデルが収束するものと見なします。Tolerance の既定値は 1e-6 です。

IRLS アルゴリズムの詳細については、反復的に再重み付けした最小二乗を参照してください。

例: Tolerance=1e-4

データ型: single | double

`Weights` — 観測値の重み
n 行 1 列の 1 のベクトル (既定値) | n 行 1 列の数値ベクトル

観測値の重み。n 行 1 列の数値ベクトルとして指定します。ここで、n は観測値の数です。Weights の既定値は n 行 1 列の 1 のベクトルです。

データ型: single | double

出力引数

すべて折りたたむ

`B` — 係数推定値
ベクトル | 行列

Y の応答の多項ロジスティック回帰の係数推定値。ベクトルまたは行列として返されます。

'Interaction' が 'off' の場合、B は k – 1 + p ベクトルになります。B の最初の k – 1 行は、k – 1 多項カテゴリごとに 1 つずつ、切片項に対応し、残りの p 行は最初の k – 1 カテゴリすべてに共通の予測子係数に対応します。
'Interaction' が 'on' の場合、B は (p + 1) 行 (k – 1) 列の行列になります。B の各列は、最初の k – 1 多項カテゴリに 1 つずつ、推定された切片項と予測子係数に対応します。

mnrfit では最後のカテゴリを基準カテゴリとして取るため、k 番目のカテゴリの推定はゼロとして取られます。

`dev` — 当てはめの逸脱度
スカラー値

当てはめの逸脱度。スカラー値として返されます。これは達成可能な最大対数尤度と当てはめたモデルで達成された対数尤度との間の差の 2 倍になります。これは、逸脱度残差の合計に対応します。

$d e v = 2 * \sum_{i}^{n} \sum_{j}^{k} y_{i j} * \log (\frac{y_{i j}}{{\hat{π}}_{i j} * m_{i}}) = \sum_{i}^{n} r d_{i},$

ここで、rd_i は逸脱度残差です。逸脱度残差の詳細は、「stats」を参照してください。

`stats` — モデルの統計量
構造体

モデルの統計量。以下のフィールドを含む構造体として返されます。

`beta`	係数推定値。これらは `B` と同じです。
`dfe`	誤差に対する自由度 `'Interactions'` が `'off'` の場合、自由度は n(k – 1) – (k – 1 + p) です。 `'Interactions'` が `'on'` の場合、自由度は (n – p + 1)(k – 1) です。
`sfit`	推定された分散パラメーター。
`s`	理論的または推定された分散パラメーター。 `'Estdisp'` が `'off'` の場合、`s` は理論的分散パラメーターを表す 1 です。 `'Estdisp'` が `'on'` の場合、`s` は推定された分散パラメーター `sfit` と等しくなります。
`estdisp`	理論的または推定された分散パラメーターのインジケーター。
`se`	係数推定値 `B` の標準誤差。
`coeffcorr`	`B` の推定相関行列。
`covb`	`B` の推定共分散行列。
`t`	`B` の t 統計量。
`p`	`B` の p 値。
`resid`	生の残差。観測値から当てはめ値を減算した値。 $r_{i j} = y_{i j} - {\hat{π}}_{i j} * m_{i}, {\begin{matrix} i = 1, \dots, n \\ j = 1, \dots, k \end{matrix},$ ここで、π_ij はカテゴリカル確率、累積確率または条件付き確率であり、m_i は対応する標本のサイズです。
`residp`	ピアソン残差。これは、推定標準偏差でスケーリングした生の残差です。 $r p_{i j} = \frac{r_{i j}}{{\hat{σ}}_{i j}} = \frac{y_{i j} - {\hat{π}}_{i j} * m_{i}}{\sqrt{{\hat{π}}_{i j} * (1 - {\hat{π}}_{i j}) * m_{i}}}, {\begin{matrix} i = 1, \dots, n \\ j = 1, \dots, k \end{matrix},$ ここで、π_ij はカテゴリカル確率、累積確率または条件付き確率であり、m_i は対応する標本のサイズです。
`residd`	逸脱度残差。 $r d_{i} = 2 * \sum_{j}^{k} y_{i j} * \log (\frac{y_{i j}}{{\hat{π}}_{i j} * m_{i}}), i = 1, \dots, n .$ ここで、π_ij はカテゴリカル確率、累積確率または条件付き確率であり、m_i は対応する標本のサイズです。

アルゴリズム

mnrfit は、X または Y 内の NaN を欠損値として扱い、無視します。

参照

[1] McCullagh, P., and J. A. Nelder. Generalized Linear Models. New York: Chapman & Hall, 1990.

[2] Long, J. S. Regression Models for Categorical and Limited Dependent Variables. Sage Publications, 1997.

[3] Dobson, A. J., and A. G. Barnett. An Introduction to Generalized Linear Models. Chapman and Hall/CRC. Taylor & Francis Group, 2008.

バージョン履歴

R2006b で導入

すべて折りたたむ

R2023b: `mnrfit` は非推奨

mnrfit は推奨されません。代わりに fitmnr を使用してください。mnrfit が削除される予定はありません。

R2023b 以降では、MultinomialRegression モデルオブジェクトの当てはめに関数 fitmnr を使用します。関数 fitmnr には、関数 mnrfit と比べて次のような利点があります。

予測子と応答の入力引数に対する table のサポート
予測子をカテゴリカルとして指定するオプション
観測値の重みを指定するオプション
MultinomialRegression オブジェクトの出力に次のプロパティが含まれます。
- 当てはめた応答値
- 当てはめられたモデルの対数尤度
- モデルの比較基準
- 当てはめたモデルの疑似決定係数の値
MultinomialRegression オブジェクトのプロパティの完全な一覧については、MultinomialRegression を参照してください。

参考

fitmnr | fitglm | mnrval | glmfit | glmval

mnrfit

構文

説明

例

ノミナル応答の多項回帰

順序応答の多項回帰

階層型多項回帰モデル

入力引数

X — 予測子変数に関する観測 n 行 p 列の行列

Y — 応答カテゴリ ラベル n 行 k 列の行列 | n 行 1 列の数値ベクトル | n 行 1 列の logical ベクトル | n 行 1 列の string ベクトル | n 行 1 列の categorical 配列 | n 行 1 列の文字ベクトルの cell 配列

名前と値の引数

Model — 当てはめるモデルのタイプ 'nominal' (既定値) | 'ordinal' | 'hierarchical'

Interactions — 多項カテゴリと係数間の交互作用を表すインジケーター 'on' | 'off'

IterationLimit — 最大反復回数 100 (既定値) | 正の整数

Link — リンク関数 'logit' (既定値) | 'probit' | 'comploglog' | 'loglog'

EstDisp — 分散パラメーターを推定するインジケーター 'off' (既定値) | 'on'

Tolerance — 終了許容誤差 1e-6 (既定値) | 数値スカラー

Weights — 観測値の重み n 行 1 列の 1 のベクトル (既定値) | n 行 1 列の数値ベクトル

出力引数

B — 係数推定値 ベクトル | 行列

dev — 当てはめの逸脱度 スカラー値

stats — モデルの統計量 構造体

アルゴリズム

参照

バージョン履歴

R2023b: mnrfit は非推奨

参考

トピック

`X` — 予測子変数に関する観測
n 行 p 列の行列

`Y` — 応答カテゴリラベル
n 行 k 列の行列 | n 行 1 列の数値ベクトル | n 行 1 列の logical ベクトル | n 行 1 列の string ベクトル | n 行 1 列の categorical 配列 | n 行 1 列の文字ベクトルの cell 配列

`Model` — 当てはめるモデルのタイプ
`'nominal'` (既定値) | `'ordinal'` | `'hierarchical'`

`Interactions` — 多項カテゴリと係数間の交互作用を表すインジケーター
`'on'` | `'off'`

`IterationLimit` — 最大反復回数
100 (既定値) | 正の整数

`Link` — リンク関数
`'logit'` (既定値) | `'probit'` | `'comploglog'` | `'loglog'`

`EstDisp` — 分散パラメーターを推定するインジケーター
`'off'` (既定値) | `'on'`

`Tolerance` — 終了許容誤差
`1e-6` (既定値) | 数値スカラー

`Weights` — 観測値の重み
n 行 1 列の 1 のベクトル (既定値) | n 行 1 列の数値ベクトル

`B` — 係数推定値
ベクトル | 行列

`dev` — 当てはめの逸脱度
スカラー値

`stats` — モデルの統計量
構造体

R2023b: `mnrfit` は非推奨