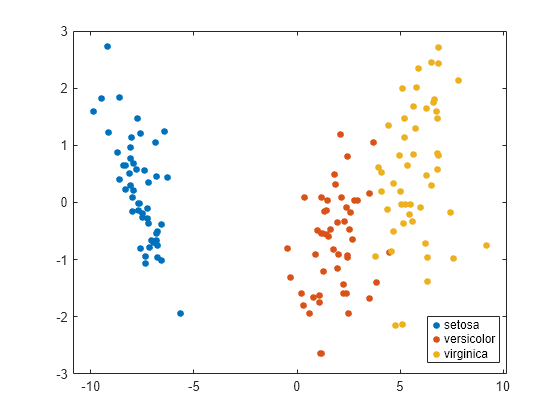
manova1

1 因子多変量分散分析 (MANOVA)

構文

d = manova1(X,group)

d = manova1(X,group,alpha)

[d,p] = manova1(___)

[d,p,stats] = manova1(___)

説明

d = manova1(X,group) は、1 因子多変量分散分析 (MANOVA) を実行し、グループ平均を含んでいる空間の次元の推定 d を返します。MANOVA を実行するために、manova1 は group の因子と X のデータを使用します。

d = manova1(X,group,alpha) は、MANOVA の有意水準も指定します。

[d,p] = manova1(___) は、前の構文におけるいずれかの入力引数の組み合わせを使用して、d に対応する p 値 p も返します。

[d,p,stats] = manova1(___) は、追加の MANOVA 統計量を含む構造体 stats も返します。

例

平均ベクトルを含んでいる空間の次元の計算

carbig データ セットを読み込みます。

load carbig

グループ平均ベクトルを含んでいる空間の次元、および対応する "p" 値を計算します。

[d,p] = manova1([MPG Acceleration Weight Displacement],...
                Origin)

d = 
3

p = 4×1

    0.0000
    0.0000
    0.0075
    0.1934

出力は、平均ベクトルが統計的に同じであるという帰無仮説を棄却するだけの十分な証拠があることを示しています。ただし、平均ベクトルが同じ 3 次元空間にあるという帰無仮説を棄却するだけの十分な証拠はありません。

有意水準の指定と正準変数の検証

fisheriris データ セットを読み込みます。

load fisheriris;

列ベクトル species には、3 種類のアヤメの種 (setosa、versicolor、virginica) が格納されています。行列 meas には、花に関する 4 種類の測定値、がく片の長さと幅 (cm) と花弁の長さと幅 (cm) が格納されています。

1 因子 MANOVA を実行して、4 つの測定値の平均のベクトルが 3 つの花の種のいずれでも同じであるという帰無仮説を検定します。有意水準を指定します。3 種類の花の種のベクトルを含んでいる空間の次元、対応する "p" 値、および MANOVA の追加統計量を計算します。

[d,p,stats] = manova1(meas,species,0.01)

d = 
2

p = 2×1
10-7 ×

    0.0000
    0.5786

stats = struct with fields:
           W: [4×4 double]
           B: [4×4 double]
           T: [4×4 double]
         dfW: 147
         dfB: 2
         dfT: 149
      lambda: [2×1 double]
       chisq: [2×1 double]
     chisqdf: [2×1 double]
    eigenval: [4×1 double]
    eigenvec: [4×4 double]
       canon: [150×4 double]
       mdist: [150×1 double]
      gmdist: [3×3 double]
      gnames: {3×1 cell}

出力は、3 つの種の平均のベクトルが 2 次元空間に格納されていることを示しています。この結果は、ベクトルの 1 つが他とは統計的に異なることを示します。stats 構造体に MANOVA の追加統計量が格納されています。

MANOVA の正準応答データを検証します。

C = stats.canon

C = 150×4

   -8.0618    0.3004    0.0287    0.2769
   -7.1287   -0.7867    0.8907   -0.0714
   -7.4898   -0.2654    0.1792   -0.5257
   -6.8132   -0.6706   -0.3940   -0.7182
   -8.1323    0.5145   -0.4776    0.0508
   -7.7019    1.4617   -0.4069    0.4651
   -7.2126    0.3558   -0.4843   -0.9609
   -7.6053   -0.0116   -0.2433    0.0825
   -6.5606   -1.0152   -0.0342   -1.1131
   -7.3431   -0.9473   -0.0903    0.1119
   -8.3974    0.6474   -0.0926    0.8831
   -7.2193   -0.1096   -1.0216   -0.3382
   -7.3268   -1.0730    0.2403   -0.0866
   -7.5725   -0.8055   -0.0487   -1.1491
   -9.8498    1.5859    0.9619    1.6779
      ⋮

C の各列が正準変数に対応し、各行に X の同じ行に対応する変換されたデータ点が格納されます。正準変数の詳細については、正準変数を参照してください。

1 つ目と 2 つ目の正準変数を使用して散布図を作成します。

gscatter(C(:,1),C(:,2),species)

散布図にデータの主要なクラスターが 2 つ示されます。一方のクラスターに setosa の測定値が含まれ、もう一方に versicolor と virginica の測定値が含まれています。この結果からも、3 つの種の平均のベクトルが 2 次元空間に格納されていることがわかります。

入力引数

X — データ

数値行列

データ。n 行の数値行列として指定します。ここで、n は観測値の数です。X の列は多変量平均の要素に対応します。

データ型: single | double

group — 因子の値

categorical ベクトル | 数値ベクトル | string ベクトル | 文字ベクトルの cell 配列

因子の値。categorical ベクトル、数値ベクトル、string ベクトル、または文字ベクトルの cell 配列として指定します。group には n 個の要素が含まれていなければなりません。ここで、n は X の行数です。group の各要素は、X の対応する行にあるデータの因子の値を表します。

例: [1,2,1,3,1,...,3,1]

例: ["white","red","white",...,"black","red"]

データ型: single | double | string | cell | categorical

alpha — 有意水準

0.05 (既定値) | 0 ～ 1 のスカラー

MANOVA の有意水準。0 ～ 1 のスカラーとして指定します。詳細については、アルゴリズムを参照してください。

例: 0.01

データ型: single | double

出力引数

d — 次元の推定

非負のスカラー

平均ベクトルを含んでいる空間の次元の推定。非負のスカラーとして返されます。d は X の行数以下になります。詳細については、アルゴリズムを参照してください。

p — p 値

非負のベクトル

MANOVA の p 値。長さ d の非負のベクトルとして返されます。p には、manova1 で d を計算するときに検定する各次元の p 値が格納されます。詳細については、アルゴリズムを参照してください。

データ型: single | double

stats — MANOVA の付加的な結果

構造体

MANOVA の付加的な結果。次のフィールドをもつ構造体として返されます。

フィールド	コンテンツ
W	グループ内二乗和およびクロス積行列
B	グループ間二乗和およびクロス積行列
T	二乗総和およびクロス積行列
dfW	W の自由度
dfB	B の自由度
dfT	T の自由度
lambda	ウィルクスのラムダ検定統計量の値のベクトル (平均が 0、1 などの次元をもつかどうかの検定に使用)。
chisq	lambda の近似カイ二乗分布への変換
chisqdf	chisq の自由度
eigenval	W-1B の固有値
eigenvec	W-1B の固有ベクトル (正準変数のグループ内の分散が 1 になるようにスケーリングした正準変数 C に対する係数)
canon	XC*eigenvec (XC は平均を差し引いて列をセンタリングした X) と等しくなる正準変数 (正準変数を参照)。
mdist	各点からそのグループの平均までのマハラノビス距離のベクトル
gmdist	グループ平均の各ペアの間のマハラノビス距離の行列

データ型: struct

詳細

正準変数

正準変数 canon は、グループ間の分離を最大にする元の変数の線形結合です。canon(:,1) は、グループ間の分離が最大になる X の列の線形結合です。あらゆる可能な線形結合の中で、canon(:,1) が 1 因子分散分析 (ANOVA) における最も有意な F 統計をもちます。canon(:,2) は canon(:,1) に直交している状態で分離が最大になります。他についても同様です。

アルゴリズム

manova1 は、d の取り得る値のそれぞれについて検定統計量を計算することで d を求めます。検定統計量の式は次のとおりです。

$$\left(n-1-\frac{l+r}{2}\right)\log (\lambda ),$$

ここで、"n" は観測値の数、"l" は因子の水準の数、"r" は応答変数の数、$$\lambda$$ はウィルクスのラムダです。ウィルクスのラムダの詳細については、反復測定の多変量分散分析を参照してください。

d が取り得る最大の値は、応答変数の数か、因子の水準の数から 1 を引いた値の小さい方になります。d は、"p" が alpha で指定された有意水準を下回る最大の値です。

代替機能

manova1 を使用する代わりに、関数 manova を使用して manova オブジェクトを作成してから、オブジェクト関数 barttest を使用してグループ平均を含んでいる空間の次元を計算できます。関数 manova を使用する利点は次のとおりです。

• 2 因子および N 因子の MANOVA のサポート

• 因子と応答のデータに対する table のサポート

• 当てはめられる MANOVA モデルの係数、誤差の自由度、応答の共分散行列などについての manova オブジェクトの追加プロパティ

参照

[1] Krzanowski, Wojtek. J. Principles of Multivariate Analysis: A User's Perspective. New York: Oxford University Press, 1988.

[2] Morrison, Donald F. Multivariate Statistical Methods. 2nd ed, McGraw-Hill, 1976.

バージョン履歴

R2006a より前に導入

参考

anova1 | canoncorr | gscatter | gplotmatrix | manovacluster

トピック

• グループ化変数