1 標本を取り除いたときの統計

Delete-1 の共分散の変化 (`CovRatio`)

目的

1 標本を取り除いたときの共分散の変化 (CovRatio) により、回帰近似に影響を与える観測値が特定されます。影響力がある観測とは、モデルから除外すると回帰関数が大幅に変化する可能性がある観測を指します。CovRatio の値が 1 + 3*p/n より大きいか 1 – 3*p/n より小さい場合、影響力をもつ点を表しています。ここで、p は回帰係数の数、n は観測値数です。

定義

CovRatio 統計量は、観測値 i が削除された係数共分散行列の行列式と、完全なモデルの共分散行列の行列式の比です。

$CovRatio = \frac{\det {M S E (i) {[X^{'} (i) X (i)]}^{- 1}}}{\det [M S E {(X^{'} X)}^{- 1}]} .$

CovRatio は、当てはめた LinearModel オブジェクトの Diagnostics テーブルにある n 行 1 列のベクトルです。各要素は、対応する要素が削除された状態の推定係数の一般化された分散と、すべてのデータを使用した係数の一般化された分散の比です。

使用方法

近似モデル (mdl など) を取得した後、fitlm または stepwiselm を使用して、次のことを実行できます。

ドット表記でプロパティのインデックスを使用して、CovRatio を表示する。
```
mdl.Diagnostics.CovRatio
```
次の方法で Delete-1 の共分散の変化をプロットする。
```
plotDiagnostics(mdl,'CovRatio')
```
詳細は、LinearModel クラスの plotDiagnostics メソッドを参照してください。

`CovRatio` を使用した、影響を与える観測の特定

ライブスクリプトを開く

この例では、CovRatio 統計を使用してデータの影響力をもつ点を決定する方法を示します。標本データを読み込み、応答変数と予測子変数を定義します。

load hospital
y = hospital.BloodPressure(:,1);
X = double(hospital(:,2:5));

線形回帰モデルをあてはめます。

mdl = fitlm(X,y);

CovRatio 統計量をプロットします。

plotDiagnostics(mdl,'CovRatio')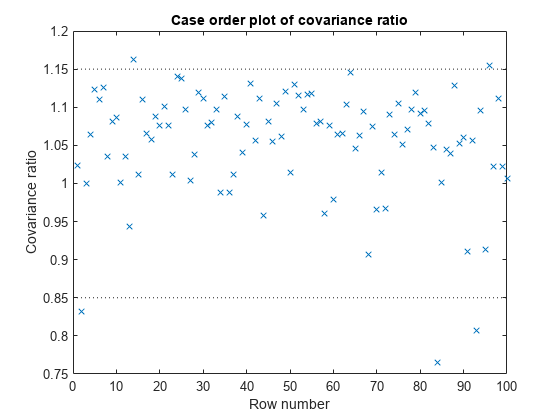

Figure contains an axes object. The axes object with title Case order plot of covariance ratio contains 2 objects of type line. These objects represent Covariance ratio, Reference Line.

この例では、しきい値の限界は 1 + 3*5/100 = 1.15 および 1 – 3*5/100 = 0.85 です。限界範囲の外にあるいくつかの点にも、影響力がある可能性もあります。

限界範囲の外にある観測を特定します。

find((mdl.Diagnostics.CovRatio)>1.15|(mdl.Diagnostics.CovRatio)<0.85)

Delete-1 の係数推定値のスケーリングされた差分 (`Dfbetas`)

目的

係数 j の観測値 i について、Delete-1 の係数推定値のスケーリングされた差分 (Dfbetas) が発生することは、観測値によって回帰係数の推定値が増減するかどうかを示しています。Dfbetas の絶対値は、回帰係数の推定標準偏差に応じた差分の大きさを表します。絶対値が 3/sqrt(n) より大きい Dfbetas 値は、その観測値が対応する係数に与える影響が大きいことを示します。

定義

係数 j と観測値 i の Dfbetas は、すべての観測値を使用した場合の係数 j の推定値と、観測値 i を除外して得られた推定値の差と、観測値 i を除外して得られた係数推定値の標準誤差の比率です。係数 j と観測値 i の Dfbetas は次のようになります。

$D f b e t a s_{i j} = \frac{b_{j} - b_{j (i)}}{\sqrt{M S E_{(i)}} (1 - h_{i i})},$

ここで、b_j は係数 j の推定値、b_j(i) は観測値 i を除外して得られた係数 j の推定値、MSE_(i) は観測値 i を除外して得られた回帰当てはめの平均二乗誤差、h_ii は観測値 i のてこ比値です。Dfbetas は当てはめた LinearModel オブジェクトのテーブル Diagnostics にある n 行 p 列の行列です。Dfbetas の各セルは、対応する観測を削除して得られた、対応する係数の Dfbetas 値です。

使用方法

近似モデル (mdl など) を取得した後、fitlm または stepwiselm によって、ドット表記でプロパティのインデックスを使用して、Dfbetas 値を n 行 p 列の行列として取得できます。

mdl.Diagnostics.Dfbetas

`Dfbetas` を使用した、係数に影響を与える観測値の決定

ライブスクリプトを開く

この例では、Dfbetas を使用して係数に大きな影響を与える観測値を決定する方法を示します。標本データを読み込み、応答変数および独立変数を定義します。

load hospital
y = hospital.BloodPressure(:,1);
X = double(hospital(:,2:5));

線形回帰モデルをあてはめます。

mdl = fitlm(X,y);

絶対値が大きい Dfbetas 値を特定します。

[row,col] = find(abs(mdl.Diagnostics.Dfbetas)>3/sqrt(100));
disp([row col])

Delete-1 の近似値のスケーリングされた変化 (`Dffits`)

目的

Delete-1 の近似値のスケーリングされた変化 (Dffits) は、各観測値が近似応答値に及ぼす影響を表します。絶対値が 2*sqrt(p/n) より大きい Dffits 値は、影響を与える可能性があります。

定義

観測値 i の Dffits は次のようになります。

${Dffits}_{i} = s r_{i} \sqrt{\frac{h_{i i}}{1 - h_{i i}}},$

ここで、sr_i はスチューデント化残差、h_ii は当てはめた LinearModel オブジェクトのてこ比値です。Dffits は当てはめた LinearModel オブジェクトのテーブル Diagnostics にある n 行 1 列のベクトルです。Dffits の各要素は、対応する観測を削除し標準誤差でスケーリングすることにより発生した近似値の変化量です。

使用方法

近似モデル (mdl など) を取得した後、fitlm または stepwiselm を使用して、次のことを実行できます。

ドット表記でプロパティのインデックスを使用して、Dffits 値を表示する。
```
mdl.Diagnostics.Dffits
```
次の方法で、近似値における Delete-1 のスケーリングされた変化をプロットする。
```
plotDiagnostics(mdl,'Dffits')
```
詳細は、LinearModel クラスの plotDiagnostics メソッドを参照してください。

`Dffits` を使用した、近似応答に影響を与える観測値の決定

ライブスクリプトを開く

この例では、Dffits 値を使用して近似された応答値に影響を与える観測値を決定する方法を示します。標本データを読み込み、応答変数および独立変数を定義します。

load hospital
y = hospital.BloodPressure(:,1);
X = double(hospital(:,2:5));

線形回帰モデルをあてはめます。

mdl = fitlm(X,y);

Dffits 値をプロットします。

plotDiagnostics(mdl,'Dffits')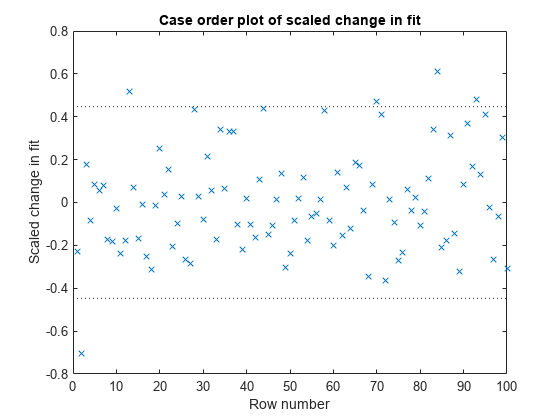

Figure contains an axes object. The axes object with title Case order plot of scaled change in fit contains 2 objects of type line. These objects represent Scaled change in fit, Reference Line.

この例での Dffits の絶対値が影響するしきい値の限界は、2*sqrt(5/100) = 0.45 です。ここでも、Dffits 値を含む観測が推奨限界範囲の外にあることがわかります。

絶対値が大きい Dffits 値を特定します。

find(abs(mdl.Diagnostics.Dffits)>2*sqrt(4/100))

1 標本を取り除いたときの分散 (`S2_i`)

目的

1 標本を取り除いたときの分散 (S2_i) は、ある観測値をデータセットから除外した場合の平均二乗誤差の変化を示します。S2_i の値は、平均二乗誤差の値と比較できます。

定義

S2_i は各観測を順に削除することによって取得した一連の残差分散推定値です。観測値 i の S2_i の値は次のようになります。

$S 2_i = M S E_{(i)} = \frac{\sum_{j \neq i}^{n} {[y_{j} - {\hat{y}}_{j (i)}]}^{2}}{n - p - 1},$

ここで、y_j は j 番目の観測された応答値です。S2_i は、当てはめた LinearModel オブジェクトのテーブル Diagnostics にある n 行 1 列のベクトルです。S2_i の各要素は、当該の観測を削除して得られる回帰の平均二乗誤差です。

使用方法

近似モデル (mdl など) を取得した後、fitlm または stepwiselm を使用して、次のことを実行できます。

ドット表記でプロパティのインデックスを使用して、S2_i ベクトルを表示する。
```
mdl.Diagnostics.S2_i
```
次の方法で、Delete-1 分散値をプロットする。
```
plotDiagnostics(mdl,'S2_i')
```
詳細は、LinearModel クラスの plotDiagnostics メソッドを参照してください。

Delete-1 分散値の計算と調査

ライブスクリプトを開く

この例では、観測値がデータから削除された場合の平均二乗誤差の変化を調べるために、S2_i 値を計算およびプロットする方法を示します。標本データを読み込み、応答変数および独立変数を定義します。

load hospital
y = hospital.BloodPressure(:,1);
X = double(hospital(:,2:5));

線形回帰モデルをあてはめます。

mdl = fitlm(X,y);

モデルの MSE 値を表示します。

mdl.MSE

ans = 23.1140

S2_i 値をプロットします。

plotDiagnostics(mdl,'S2_i')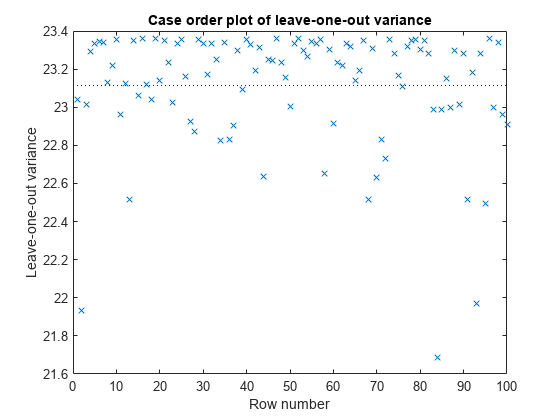

Figure contains an axes object. The axes object with title Case order plot of leave-one-out variance contains 2 objects of type line. These objects represent Leave-one-out variance, Mean squared error.

このプロットにより、S2_i 値を MSE 値 (23.114、横の破線) と簡単に比較できるようになります。1 件の観測値の削除によって、誤差の分散がどのように変化するかを確認できます。

参考

LinearModel | fitlm | stepwiselm | plotDiagnostics | plotResiduals