confusionchart
Create confusion matrix chart for classification problem
Syntax
Description
confusionchart( creates a confusion matrix chart from true labels trueLabels,predictedLabels)trueLabels and predicted labels predictedLabels and returns a ConfusionMatrixChart object. The rows of the confusion matrix correspond to the true class and the columns correspond to the predicted class. Diagonal and off-diagonal cells correspond to correctly and incorrectly classified observations, respectively. Use cm to modify the confusion matrix chart after it is created. For a list of properties, see ConfusionMatrixChart Properties.
confusionchart( creates a confusion matrix chart from the numeric confusion matrix m)m. Use this syntax if you already have a numeric confusion matrix in the workspace.
confusionchart( specifies class labels that appear along the x-axis and y-axis. Use this syntax if you already have a numeric confusion matrix and class labels in the workspace.m,classLabels)
confusionchart( creates the confusion chart in the figure, panel, or tab specified by parent,___)parent.
confusionchart(___, specifies additional Name,Value)ConfusionMatrixChart properties using one or more name-value pair arguments. Specify the properties after all other input arguments. For a list of properties, see ConfusionMatrixChart Properties.
cm = confusionchart(___)ConfusionMatrixChart object. Use cm to modify properties of the chart after creating it. For a list of properties, see ConfusionMatrixChart Properties.
Examples
Create Confusion Matrix Chart
Load Fisher's iris data set.
load fisheriris
X = meas;
Y = species;X is a numeric matrix that contains four petal measurements for 150 irises. Y is a cell array of character vectors that contains the corresponding iris species.
Train a k-nearest neighbor (KNN) classifier, where the number of nearest neighbors in the predictors (k) is 5. A good practice is to standardize numeric predictor data.
Mdl = fitcknn(X,Y,'NumNeighbors',5,'Standardize',1);
Predict the labels of the training data.
predictedY = resubPredict(Mdl);
Create a confusion matrix chart from the true labels Y and the predicted labels predictedY.
cm = confusionchart(Y,predictedY);

The confusion matrix displays the total number of observations in each cell. The rows of the confusion matrix correspond to the true class, and the columns correspond to the predicted class. Diagonal and off-diagonal cells correspond to correctly and incorrectly classified observations, respectively.
By default, confusionchart sorts the classes into their natural order as defined by sort. In this example, the class labels are character vectors, so confusionchart sorts the classes alphabetically. Use sortClasses to sort the classes by a specified order or by the confusion matrix values.
The NormalizedValues property contains the values of the confusion matrix. Display these values using dot notation.
cm.NormalizedValues
ans = 3×3
50 0 0
0 47 3
0 4 46
Modify the appearance and behavior of the confusion matrix chart by changing property values. Add a title.
cm.Title = 'Iris Flower Classification Using KNN';Add column and row summaries.
cm.RowSummary = 'row-normalized'; cm.ColumnSummary = 'column-normalized';

A row-normalized row summary displays the percentages of correctly and incorrectly classified observations for each true class. A column-normalized column summary displays the percentages of correctly and incorrectly classified observations for each predicted class.
Sort Classes by Precision or Recall
Create a confusion matrix chart and sort the classes of the chart according to the class-wise true positive rate (recall) or the class-wise positive predictive value (precision).
Load and inspect the arrhythmia data set.
load arrhythmia
isLabels = unique(Y);
nLabels = numel(isLabels)nLabels = 13
tabulate(categorical(Y))
Value Count Percent
1 245 54.20%
2 44 9.73%
3 15 3.32%
4 15 3.32%
5 13 2.88%
6 25 5.53%
7 3 0.66%
8 2 0.44%
9 9 1.99%
10 50 11.06%
14 4 0.88%
15 5 1.11%
16 22 4.87%
The data contains 16 distinct labels that describe various degrees of arrhythmia, but the response (Y) includes only 13 distinct labels.
Train a classification tree and predict the resubstitution response of the tree.
Mdl = fitctree(X,Y); predictedY = resubPredict(Mdl);
Create a confusion matrix chart from the true labels Y and the predicted labels predictedY. Specify 'RowSummary' as 'row-normalized' to display the true positive rates and false positive rates in the row summary. Also, specify 'ColumnSummary' as 'column-normalized' to display the positive predictive values and false discovery rates in the column summary.
fig = figure; cm = confusionchart(Y,predictedY,'RowSummary','row-normalized','ColumnSummary','column-normalized');
Resize the container of the confusion chart so percentages appear in the row summary.
fig_Position = fig.Position; fig_Position(3) = fig_Position(3)*1.5; fig.Position = fig_Position;
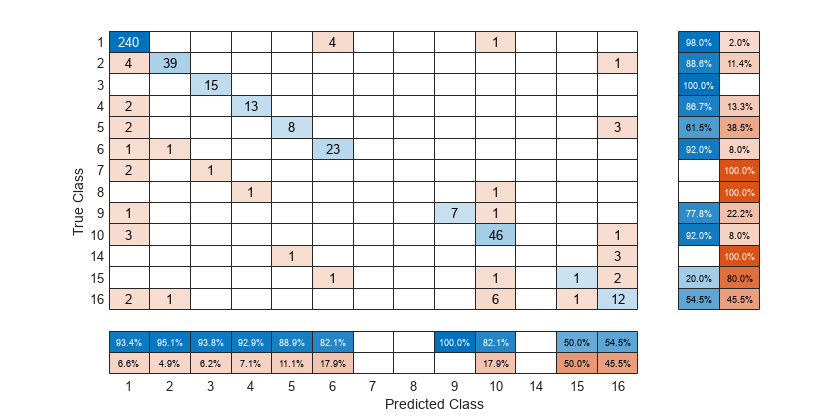
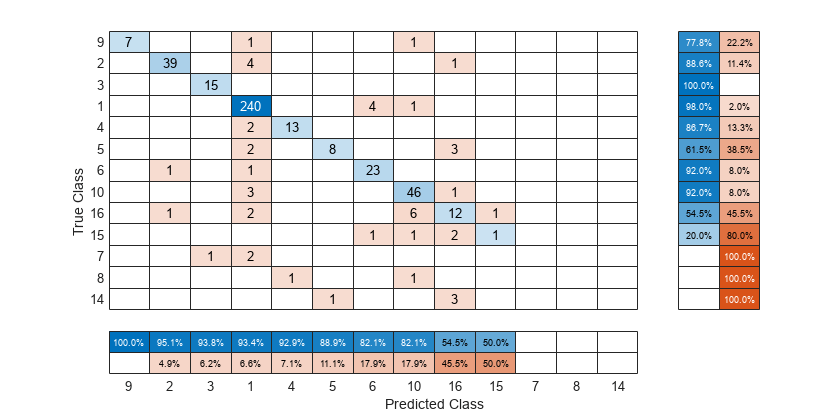
To sort the confusion matrix according to the true positive rate, normalize the cell values across each row by setting the Normalization property to 'row-normalized' and then use sortClasses. After sorting, reset the Normalization property back to 'absolute' to display the total number of observations in each cell.
cm.Normalization = 'row-normalized'; sortClasses(cm,'descending-diagonal') cm.Normalization = 'absolute';
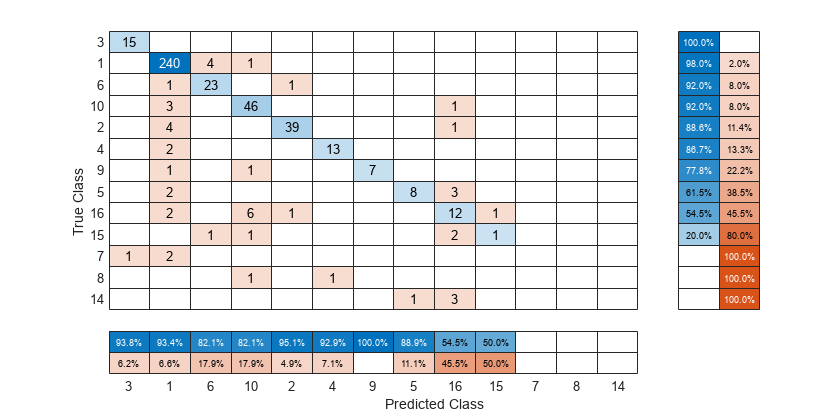
To sort the confusion matrix according to the positive predictive value, normalize the cell values across each column by setting the Normalization property to 'column-normalized' and then use sortClasses. After sorting, reset the Normalization property back to 'absolute' to display the total number of observations in each cell.
cm.Normalization = 'column-normalized'; sortClasses(cm,'descending-diagonal') cm.Normalization = 'absolute';
Confusion Matrix for Classification Using Tall Arrays
Perform classification on a tall array of the Fisher iris data set. Compute a confusion matrix chart for the known and predicted tall labels by using the confusionchart function.
When you perform calculations on tall arrays, MATLAB® uses either a parallel pool (default if you have Parallel Computing Toolbox™) or the local MATLAB session. To run the example using the local MATLAB session when you have Parallel Computing Toolbox, change the global execution environment by using the mapreducer function.
mapreducer(0)
Load Fisher's iris data set.
load fisheririsConvert the in-memory arrays meas and species to tall arrays.
tx = tall(meas); ty = tall(species);
Find the number of observations in the tall array.
numObs = gather(length(ty)); % gather collects tall array into memorySet the seeds of the random number generators using rng and tallrng for reproducibility, and randomly select training samples. The results can vary depending on the number of workers and the execution environment for the tall arrays. For details, see Control Where Your Code Runs.
rng('default') tallrng('default') numTrain = floor(numObs/2); [txTrain,trIdx] = datasample(tx,numTrain,'Replace',false); tyTrain = ty(trIdx);
Fit a decision tree classifier model on the training samples.
mdl = fitctree(txTrain,tyTrain);
Evaluating tall expression using the Local MATLAB Session: - Pass 1 of 2: Completed in 0.51 sec - Pass 2 of 2: Completed in 0.52 sec Evaluation completed in 1.6 sec Evaluating tall expression using the Local MATLAB Session: - Pass 1 of 4: Completed in 0.23 sec - Pass 2 of 4: Completed in 0.31 sec - Pass 3 of 4: Completed in 0.33 sec - Pass 4 of 4: Completed in 0.44 sec Evaluation completed in 1.6 sec Evaluating tall expression using the Local MATLAB Session: - Pass 1 of 4: Completed in 0.088 sec - Pass 2 of 4: Completed in 0.08 sec - Pass 3 of 4: Completed in 0.16 sec - Pass 4 of 4: Completed in 0.17 sec Evaluation completed in 0.72 sec Evaluating tall expression using the Local MATLAB Session: - Pass 1 of 4: Completed in 0.13 sec - Pass 2 of 4: Completed in 0.08 sec - Pass 3 of 4: Completed in 0.21 sec - Pass 4 of 4: Completed in 0.32 sec Evaluation completed in 0.96 sec Evaluating tall expression using the Local MATLAB Session: - Pass 1 of 4: Completed in 0.11 sec - Pass 2 of 4: Completed in 0.12 sec - Pass 3 of 4: Completed in 0.15 sec - Pass 4 of 4: Completed in 0.14 sec Evaluation completed in 0.72 sec
Predict labels for the test samples by using the trained model.
txTest = tx(~trIdx,:); label = predict(mdl,txTest);
Create the confusion matrix chart for the resulting classification.
tyTest = ty(~trIdx); cm = confusionchart(tyTest,label)
Evaluating tall expression using the Local MATLAB Session: - Pass 1 of 1: Completed in 0.049 sec Evaluation completed in 0.18 sec Evaluating tall expression using the Local MATLAB Session: - Pass 1 of 1: Completed in 0.22 sec Evaluation completed in 0.39 sec

cm =
ConfusionMatrixChart with properties:
NormalizedValues: [3x3 double]
ClassLabels: {3x1 cell}
Use GET to show all properties
The confusion matrix chart shows that three measurements in the versicolor class are misclassified. All the measurements belonging to setosa and virginica are classified correctly.
Input Arguments
trueLabels — True labels of classification problem
categorical vector | numeric vector | string vector | character array | cell array of character vectors | logical vector
True labels of classification problem, specified as a categorical vector, numeric vector, string vector, character array, cell array of character vectors, or logical vector. If trueLabels is a vector, then each element corresponds to one observation. If trueLabels is a character array, then it must be two-dimensional with each row corresponding to the label of one observation.
predictedLabels — Predicted labels of classification problem
categorical vector | numeric vector | string vector | character array | cell array of character vectors | logical vector
Predicted labels of classification problem, specified as a categorical vector, numeric vector, string vector, character array, cell array of character vectors, or logical vector. If predictedLabels is a vector, then each element corresponds to one observation. If predictedLabels is a character array, then it must be two-dimensional with each row corresponding to the label of one observation.
m — Confusion matrix
matrix
Confusion matrix, specified as a matrix. m must be square and its elements must be positive integers. The element m(i,j) is the number of times an observation of the ith true class was predicted to be of the jth class. Each colored cell of the confusion matrix chart corresponds to one element of the confusion matrix m.
classLabels — Class labels
categorical vector | numeric vector | string vector | character array | cell array of character vectors | logical vector
Class labels of the confusion matrix chart, specified as a categorical vector, numeric vector, string vector, character array, cell array of character vectors, or logical vector. If classLabels is a vector, then it must have the same number of elements as the confusion matrix has rows and columns. If classLabels is a character array, then it must be two-dimensional with each row corresponding to the label of one class.
parent — Parent container
Figure object | Panel object | Tab object | TiledChartLayout object | GridLayout object
Parent container, specified as a Figure, Panel,
Tab, TiledChartLayout, or GridLayout object.
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Before R2021a, use commas to separate each name and value, and enclose
Name in quotes.
Example: cm = confusionchart(trueLabels,predictedLabels,'Title','My Title
Text','ColumnSummary','column-normalized')
Note
The properties listed here are only a subset. For a complete list, see ConfusionMatrixChart Properties.
Title — Title
'' (default) | character vector | string scalar
Title of the confusion matrix chart, specified as a character vector or string scalar.
Example: cm = confusionchart(__,'Title','My Title
Text')
Example: cm.Title = 'My Title Text'
ColumnSummary — Column summary
'off' (default) | 'absolute' | 'column-normalized' | 'total-normalized'
Column summary of the confusion matrix chart, specified as one of the following:
| Option | Description |
|---|---|
'off' | Do not display a column summary. |
'absolute' | Display the total number of correctly and incorrectly classified observations for each predicted class. |
'column-normalized' | Display the number of correctly and incorrectly classified observations for each predicted class as percentages of the number of observations of the corresponding predicted class. The percentages of correctly classified observations can be thought of as class-wise precisions (or positive predictive values). |
'total-normalized' | Display the number of correctly and incorrectly classified observations for each predicted class as percentages of the total number of observations. |
Example: cm = confusionchart(__,'ColumnSummary','column-normalized')
Example: cm.ColumnSummary = 'column-normalized'
RowSummary — Row summary
'off' (default) | 'absolute' | 'row-normalized' | 'total-normalized'
Row summary of the confusion matrix chart, specified as one of the following:
| Option | Description |
|---|---|
'off' | Do not display a row summary. |
'absolute' | Display the total number of correctly and incorrectly classified observations for each true class. |
'row-normalized' | Display the number of correctly and incorrectly classified observations for each true class as percentages of the number of observations of the corresponding true class. The percentages of correctly classified observations can be thought of as class-wise recalls (or true positive rates). |
'total-normalized' | Display the number of correctly and incorrectly classified observations for each true class as percentages of the total number of observations. |
Example: cm = confusionchart(__,'RowSummary','row-normalized')
Example: cm.RowSummary = 'row-normalized'
Normalization — Normalization of cell values
'absolute' (default) | 'column-normalized' | 'row-normalized' | 'total-normalized'
Normalization of cell values, specified as one of the following:
| Option | Description |
|---|---|
'absolute' | Display the total number of observations in each cell. |
'column-normalized' | Normalize each cell value by the number of observations that has the same predicted class. |
'row-normalized' | Normalize each cell value by the number of observations that has the same true class. |
'total-normalized' | Normalize each cell value by the total number of observations. |
Modifying the normalization of cell values also affects the colors of the cells.
Example: cm = confusionchart(__,'Normalization','total-normalized')
Example: cm.Normalization = 'total-normalized'
Output Arguments
cm — Confusion matrix chart object
ConfusionMatrixChart object
ConfusionMatrixChart object, which is a standalone visualization. Use cm to set properties of the confusion matrix chart after creating it.
Limitations
MATLAB® code generation is not supported for
ConfusionMatrixChartobjects.
More About
Standalone Visualization
A standalone visualization is a chart designed for a special purpose that
works independently from other charts. Unlike other charts such as plot
and surf, a standalone visualization has a preconfigured axes object
built into it, and some customizations are not available. A standalone visualization also
has these characteristics:
It cannot be combined with other graphics elements, such as lines, patches, or surfaces. Thus, the
holdcommand is not supported.The
gcafunction can return the chart object as the current axes.You can pass the chart object to many MATLAB functions that accept an axes object as an input argument. For example, you can pass the chart object to the
titlefunction.
Extended Capabilities
Tall Arrays
Calculate with arrays that have more rows than fit in memory.
This function fully supports tall arrays. For more information, see Tall Arrays.
Version History
Introduced in R2018b
See Also
Functions
Properties
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.

Select a Web Site
Choose a web site to get translated content where available and see local events and offers. Based on your location, we recommend that you select: .
You can also select a web site from the following list:
How to Get Best Site Performance
Select the China site (in Chinese or English) for best site performance. Other MathWorks country sites are not optimized for visits from your location.
Americas
- América Latina (Español)
- Canada (English)
- United States (English)
Europe
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)