oobLoss

Out-of-bag classification loss for bagged classification ensemble model

Syntax

L = oobLoss(ens)

L = oobLoss(ens,Name=Value)

Description

L = oobLoss(ens) returns the classification loss L for the out-of-bag data in the bagged classification ensemble model ens. The interpretation of L depends on the loss function (LossFun). In general, better classifiers yield smaller classification loss values. The default LossFun value is "classiferror" (misclassification rate in decimal).

L = oobLoss(ens,Name=Value) specifies additional options using one or more name-value arguments. For example, you can specify the indices of the weak learners to use for calculating the error, and the aggregation level for the output.

Examples

Estimate Out-Of-Bag Error

Load Fisher's iris data set.

load fisheriris

Grow a bag of 100 classification trees.

ens = fitcensemble(meas,species,'Method','Bag');

Estimate the out-of-bag classification error.

L = oobLoss(ens)

L = 
0.0400

Input Arguments

ens — Bagged classification ensemble model

ClassificationBaggedEnsemble model object

Bagged classification ensemble model, specified as a ClassificationBaggedEnsemble model object trained with fitcensemble.

Name-Value Arguments

Specify optional pairs of arguments as Name1=Value1,...,NameN=ValueN, where Name is the argument name and Value is the corresponding value. Name-value arguments must appear after other arguments, but the order of the pairs does not matter.

Before R2021a, use commas to separate each name and value, and enclose Name in quotes.

Example: oobLoss(ens,Learners=[1 2 3 5],UseParallel=true) specifies to use the first, second, third, and fifth learners in the ensemble, and to perform computations in parallel.

Learners — Indices of weak learners

[1:ens.NumTrained] (default) | vector of positive integers

Indices of the weak learners in the ensemble to use with oobLoss, specified as a vector of positive integers in the range [1:ens.NumTrained]. By default, the function uses all learners.

Example: Learners=[1 2 4]

Data Types: single | double

LossFun — Loss function

"classiferror" (default) | "binodeviance" | "classifcost" | "exponential" | "hinge" | "logit" | "mincost" | "quadratic" | function handle

Loss function, specified as a built-in loss function name or a function handle.

The following table describes the values for the built-in loss functions.

Value	Description
"binodeviance"	Binomial deviance
"classifcost"	Observed misclassification cost
"classiferror"	Misclassified rate in decimal
"exponential"	Exponential loss
"hinge"	Hinge loss
"logit"	Logistic loss
"mincost"	Minimal expected misclassification cost (for classification scores that are posterior probabilities)
"quadratic"	Quadratic loss

• "mincost" is appropriate for classification scores that are posterior probabilities.

• Bagged and subspace ensembles return posterior probabilities by default (ens.Method is "Bag" or "Subspace").

• To use posterior probabilities as classification scores when the ensemble method is "AdaBoostM1", "AdaBoostM2", "GentleBoost", or "LogitBoost", you must specify the double-logit score transform by entering the following:

  ens.ScoreTransform = "doublelogit";

• For all other ensemble methods, the software does not support posterior probabilities as classification scores.

You can specify your own function using function handle notation. Suppose that n is the number of observations in X, and K is the number of distinct classes (numel(ens.ClassNames), where ens is the input model). Your function must have the signature

lossvalue = lossfun(C,S,W,Cost)

where:

• The output argument lossvalue is a scalar.

• You specify the function name (lossfun).

• C is an n-by-K logical matrix with rows indicating the class to which the corresponding observation belongs. The column order corresponds to the class order in ens.ClassNames.

  Create C by setting C(p,q) = 1, if observation p is in class q, for each row. Set all other elements of row p to 0.

• S is an n-by-K numeric matrix of classification scores. The column order corresponds to the class order in ens.ClassNames. S is a matrix of classification scores, similar to the output of predict.

• W is an n-by-1 numeric vector of observation weights. If you pass W, the software normalizes the weights to sum to 1.

• Cost is a K-by-K numeric matrix of misclassification costs. For example, Cost = ones(K) - eye(K) specifies a cost of 0 for correct classification and 1 for misclassification.

For more details on loss functions, see Classification Loss.

Example: LossFun="binodeviance"

Example: LossFun=@Lossfun

Data Types: char | string | function_handle

Mode — Aggregation level for output

"ensemble" (default) | "individual" | "cumulative"

Aggregation level for the output, specified as "ensemble", "individual", or "cumulative".

Value	Description
"ensemble"	The output is a scalar value, the loss for the entire ensemble.
"individual"	The output is a vector with one element per trained learner.
"cumulative"	The output is a vector in which element J is obtained by using learners 1:J from the input list of learners.

Example: Mode="individual"

Data Types: char | string

UseParallel — Flag to run in parallel

false or 0 (default) | true or 1

Flag to run in parallel, specified as a numeric or logical 1 (true) or 0 (false). If you specify UseParallel=true, the oobLoss function executes for-loop iterations by using parfor. The loop runs in parallel when you have Parallel Computing Toolbox™.

Example: UseParallel=true

Data Types: logical

More About

Out of Bag

Bagging, which stands for “bootstrap aggregation,”, is a type of ensemble learning. To bag a weak learner such as a decision tree on a data set, fitcensemble generates many bootstrap replicas of the data set and grows decision trees on these replicas. fitcensemble obtains each bootstrap replica by randomly selecting N observations out of N with replacement, where N is the data set size. To find the predicted response of a trained ensemble, predict take an average over predictions from individual trees.

Drawing N out of N observations with replacement omits on average 37% (1/e) of observations for each decision tree. These are "out-of-bag" observations. For each observation, oobLoss estimates the out-of-bag prediction by averaging over predictions from all trees in the ensemble for which this observation is out of bag. It then compares the computed prediction against the true response for this observation. It calculates the out-of-bag error by comparing the out-of-bag predicted responses against the true responses for all observations used for training. This out-of-bag average is an unbiased estimator of the true ensemble error.

Classification Loss

Classification loss functions measure the predictive inaccuracy of classification models. When you compare the same type of loss among many models, a lower loss indicates a better predictive model.

Consider the following scenario.

• L is the weighted average classification loss.

• n is the sample size.

• For binary classification:

  • y_j is the observed class label. The software codes it as –1 or 1, indicating the negative or positive class (or the first or second class in the ClassNames property), respectively.

  • f(X_j) is the positive-class classification score for observation (row) j of the predictor data X.

  • m_j = y_jf(X_j) is the classification score for classifying observation j into the class corresponding to y_j. Positive values of m_j indicate correct classification and do not contribute much to the average loss. Negative values of m_j indicate incorrect classification and contribute significantly to the average loss.

• For algorithms that support multiclass classification (that is, K ≥ 3):

  • y_j^* is a vector of K – 1 zeros, with 1 in the position corresponding to the true, observed class y_j. For example, if the true class of the second observation is the third class and K = 4, then y₂^* = [0 0 1 0]′. The order of the classes corresponds to the order in the ClassNames property of the input model.

  • f(X_j) is the length K vector of class scores for observation j of the predictor data X. The order of the scores corresponds to the order of the classes in the ClassNames property of the input model.

  • m_j = y_j^*′f(X_j). Therefore, m_j is the scalar classification score that the model predicts for the true, observed class.

• The weight for observation j is w_j. The software normalizes the observation weights so that they sum to the corresponding prior class probability stored in the Prior property. Therefore,

  $${\displaystyle \sum _{j=1}^n{w}_j}=1.$$

Given this scenario, the following table describes the supported loss functions that you can specify by using the LossFun name-value argument.

Loss Function	Value of LossFun	Equation
Binomial deviance	"binodeviance"	$$L={\displaystyle \sum _{j=1}^n{w}_j\log \left\{1+\exp \left[-2m_j\right]\right\}}.$$
Observed misclassification cost	"classifcost"	$$L={\displaystyle \sum _{j=1}^n{w}_j}{c}_{y_j{\widehat{y}}_j},$$ where $${\widehat{y}}_j$$ is the class label corresponding to the class with the maximal score, and $$c_{y_j{\widehat{y}}_j}$$ is the user-specified cost of classifying an observation into class $${\widehat{y}}_j$$ when its true class is yj.
Misclassified rate in decimal	"classiferror"	$$L={\displaystyle \sum _{j=1}^n{w}_j}I\left\{{\widehat{y}}_j\ne y_j\right\},$$ where I{·} is the indicator function.
Cross-entropy loss	"crossentropy"	"crossentropy" is appropriate only for neural network models. The weighted cross-entropy loss is $$L=-{\displaystyle \sum _{j=1}^n\frac{{\tilde{w}}_j\log (m_j)}{Kn}},$$ where the weights $${\tilde{w}}_j$$ are normalized to sum to n instead of 1.
Exponential loss	"exponential"	$$L={\displaystyle \sum _{j=1}^n{w}_j\exp \left(-m_j\right)}.$$
Hinge loss	"hinge"	$$L={\displaystyle \sum }_{j=1}^n{w}_j\max \left\{0,1-m_j\right\}.$$
Logit loss	"logit"	$$L={\displaystyle \sum _{j=1}^n{w}_j\log \left(1+\exp \left(-m_j\right)\right)}.$$
Minimal expected misclassification cost	"mincost"	"mincost" is appropriate only if classification scores are posterior probabilities. The software computes the weighted minimal expected classification cost using this procedure for observations j = 1,...,n. Estimate the expected misclassification cost of classifying the observation Xj into the class k: $${\gamma }_{jk}={\left(f{\left(X_j\right)}^{\prime }C\right)}_k.$$ f(Xj) is the column vector of class posterior probabilities for the observation Xj. C is the cost matrix stored in the Cost property of the model. For observation j, predict the class label corresponding to the minimal expected misclassification cost: $${\widehat{y}}_j=\underset{k=1,\mathrm{...},K}{\text{argmin}}{\gamma }_{jk}.$$ Using C, identify the cost incurred (cj) for making the prediction. The weighted average of the minimal expected misclassification cost loss is $$L={\displaystyle \sum _{j=1}^n{w}_j{c}_j}.$$
Quadratic loss	"quadratic"	$$L={\displaystyle \sum _{j=1}^n{w}_j{\left(1-m_j\right)}^2}.$$

If you use the default cost matrix (whose element value is 0 for correct classification and 1 for incorrect classification), then the loss values for "classifcost", "classiferror", and "mincost" are identical. For a model with a nondefault cost matrix, the "classifcost" loss is equivalent to the "mincost" loss most of the time. These losses can be different if prediction into the class with maximal posterior probability is different from prediction into the class with minimal expected cost. Note that "mincost" is appropriate only if classification scores are posterior probabilities.

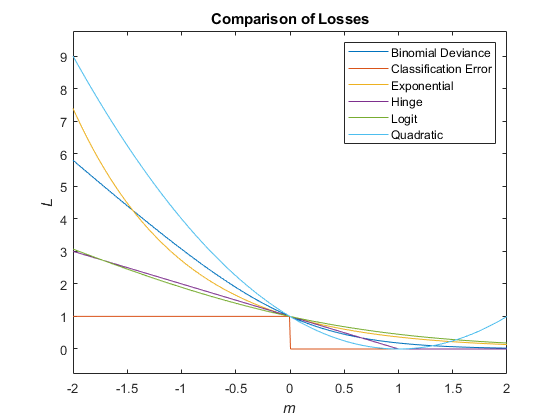
This figure compares the loss functions (except "classifcost", "crossentropy", and "mincost") over the score m for one observation. Some functions are normalized to pass through the point (0,1).

Extended Capabilities

Automatic Parallel Support

Accelerate code by automatically running computation in parallel using Parallel Computing Toolbox™.

To run in parallel, set the UseParallel name-value argument to true in the call to this function.

For more general information about parallel computing, see Run MATLAB Functions with Automatic Parallel Support (Parallel Computing Toolbox).

Version History

Introduced in R2012b

R2022a: oobLoss returns a different value for a model with a nondefault cost matrix

If you specify a nondefault cost matrix when you train the input model object, the oobLoss function returns a different value compared to previous releases.

The oobLoss function uses the observation weights stored in the W property. Also, the function uses the cost matrix stored in the Cost property if you specify the LossFun name-value argument as "classifcost" or "mincost". The way the function uses the W and Cost property values has not changed. However, the property values stored in the input model object have changed for a model with a nondefault cost matrix, so the function might return a different value.

For details about the property value change, see Cost property stores the user-specified cost matrix.

If you want the software to handle the cost matrix, prior probabilities, and observation weights in the same way as in previous releases, adjust the prior probabilities and observation weights for the nondefault cost matrix, as described in Adjust Prior Probabilities and Observation Weights for Misclassification Cost Matrix. Then, when you train a classification model, specify the adjusted prior probabilities and observation weights by using the Prior and Weights name-value arguments, respectively, and use the default cost matrix.