衝突のないロボットに対するバリア証明書の制約の適用

この例では、Barrier Certificate Enforcement ブロックを使用して衝突のないロボットに対するバリア証明書の制約を適用する方法を示します。

概要

この例では、ロボットの目標は互いに衝突せずにターゲット位置に到達することです ([1])。ロボット ダイナミクスは x-y 平面で double の積分器によってモデル化されます。各ロボットには 4 つの状態 (x 位置、y 位置、x 速度、y 速度) と 2 つの制御変数 (x 加速度と y 加速度) があります。速度は [-2, 2] m/s に制約され、加速度は [-10, 10] m/s^2 に制約されます。PID コントローラーはロボットがターゲット位置に到達するように設計されています。衝突回避はバリア証明書の制約を適用することによって実現します。

Simulink® モデルを開きます。

mdl = 'twoRobotsCBF';
open_system(mdl);

コントローラー設計

各ロボットにはターゲット位置に移動するための独自のコントローラーがあります。この例では、コントローラーが PID タイプのコントローラーとして実装されています。

シミュレーションを実行し、結果を確認します。

constrained = 0;
sim(mdl);

この Figure では、ロボット 1 (緑) はターゲット位置 [4.9, 4.8] m に到達し、ロボット 2 はターゲット位置 [0, 0] m に到達します。コントローラーにより、制御対象ロボットはそれぞれのターゲット位置に正常に移動します。

Two robots、visualization サブシステムで距離範囲を開きます。2 台のロボットは 1.3 秒前後で互いに衝突します。

バリア証明書の制約

衝突回避に対する制約では、2 台のロボットが互いに接近している場合、その 2 台のロボット $\mathit{i}$ と $\mathit{j}$ 間の距離が指定されたしきい値を超えたまま維持されるようにします ([1])。バリア証明書は以下のように求められます。

$$h(x)=\sqrt{2{\alpha }_{sum}(\Vert ▵p_{ij}\Vert -D_s)}+\frac{▵p_{ij}^T▵v_{ij}}{\Vert ▵p_{ij}\Vert }$$.

ここでは、変数は次のとおりです。

• 両方のロボットからの最大制動力 — ${\alpha }_{\mathrm{sum}}=20$

• ロボット間の最小距離 — ${\mathit{D}}_{\mathit{s}}=0.7$

• 位置誤差のベクトル — $$▵p_{ij}=p_i-p_j$$

• 速度誤差のベクトル — $$▵v_{ij}=v_i-v_j$$

状態 $\mathit{x}={\left[{\mathit{p}}_{\mathit{i}},{\mathit{p}}_{\mathit{j}},{\mathit{v}}_{\mathit{i}},{\mathit{v}}_{\mathit{j}}\right]}^{\mathit{T}}$ に対する $\mathit{h}\left(\mathit{x}\right)$ の偏導関数は $\mathit{q}\left(\mathit{x}\right)$ によって表され、解析結果は barrierGradFcn2Robots スクリプトによって求められます。

Barrier Certificate Enforcement ブロックは形式 $$\underset{}{\overset{\dot{}}{x}}=f(x)+g(x)u$$ のダイナミクスを受け入れます。この例では、次のようになります。

$\mathit{f}\left(\mathit{x}\right)=\left[\begin{array}{cccc}0& 0& \mathit{I}& 0\\ 0& 0& 0& \mathit{I}\\ 0& 0& 0& 0\\ 0& 0& 0& 0\end{array}\right]\mathit{x}$ および $\mathit{g}\left(\mathit{x}\right)=\left[\begin{array}{cc}0& 0\\ 0& 0\\ \mathit{I}& 0\\ 0& \mathit{I}\end{array}\right]$

各要素は 2 行 2 列の行列です。

バリア証明書の制約を使用した衝突のないコントローラーのシミュレーション

制約の実装を表示するには、Constraint、Constrained サブシステムを開きます。

constrained = 1;

モデルを実行する前に Figure を閉じます。

f = findobj('Name','Two robots');
close(f)

モデルを実行し、シミュレーション結果を確認します。2 台のロボットは、接近しすぎると互いに避けます。

sim(mdl);

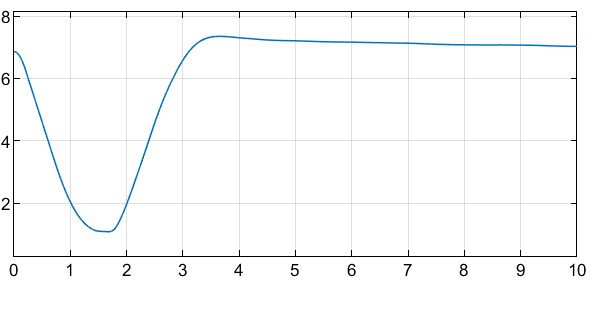
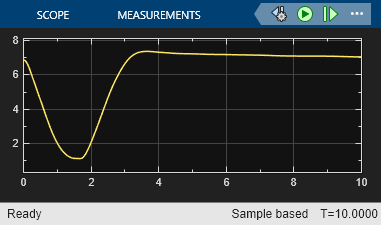
2 台のロボット間の距離はしきい値 ${\mathit{D}}_{\mathit{s}}=0.7$ を超えて維持されます。

Barrier Certificate Enforcement ブロックによって、2 台のロボットが衝突なしでそれぞれのターゲット位置に到達するように、正常に制御動作が制約されています。

bdclose(mdl)
f = findobj('Name','Two robots');
close(f)

参考文献

[1] Wang, Li, Aaron D. Ames, and Magnus Egerstedt. "Safety Barrier Certificates for Collisions-Free Multirobot Systems." IEEE Transactions on Robotics 33, no. 3 (June 2017): 661–74. https://doi.org/10.1109/TRO.2017.2659727.

参考

Barrier Certificate Enforcement

関連するトピック

• 制御設計へのバリア証明書の適用
• アダプティブ クルーズ コントロールに対するバリア証明書の制約の適用
• PID コントローラーに対するバリア証明書の制約の適用
• 衝突のないマルチロボット システムに対するバリア証明書の制約の適用