HL-20 の自動操縦の姿勢制御 - SISO 設計
これは、HL-20 機体用の飛行制御システムの設計と調整に関する例のシリーズのパート 3 です。このパートでは、機体のロール、ピッチ、およびヨーを制御するための従来の SISO アーキテクチャを調整する方法について説明します。
背景
この例ではNASA HL-20 揚力体機体 (Aerospace Blockset)から応用した HL-20 モデルを使用します。詳細については、シリーズのパート 1 (HL-20 機体の平衡化と線形化) を参照してください。航空機の姿勢を制御する自動操縦には 3 つの内側のループと 3 つの外側のループが含まれます。
パート 2 (HL-20 の自動操縦における角速度の制御) では、角速度 p、q、r を制御する内側のループを閉じる方法を示しました。以下のコマンドは該当する手順をまとめたものです。これにより、Simulink® モデルを操作するための slTuner インターフェイス ST0 が作成されて構成されます。
load_system('csthl20_control') CTYPE = 2; % Select SISO architecture HL20recapPart2 ST0
slTuner tuning interface for "csthl20_control":
No tuned blocks. Use the addBlock command to add new blocks.
9 Analysis points:
--------------------------
Point 1: Signal "da;de;dr", located at 'Output Port 1' of csthl20_control/Flight Control System/Controller
Point 2: Signal "pqr", located at 'Output Port 2' of csthl20_control/HL20 Airframe
Point 3: 'Output Port 1' of csthl20_control/Flight Control System/Alpha_deg
Point 4: 'Output Port 1' of csthl20_control/Flight Control System/Beta_deg
Point 5: 'Output Port 1' of csthl20_control/Flight Control System/Phi_deg
Point 6: 'Output Port 1' of csthl20_control/Flight Control System/Controller/Classical/Demands
Point 7: Signal "p_demand", located at 'Output Port 1' of csthl20_control/Flight Control System/Controller/Classical/Roll-off1
Point 8: Signal "q_demand", located at 'Output Port 1' of csthl20_control/Flight Control System/Controller/Classical/Roll-off2
Point 9: Signal "r_demand", located at 'Output Port 1' of csthl20_control/Flight Control System/Controller/Classical/Roll-off3
No permanent openings. Use the addOpening command to add new permanent openings.
Properties with dot notation get/set access:
Parameters : []
OperatingPoints : [] (model initial condition will be used.)
BlockSubstitutions : [3x1 struct]
Options : [1x1 linearize.SlTunerOptions]
Ts : 0
外側ループの調整の設定
ここでは、ロール (phi)、迎角 (alpha)、横滑り角 (beta) を制御する 3 つのゲイン スケジュール PI ループに焦点を移します。これらのループは 1 つずつ調整することができます (3 つのループと 40 の操作条件で 120 の設計点になります)。あるいは pidtune を使用して、特定のターゲット帯域幅と位相余裕の要件に対して PI ゲインをバッチ モードで調整することも可能です。両方のアプローチで次の点に注意してください。
ループの相互作用を考慮するのが難しい。
各設計点で得られたゲインが一貫性に欠け、操作点全体での平滑化が必要になる可能性がある。
代替のアプローチとして "ゲイン曲面調整" [1] という概念があります。これはゲイン スケジュール P(alpha,beta) および I(alpha,beta) を多項式曲面としてパラメーター化し、systune を使って多項式の係数を調整する方法です。このアプローチはすべての操作点を同時に処理するため、特に安定余裕の考慮において、ループの相互作用を計算に入れることができます。ここではこのアプローチを紹介します。
外側のループを調整するには、内側のループを閉じて、それぞれの (alpha,beta) 条件で外側のループによって認識される "プラント" の線形化モデルを取得しなければなりません。対応する伝達関数を slTuner に計算させることもできますが、その場合は内側のループのゲイン Kp、Kq、Kr が既定の操作条件におけるそれぞれの値に実質的に固定されてしまいます。線形化を正しく行うには、これらのゲインが (alpha,beta) に従って変化することを slTuner に指定しなければなりません。そのためには、ここでもブロック置換が一番簡単な方法です。Kp を可変としてマークするには、誤差信号を Kp で乗算するために使用される Product ブロックを見つけ、これを (alpha,beta) の各条件ごとに 1 つのゲインをもつゲインの配列に置き換えます。
ProductBlk = 'csthl20_control/Flight Control System/Controller/Classical/Product1'; BlockSub4 = struct('Name',ProductBlk,'Value',[0 ss(Kp)]);
このブロック線形化を行うと誤差信号が上で計算した可変量 Kp で乗算されることは、簡単に検証できます。同様に、Kq と Kr の対応する Product ブロックを可変ゲインで置き換えます。
ProductBlk = 'csthl20_control/Flight Control System/Controller/Classical/Product3'; BlockSub5 = struct('Name',ProductBlk,'Value',[0 ss(Kq)]); ProductBlk = 'csthl20_control/Flight Control System/Controller/Classical/Product4'; BlockSub6 = struct('Name',ProductBlk,'Value',[0 ss(Kr)]); ST0.BlockSubstitutions = [ST0.BlockSubstitutions ; BlockSub4 ; BlockSub5 ; BlockSub6];
これで、モデルの初期のゲイン スケジュール設定に対する角度応答をプロットできます。
T0 = getIOTransfer(ST0,'Demand',{'Phi_deg','Alpha_deg','Beta_deg'}); step(T0,6)

調整目標
基本的な制御目的には帯域幅 (応答時間) と安定余裕が含まれます。"MinLoopGain" および "MaxLoopGain" の目標を使用して、外側のループのゲイン交差を 0.5 ~ 5 rad/s の間に設定します。すべてのループ変数が度単位で表されるので、追加のスケーリングは必要ありません。
R1 = TuningGoal.MinLoopGain({'Phi_deg','Alpha_deg','Beta_deg'},0.5,1);
R1.LoopScaling = 'off';
R2 = TuningGoal.MaxLoopGain({'Phi_deg','Alpha_deg','Beta_deg'},tf(50,[1 10 0]));
R2.LoopScaling = 'off';"Margins" 目標を使用して、各ループ内およびループ間に適切な安定余裕を設定します。この目標はディスク余裕の概念に基づくもので、3 つすべてのループでゲインと位相が同時に変動する場合であっても安定性が保証されます。極端な方向 ((alpha,beta) グリッドの隅) では 7 dB および 40 度というターゲット余裕を得ることが難しいため、可変目標を使って隅でのゲイン余裕と位相余裕の要件を緩和させます。
% Gain margins vs (alpha,beta) GM = [... 6 6 6 6 6 6 6 7 6 6 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 7 6 6 7 6 6 6 6 6 6 6]; % Phase margins vs (alpha,beta) PM = [... 40 40 40 40 40 40 40 45 40 40 45 45 45 45 45 45 45 45 45 45 45 45 45 45 45 45 45 45 45 45 40 40 45 40 40 40 40 40 40 40]; % Create varying goal FH = @(gm,pm) TuningGoal.Margins('da;de;dr',gm,pm); R3 = varyingGoal(FH,GM,PM);
ゲイン スケジュール調整
外側のループ用に P と I のゲイン スケジュールを調整するには、3 つの MATLAB Function ブロックと 3 つのルックアップ テーブルを調整可能としてマークします。
TunedBlocks = {'P phi','P alpha','P beta','I phi','I alpha','I beta'};
ST0.addBlock(TunedBlocks)調整後のゲイン スケジュールを alpha と beta の多項式曲面としてパラメーター化します。ここでは比例ゲインに 2 次曲面を使用し、積分ゲインに多重線形曲面を使用します。
% Grid of (alpha,beta) design points alpha_vec = -10:5:25; % Alpha Range beta_vec = -10:5:10; % Beta Range [alpha,beta] = ndgrid(alpha_vec,beta_vec); SG = struct('alpha',alpha,'beta',beta); % Proportional gains alphabetaBasis = polyBasis('canonical',2,2); P_PHI = tunableSurface('Pphi', 0.05, SG, alphabetaBasis); P_ALPHA = tunableSurface('Palpha', 0.05, SG, alphabetaBasis); P_BETA = tunableSurface('Pbeta', -0.05, SG, alphabetaBasis); ST0.setBlockParam('P phi',P_PHI); ST0.setBlockParam('P alpha',P_ALPHA); ST0.setBlockParam('P beta',P_BETA); % Integral gains alphaBasis = @(alpha) alpha; betaBasis = @(beta) abs(beta); alphabetaBasis = ndBasis(alphaBasis,betaBasis); I_PHI = tunableSurface('Iphi', 0.05, SG, alphabetaBasis); I_ALPHA = tunableSurface('Ialpha', 0.05, SG, alphabetaBasis); I_BETA = tunableSurface('Ibeta', -0.05, SG, alphabetaBasis); ST0.setBlockParam('I phi',I_PHI); ST0.setBlockParam('I alpha',I_ALPHA); ST0.setBlockParam('I beta',I_BETA);
各ゲイン曲面は、ベースライン設計によって示された固定値に初期化された点に注意してください。一般に、ゼロやランダムの初期点から開始することは推奨されません。これは、問題の難度によって関連性の低い局所的最小値に留まってしまう可能性が高くなるためです。代わりに、より効果的な方法として、ゲインの固定 (スケジュールされない) セットを設計点の完全なセット (または関連するサブセット) に対して調整することをお勧めします。そのような "ロバスト設計" では、通常ゲイン曲面調整の良好な開始点を得ることができます。
これで、systune を使用して 6 つのゲイン曲面を 3 つの調整目標に対して調整できます。
ST = systune(ST0,[R1 R2 R3]);
Final: Soft = 1.03, Hard = -Inf, Iterations = 41
最終目的値は 1 に近いので、調整目標は実質的に満たされます。閉ループ角度応答をプロットしてベースライン設計と比較します。
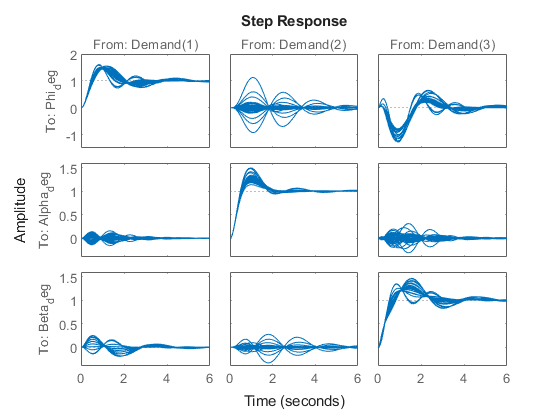
T = getIOTransfer(ST,'Demand',{'Phi_deg','Alpha_deg','Beta_deg'}); step(T0,T,6) legend('Baseline','Tuned','Location','SouthEast')

この結果は、ロール角と横滑り角の応答における振動が少なく、相互干渉の量が削減されたベースラインと同様になります。viewSurf を使用して調整後のゲイン曲面を検査します。
TV = getTunedValue(ST);
clf
% NOTE: setBlockValue updates each gain surface with the tuned coefficients in TV
subplot(3,2,1)
viewSurf(setBlockValue(P_PHI,TV))
subplot(3,2,3)
viewSurf(setBlockValue(P_ALPHA,TV))
subplot(3,2,5)
viewSurf(setBlockValue(P_BETA,TV))
subplot(3,2,2)
viewSurf(setBlockValue(I_PHI,TV))
subplot(3,2,4)
viewSurf(setBlockValue(I_ALPHA,TV))
subplot(3,2,6)
viewSurf(setBlockValue(I_BETA,TV))
検証
この設計をさらに詳しく検証するには、調整後のゲイン曲面を Simulink モデルにプッシュします。
writeBlockValue(ST)
3 つのルックアップ テーブル ブロック "I phi"、"I alpha"、"I beta" については、writeBlockValue がテーブル ブレークポイントでゲイン曲面をサンプリングして、モデル ワークスペースにあるテーブル データを更新します。MATLAB Function ブロック "P phi"、"P alpha"、"P beta" については、writeBlockValue がゲイン曲面方程式の MATLAB® コードを生成します。たとえば、"P phi" ブロックのコードは次のようになります。

Simulink Coder™ はこの MATLAB コードを効率的な組み込み C コードに自動的に変換します。ルックアップ テーブルと MATLAB Function ブロックのどちらを使用するかはアプリケーションによって異なります。MATLAB Function のオプションでは、ゲインを alpha と beta の関数として確実に滑らかに変化させる (ブレークポイントでのねじれをなくす) ことが可能です。さらに、格納が必要なのはゲイン曲面の多項式曲面の係数だけなので、メモリ効率も向上します。一方で、特定の (alpha,beta) 点でゲインを評価する場合は、ルックアップ テーブルを使用するよりも多くの操作が必要となることがあります。また、ゲインをさらに調整する場合もルックアップ テーブルの方が簡単です。
ゲインを Simulink にプッシュすると自動操縦の調整が完了し、着陸アプローチ時の動作をシミュレートすることができます。

性能は十分ですが、線形応答から軸間に相互干渉が多く見られることがわかり、(alpha,beta) の範囲の隅の点において安定余裕のターゲットを完全には達成できていません。phi、alpha、beta の 3 つの測定値すべてを組み合わせて曲面偏向角を計算する MIMO アーキテクチャを使用する利点について検討する余地があります。このシリーズのパート 4 (HL-20 の自動操縦の姿勢制御 - MIMO 設計) では、この点について詳しく見ることにします。
参考文献
[1] P. Gahinet and P. Apkarian, "Automated tuning of gain-scheduled control systems," in Proc. IEEE Conf. Decision and Control, Dec 2013.