HL-20 の自動操縦の姿勢制御 - MIMO 設計

この例では次を使用します。

これは、HL-20 機体用の飛行制御システムの設計と調整に関する例のシリーズのパート 4 です。このパートでは、機体のロール、ピッチ、およびヨーを制御するための MIMO PI アーキテクチャを調整する方法について説明します。

背景

この例ではNASA HL-20 Lifting Body Airframe (Aerospace Blockset)から応用した HL-20 モデルを使用します。詳細については、シリーズのパート 1 (HL-20 機体の平衡化と線形化) を参照してください。パート 2 と 3 では HL-20 自動操縦のクラシックな SISO アーキテクチャの内側のループを閉じて外側のループを調整する方法を示しました。詳細については、HL-20 の自動操縦における角速度の制御およびHL-20 の自動操縦の姿勢制御 - SISO 設計を参照してください。この例では、外側のループを処理するために MIMO アーキテクチャに切り替えることの利点について考えます。

このアーキテクチャでは、pitch、alpha、beta 用の 3 つの PI ループを、pitch、alpha、beta の測定値を組み合わせて内側のループの設定点 p_demand、q_demand、r_demand を計算する 3 入力 3 出力の PI コントローラーで置き換えます。直感的には、このアーキテクチャの方が軸間の相互干渉を正しく抑えることができるように思えます。P と I のゲインは alpha と beta の関数としてスケジュールされる 3 行 3 列の行列であることに注意してください。

まず、モデルを読み込んで CTYPE を 3 に設定し、Controller ブロックの MIMO バリアントを選択します。パート 2 の手順を再実行して内側のループを閉じます (設計のこの部分に変更はありません)。これにより、Simulink モデルを操作するための slTuner インターフェイス ST0 が作成されて構成されます。

load_system('csthl20_control')
CTYPE = 3;  % MIMO architecture
HL20recapPart2

ST0

 
slTuner tuning interface for "csthl20_control":

No tuned blocks. Use the addBlock command to add new blocks.
9 Analysis points: 
--------------------------
Point 1: Signal "da;de;dr", located at 'Output Port 1' of csthl20_control/Flight Control System/Controller
Point 2: Signal "pqr", located at 'Output Port 2' of csthl20_control/HL20 Airframe
Point 3: 'Output Port 1' of csthl20_control/Flight Control System/Alpha_deg
Point 4: 'Output Port 1' of csthl20_control/Flight Control System/Beta_deg
Point 5: 'Output Port 1' of csthl20_control/Flight Control System/Phi_deg
Point 6: 'Output Port 1' of csthl20_control/Flight Control System/Controller/MIMO/Demands
Point 7: Signal "p_demand", located at 'Output Port 1' of csthl20_control/Flight Control System/Controller/MIMO/Roll-off1
Point 8: Signal "q_demand", located at 'Output Port 1' of csthl20_control/Flight Control System/Controller/MIMO/Roll-off2
Point 9: Signal "r_demand", located at 'Output Port 1' of csthl20_control/Flight Control System/Controller/MIMO/Roll-off3
 
No permanent openings. Use the addOpening command to add new permanent openings.
Properties with dot notation get/set access:
      Parameters         : [] 
      OperatingPoints    : [] (model initial condition will be used.)
      BlockSubstitutions : [3x1 struct]
      Options            : [1x1 linearize.SlTunerOptions]
      Ts                 : 0

外側ループの調整の設定

SISO 設計 (HL-20 の自動操縦の姿勢制御 - SISO 設計) の場合と同様に、最初の手順ではそれぞれの (alpha,beta) 条件で外側のループによって認識される "プラント" の線形化モデルを取得します。内側のループのゲイン Kp、Kq、Kr が (alpha,beta) によって変化するという事実を考慮するため、"MIMO/Product" ブロックをその線形の等価物である次の対角ゲイン行列に置き換えます。

$\left( \begin{array}{ccc} Kp(\alpha,\beta) & 0 & 0 \\ 0 & Kq(\alpha,\beta) & 0 \\
0 & 0 & Kr(\alpha,\beta) \end{array} \right) .$

Blk = 'csthl20_control/Flight Control System/Controller/MIMO/Product';
Subs = [zeros(3) append(ss(Kp),ss(Kq),ss(Kr))];
BlockSub4 = struct('Name',Blk,'Value',Subs);

ST0.BlockSubstitutions = [ST0.BlockSubstitutions ; BlockSub4];

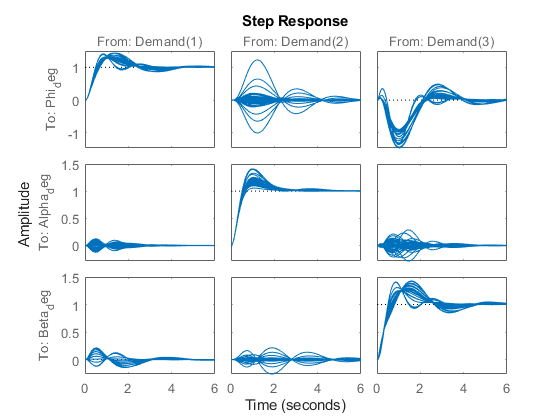
ゲインスケジュール "P" および "I" が定数対角行列 diag([0.05, 0.05, -0.05]) に初期化されます。これらの初期設定の角度応答をプロットします。

T0 = getIOTransfer(ST0,'Demand',{'Phi_deg','Alpha_deg','Beta_deg'});
step(T0,6)

調整目標

MIMO ゲインスケジュールを調整するには、次の 3 つの調整目標を使用します。

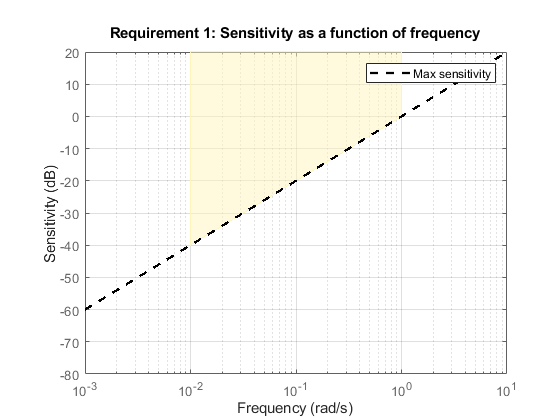
目的の帯域幅 (応答時間) を指定して低周波数でのデカップリングを最大化する "Sensitivity" 目標。

s = tf('s');
R1 = TuningGoal.Sensitivity({'Phi_deg','Alpha_deg','Beta_deg'},s);
R1.Focus = [1e-2 1];
R1.LoopScaling = 'off';

viewGoal(R1)

角度要求から角度応答への閉ループ伝達に適用する "Gain" 制約。適切なロールオフを課してオーバーシュートを制限するゲインプロファイルが選択されます (これは交差近傍の隆起に関係があります)。

MaxGain = 1.2 * (10/(s+10))^2;  % max gain profile
R2 = TuningGoal.Gain('Demands',{'Phi_deg','Alpha_deg','Beta_deg'},MaxGain);

viewGoal(R2)

少なくとも 7 dB のゲイン余裕と 45 度の位相余裕 (ディスク余裕の意味で) を要求する "Margins" 目標。

R3 = TuningGoal.Margins('da;de;dr',7,45);

ゲインスケジュール調整

MIMO PI コントローラーのゲインスケジュールは MIMO アーキテクチャ内の "P" ブロックと "I" ブロックにより指定されます。これらのブロックが 3 行 3 列の行列を出力し、次の MIMO 伝達関数を実装することを思い出してください。

$\left( \begin{array}{c} p_{\rm demand} \\ q_{\rm demand} \\ r_{\rm demand} \end{array} \right) =
\frac{10}{s+10} (P + I / s)
\left( \begin{array}{c} \phi_{\rm deg} \\ \alpha_{\rm deg} \\ \beta_{\rm deg} \end{array} \right).$

説明のため、MATLAB Function ブロックを使って比例ゲインスケジュールを実装し、Matrix Interpolation ブロックを使って積分ゲインスケジュールを実装することにします。Matrix Interpolation ブロックは、"Simulink Extras" ライブラリに格納された、各エントリが行列であるルックアップテーブルです。

P および I のゲインスケジュールを調整するには、slTuner インターフェイスで対応するブロックを調整可能としてマークします。

TunedBlocks = {'MIMO/P' , 'MIMO/I'};
ST0.addBlock(TunedBlocks)

調整後のゲインスケジュールを alpha と beta の多項式曲面としてパラメーター化します。再び比例ゲインに 2 次曲面を使用し、積分ゲインに多重線形曲面を使用します。

% Grid of (alpha,beta) design points
alpha_vec = -10:5:25;	 % Alpha Range
beta_vec = -10:5:10;     % Beta Range
[alpha,beta] = ndgrid(alpha_vec,beta_vec);
SG = struct('alpha',alpha,'beta',beta);

% Proportional gain matrix
alphabetaBasis = polyBasis('canonical',2,2);
P0 = diag([0.05 0.05 -0.05]);  % initial (constant) value
PS = tunableSurface('P', P0, SG, alphabetaBasis);
ST0.setBlockParam('P',PS);

% Integral gain matrix
alphaBasis = @(alpha) alpha;
betaBasis = @(beta) abs(beta);
alphabetaBasis = ndBasis(alphaBasis,betaBasis);
I0 = diag([0.05 0.05 -0.05]);
IS = tunableSurface('I', I0, SG, alphabetaBasis);
ST0.setBlockParam('I',IS);

最後に systune を使用して、6 つのゲイン曲面を 3 つの調整目標に対して調整します。

ST = systune(ST0,[R1 R2 R3]);

Final: Soft = 1.13, Hard = -Inf, Iterations = 110

目的関数の最終値から、調整目標がほぼ満たされることがわかります (調整目標はその "値" が 1 未満の場合に満たされます)。閉ループ角度応答をプロットしてベースライン設計と比較します。

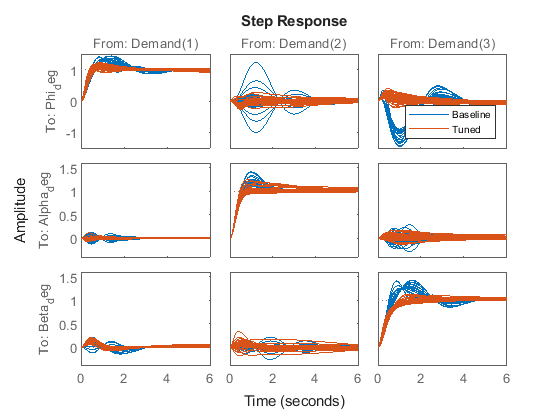
T = getIOTransfer(ST,'Demand',{'Phi_deg','Alpha_deg','Beta_deg'});
step(T0,T,6)
legend('Baseline','Tuned','Location','SouthEast')

これらの応答は、SISO 設計と比べてオーバーシュートと相互干渉が大幅に削減されていることを示しています。

検証

この設計をさらに詳しく検証するには、調整後のゲイン曲面を Simulink モデルにプッシュします。

writeBlockValue(ST)

これは、Matrix Interpolation ブロック "I" については、テーブルのブレークポイントでゲイン曲面をサンプリングし、モデルワークスペースにあるテーブルデータを更新します。MATLAB Function ブロック "P" については、ゲイン曲面方程式の MATLAB コードを生成します。このコードを表示するにはブロックをダブルクリックします。

ゲインを Simulink にプッシュすると、MIMO アーキテクチャの調整が完了し、着陸アプローチ時の動作をシミュレートすることができます。

これらの応答は、操縦全体の要求が緩いために SISO 設計のものとあまり変わりません (HL-20 の自動操縦の姿勢制御 - SISO 設計)。MIMO 設計の利点は、難度の高い操縦の方がより顕著に現れます。

参考

tunableSurface

HL-20 の自動操縦の姿勢制御 - MIMO 設計

背景

外側ループの調整の設定

調整目標

ゲイン スケジュール調整

検証

参考

関連するトピック

ゲインスケジュール調整