閉ループ制御を使ったエンジン タイミング モデル

モデルを開く

この例では、Triggered Subsystem を使用したエンジン タイミングのモデル化で説明されている開ループ エンジン モデルの閉ループ制御アルゴリズムを開発して実装する方法を示します。この例のモデル sldemo_enginewc には、負荷トルクの変化の影響が最小限に抑えられるように、高速スロットル アクチュエータを使用してエンジン速度を調節するコントローラーが含まれています。このコントローラーは離散 PI コントローラーを使って実装されます。

閉ループ モデル

コントローラーの方程式

この例では、次の方程式で記述される比例-積分 (PI) コントローラーを使用します。

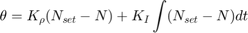
$$ \theta = K_{\rho}(N_{set}-N) + K_I \int (N_{set}-N) dt $$

$$ N_{set} = \mbox{ speed set point (rpm) } $$

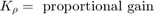
$$ K_{\rho} = \mbox{ proportional gain } $$

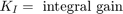
$$ K_I = \mbox{ integral gain } $$

積分項は、指令値が変化したときに定常状態スロットルを調整し、比例項は、積分器によって生じた位相遅れを補償します。方程式の積分項は離散時間近似で実装されます。業界で一般的であるように、コントローラーの実行は、エンジンのクランクシャフトの回転と同期化されます。sldemo_enginewc モデルの Controller サブシステムは、マイクロプロセッサ実装に適した、PI コントローラーを離散時間で実装する Discrete PID Controller ブロックを使用します。このコントローラーは、サブシステムがトリガーされるたびに実行されます。

モデルのシミュレーションと結果の可視化

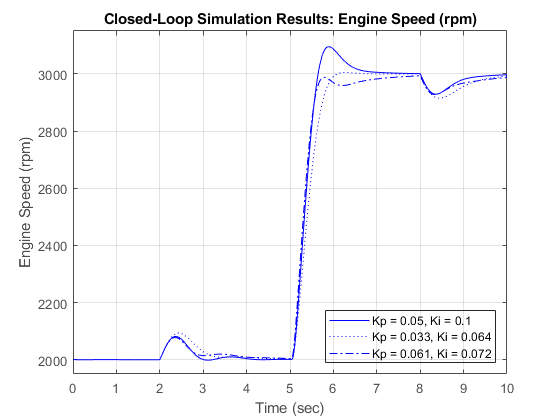
モデルは出力データをベース ワークスペースの sldemo_enginewc_output という名前のデータ セットに記録します。あるいは、Simulink® データ インスペクターを使用してログ記録された信号を可視化できます。詳細については、シミュレーション データ インスペクターを参照してください。速度指令値は、t = 5 秒で 2000 rpm から 3000 rpm にステップアップします。トルクの外乱は、開ループ モデル sldemo_engine で使用されるものと同じです。コントローラーのパラメーターは、定常偏差が 0 の、迅速な過渡応答が得られるように調整されています。定常状態応答が Ki 値と Kp 値の 3 つの異なるセットを使用して表示されるため、比例ゲイン (Kp) と積分ゲイン (Ki) がエンジン モデルの定常状態応答に与える相対的影響の把握に役立ちます。PI コントローラーは MATLAB® コマンド ラインで調整できます。

参考

| | | |

トピック

参照

[1] Crossley, P. R., and J. A. Cook. “A Nonlinear Engine Model for Drivetrain System Development.” International Conference on Control 1991. Control ’91 1991, pp. 921–25 vol.2. IEEE Xplore, DOI.org (Crossref), https://ieeexplore.ieee.org/abstract/document/98573.

[2] The Simulink Model. Developed by Ken Butts, Ford Motor Company. Modified by Paul Barnard, Ted Liefeld and Stan Quinn, MathWorks®, 1994–7."

[3] Moskwa, John J., and J. Karl Hedrick. “Automotive Engine Modeling for Real Time Control Application.” 1987 American Control Conference, 1987, pp. 341–46. IEEE Xplore, DOIː 10.23919/ACC.1987.4789343.

[4] Powell, B. K., and J. A. Cook. “Nonlinear Low Frequency Phenomenological Engine Modeling and Analysis.” 1987 American control conference, 1987, pp. 332–40. IEEE Xplore, DOIː 10.23919/ACC.1987.4789342.

[5] Weeks, Robert W., and John J. Moskwa. “Automotive Engine Modeling for Real-Time Control Using MATLAB/SIMULINK.” SAE transactions, vol. 104, 1995, pp. 295–309. JSTOR, https://www.jstor.org/stable/44473229.