高迎角のピッチモード制御の設計

この例では次を使用します。

Simulink を使用した制御設計

この例では、Control System Toolbox™ と Simulink® Control Design™ を使用して Simulink を操作し、航空機のデジタルピッチ制御を設計する方法を示しています。この例では、この航空機を最小限の作業負荷で高迎角で操作できるようにコントローラーを設計します。

この例では、高迎角コントローラーのデジタル自動操縦設計の第 1 段階について説明します。この例のすべてを実行するには、Control System Toolbox、Simulink Control Design、Simulink、Simulink Coder™ を保有していなければなりません。ただし、これらの製品のうちもっていないものがある場合でも、MATLAB® エディターのセルの実行モードを使用して、この例の一部を実行することが可能です。

以下に、航空機の Simulink モデルを示します。Controllers ブロック内の制御システムをモデルで切り替えてアナログ応答を確認した後、Control System Toolbox の線形時不変 (LTI) オブジェクトで作成された設計に切り替えることができます。オンボードフライトコンピューターに組み込まれるアルゴリズムと同様のアナログ設計の離散的実装であるコントローラーも含まれています。少し時間をとって、モデルを調べます。

図 1: 航空機飛行制御システムの Simulink モデル

平衡化と線形化

Simulink Control Design ソフトウェアを使用してモデルを線形化できます。モデルを対話的に線形化するには、[モデル線形化器] アプリを使用します。このアプリを開くには、Simulink エディターで、[アプリ] タブの [制御システム] で [モデル線形化器] をクリックします。また、関数 linearize を使用したモデルのプログラムによる線形化もできます。

slexAircraftPitchControlAutopilot モデルを開きます。

線形化されたモデルパラメーターを表示するには、以下を実行します。

apmdl = 'slexAircraftPitchControlAutopilot';
open_system(apmdl)
op = operpoint(apmdl);
io = getlinio(apmdl);
contap = linearize(apmdl,op,io)

contap =
 
  A = 
                 Alpha-sensor  Pitch Rate L  Proportional  Stick Prefil
   Alpha-sensor        -2.526             0             0             0
   Pitch Rate L             0        -4.144             0             0
   Proportional         -1.71        0.9567             0            10
   Stick Prefil             0             0             0           -10
 
  B = 
                 Alpha Sensed         Stick      q Sensed
   Alpha-sensor             1             0             0
   Pitch Rate L             0             0             1
   Proportional             0             0       -0.8156
   Stick Prefil             0             1             0
 
  C = 
        Alpha-sensor  Pitch Rate L  Proportional  Stick Prefil
   Sum         2.986         -1.67        -3.864        -17.46
 
  D = 
        Alpha Sensed         Stick      q Sensed
   Sum             0             0         1.424
 
Continuous-time state-space model.

図 2: オリジナルのアナログ自動操縦

線形時不変 (LTI) システム

線形モデルの作成に使用できる LTI オブジェクトには、

状態空間 (SS) オブジェクト、伝達関数 (TF) オブジェクト、零点-極-ゲイン (ZPG) オブジェクトの 3 つのタイプがあります。

変数 contap は状態空間オブジェクトです。次に、他のコマンドを使用して他のいずれかのタイプのオブジェクトを取得できます。オブジェクトを MATLAB で作成する場合、*、+、- などの演算を使用してそのオブジェクトを操作できます。これは MATLAB 演算子の "オーバーロード" と呼ばれます。独自のオブジェクトを作成し、contap オブジェクトを使用して加算や乗算などを実行した場合に何が起こるのかを確認してみてください。

LTI オブジェクトに何が保存されているのかを確認するには、たとえば「get(contap)」または「contap.InputName」と入力します。

零点/極/ゲイン伝達関数を表示するには、以下を実行します。

contap = tf(contap);
contap = zpk(contap)

contap =
 
  From input "Alpha Sensed" to output "Sum":
  2.9857 (s+2.213)
  ----------------
    s (s+2.526)
 
  From input "Stick" to output "Sum":
  -17.46 (s+2.213)
  ----------------
      s (s+10)
 
  From input "q Sensed" to output "Sum":
  1.424 (s+2.971) (s+2.213)
  -------------------------
         s (s+4.144)
 
Continuous-time zero/pole/gain model.

ゼロ次ホールドを使用した離散化コントローラー

次に、LTI オブジェクトを使用してデジタル自動操縦が設計され、アナログ自動操縦がこのデジタル自動操縦に置き換えられます。アナログシステムは、contap と呼ばれる LTI オブジェクト (CONtinuous AutoPilot) にコーディングされます。

デジタル自動操縦の作成においてはまず、ゼロ次ホールドを 0.1 秒のサンプル時間で使用してみます。離散オブジェクトのタイプ (ss、tf、または zpk) は保持されます。

システムの位相が操縦かん入力と攻撃センサーの角度について 3 rad/sec からサンプル周波数の半分 (黒い縦線) まで一致していないことは、以下のボード線図から明らかです。この設計の応答は、アナログシステムよりも劣っています。Simulink モデルに移動し、シミュレーションを開始します (スコープウインドウが見えることを確認)。シミュレーションの実行中、Analog または Digital というラベルの付いた手動スイッチをダブルクリックします。

ボード線図を解釈することによって到達した結論が、このシミュレーションで検証されていますか?

discap = c2d(contap, 0.1, 'zoh');
get(discap)
bode(contap,discap)

                Z: {[0.8016]  [0.8039]  [2x1 double]}
                P: {[2x1 double]  [2x1 double]  [2x1 double]}
                K: [0.2943 -1.2458 1.4240]
    DisplayFormat: 'roots'
         Variable: 'z'
          IODelay: [0 0 0]
       InputDelay: [3x1 double]
      OutputDelay: [0]
        InputName: {3x1 cell}
        InputUnit: {3x1 cell}
       InputGroup: [1x1 struct]
       OutputName: {'Sum'}
       OutputUnit: {''}
      OutputGroup: [1x1 struct]
            Notes: [0x1 string]
         UserData: []
             Name: ''
               Ts: [0.1000]
         TimeUnit: 'seconds'
     SamplingGrid: [1x1 struct]

図 3: アナログコントローラーとゼロ次ホールドコントローラーを比較したボード線図

Tustin (双線形) 離散化

次に、別の変換手法を試してみます。Tustin 変換を使用できます。コマンドウィンドウで、上記のコマンドを入力します。

ここでもシステムの位相は 3 rad/sec からサンプル周波数の半分まで一致していませんが、それでも Tustin 変換の方がうまくいっていることは明らかです。シミュレーションでは、設計どおり LTI オブジェクトが使用されます。このオブジェクトがどのように使用されるのかを確認するには、ブラウザーを使用するかアイコンをダブルクリックすることにより、Controllers サブシステムを参照します。LTI オブジェクトがワークスペースから検出されます。ブロック内で使用されているオブジェクト名を、ワークスペース内の任意の LTI オブジェクトに変更できます。

アナログ設計の Tustin 離散化 "discap1" を使用してみます。

discap1 = c2d(contap,0.1,'tustin');
bode(contap,discap,discap1)

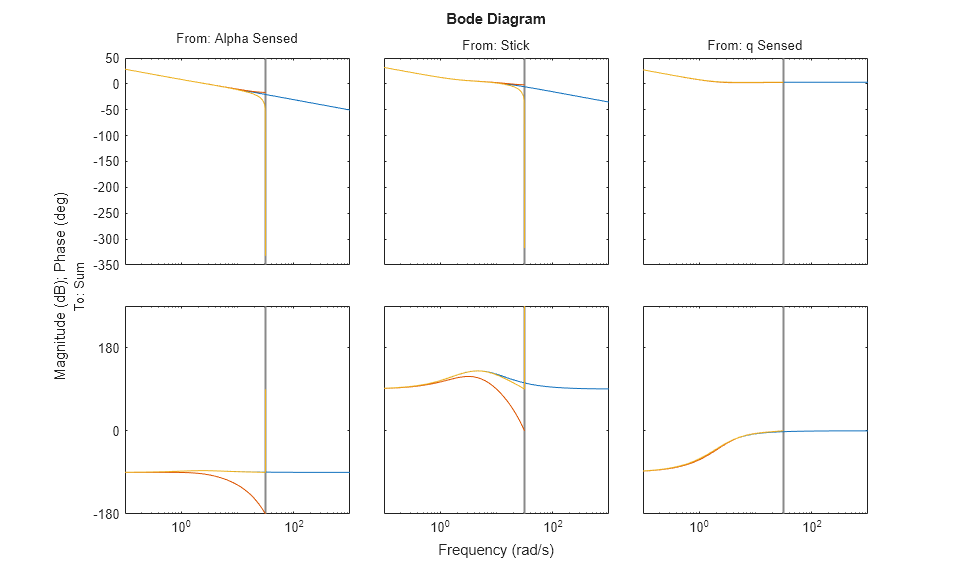
図 4: アナログコントローラーと 0.1 秒の Tustin コントローラーを比較したボード線図

サンプル時間の選択

解析から今までのところでは、ゼロ次ホールドよりも双一次変換の方がうまくいっています。離散システムを使用してサンプル周波数の半分でアナログシステムの性能を追跡するには、0.1 秒というサンプル時間は遅すぎるようです。

そこで、双一次変換でサンプル時間を 0.05 秒としてアナログ設計を変換します。

discap = c2d(contap,0.05,'tustin')
bode(contap,discap)

discap =
 
  From input "Alpha Sensed" to output "Sum":
  0.074094 (z-0.8951) (z+1)
  -------------------------
      (z-1) (z-0.8812)
 
  From input "Stick" to output "Sum":
  -0.36852 (z-0.8951) (z+1)
  -------------------------
        (z-1) (z-0.6)
 
  From input "q Sensed" to output "Sum":
  1.4629 (z-0.8617) (z-0.8951)
  ----------------------------
        (z-1) (z-0.8123)
 
Sample time: 0.05 seconds
Discrete-time zero/pole/gain model.

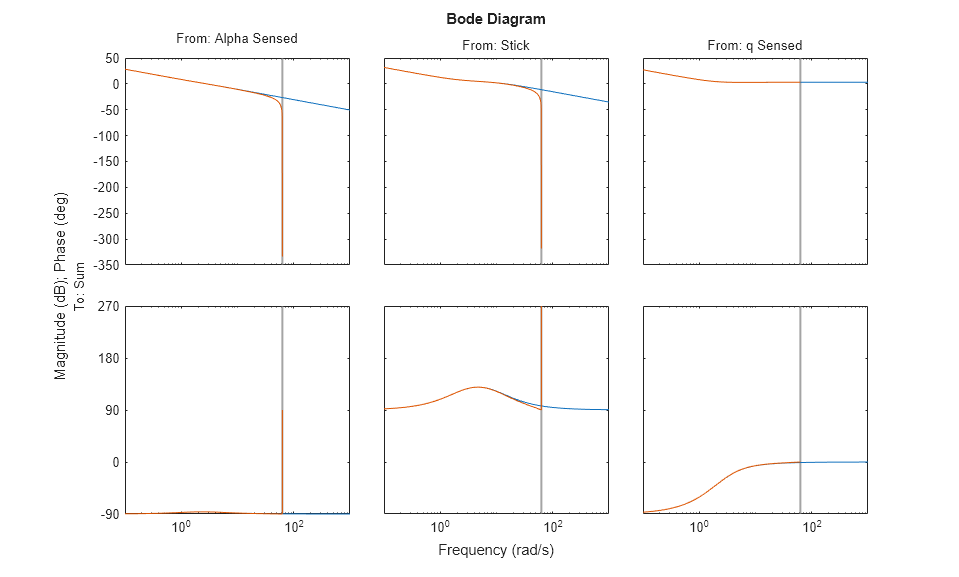
図 5: アナログコントローラーと 0.05 秒の Tustin コントローラーを比較したボード線図

実用面での考慮事項

実際的な設計と思われるものが出来上がったところで、これを、それまで線形解析で無視されていた必須要素のいくつかを含むような形式で実装する必要があります。たとえば、Controllers サブシステムにあるアナログ自動操縦を調べると、アクチュエータの飽和時の積分動作によるワインドアップを防止する何らかのロジックがあります。

AnalogControl サブシステムを開きます。

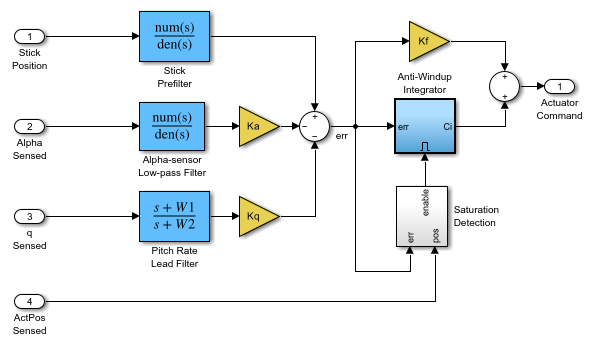
図 6: AnalogControl サブシステム

完全な設計の実装

積分動作によるワインドアップは、対策の必要な実用上の問題の 1 つにすぎません。他にも、測定点で入る可能性のある、エイリアシングされた高周波信号を除去する必要があります。組み込みアプリケーションでの信号の測定に典型的に使用されるアナログデジタルコンバーター (ADC) デバイスをモデル化するサンプルブロックとホールド (ZOH) ブロックの前にアナログフィルターを指定することで、エイリアシングされたこのような信号を防ぐことができます。また、自動操縦のデジタルセクションのフィルターは補償器よりも高いサンプリングレートで動作し、調整された信号を補償器に提供します。信号がいったんエイリアシングされると、エイリアシングされた成分から有効なインバンド周波数成分を分離することはできないため、アナログフィルターは必要です。

この新しいコントローラーは Digital Control と呼ばれます。これらのフィルターのサンプル時間は deltat1 です (deltat の 1/10 に設定されています)。ゼロ次ホールドブロックでは、サンプル時間の継承により、これらのサンプル時間がさまざまな下流ブロックに対して指定されます。

slexAircraftPitchControlExample モデルのスイッチは、3 つの自動操縦、つまりアナログ自動操縦、デジタル LTI オブジェクト、ソフトウェアを使用して実装可能なデジタル自動操縦の間で切り替えることができるように設定されています。

このシステムを再びシミュレートし、これら 3 つの自動操縦設計間で切り替えてみます。どの自動操縦がアクティブであるかによって設計が大きな影響を受けることはないとわかるはずです。突風の振幅を大きくし、アンチエイリアシングフィルターが十分に機能しているかどうかを検証することもできます。突風の振幅を大きくするには、Dryden Wind Gust サブシステムを開き、突風シミュレーションを駆動するホワイトノイズのノイズ分散を変更します (アイコンをダブルクリック)。

DigitalControl サブシステムを開きます。

図 7: DigitalControl サブシステム

バリアントシステムによる設計のバリエーション

Simulink モデルのアクチュエータは Variant Subsystem ブロックを使って複数のアクチュエータ実装を表現します。ここで、シミュレーション中のアクティブな実装は 1 つだけとします。Variant Actuator Subsystem ブロックをダブルクリックすると、複数のアクチュエータ実装を表示できます。

シミュレーションを変更するには、線形アクチュエータではなく、非線形アクチュエータを使用します。Variant Subsystem ブロックの [バリアント]、[オーバーライドの方法] コンテキストメニューを使用することで、これを実行できます。

アクチュエータの選択を再設定するには、Simulink を停止しなければなりません。また、非線形アクチュエータでは位置と速度に飽和があります。

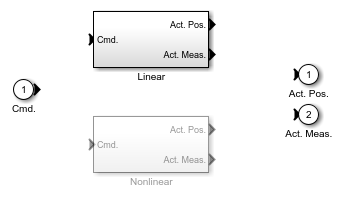
図 8: アクチュエータ用の Variant Subsystem

コード生成

Simulink Coder を使用して自動操縦設計を変換し、組み込み可能なコードにすることができます。デジタル自動操縦の別のモデル slexAircraftPitchControlDAP を以下で開いています。このモデルは Simulink Coder と mex -setup 設定で指定されたコンパイラを使用して、ホストベースのスタンドアロンプログラムにコーディングされています。シミュレーション結果は、生成コードが正しく機能するようにするための検証ベースラインとして使用できます。

コード生成とコンパイルの結果として得られる実行可能ファイルは slexAircraftPitchControlDAP.exe です。これを作成すると、OS シェル (DOS) コマンドラインから直接または MATLAB から実行できます。以下のとおり入力します。

>> !slexAircraftPitchControlDAP.exe

この実行可能プログラムは、slexAircraftPitchControlDAP.mat というファイルを生成します。このファイルは、load slexAircraftPitchControlDAP と入力して読み込むことができます。

2 つの変数 rt_tout および rt_yout がワークスペースに表示され、シミュレーションのベースラインに対する分散をプロットできます。ただし、このホスト上のこのモデルに関しては、分散は事実上ゼロです。これよりも計算が複雑な場合は、小さな数値分散が予想されます。これは、コンパイラの最適化の違いや、倍精度の 64 ビットストレージ形式よりも高精度な中間レジスタ変数の使用によるものです。分散が大きい場合は調べる必要があります。モデルのアルゴリズムの数値安定性や、コンパイラまたはランタイムライブラリのバグといった問題の表れである場合があるからです。

slexAircraftPitchControlDAP モデルを開きます。

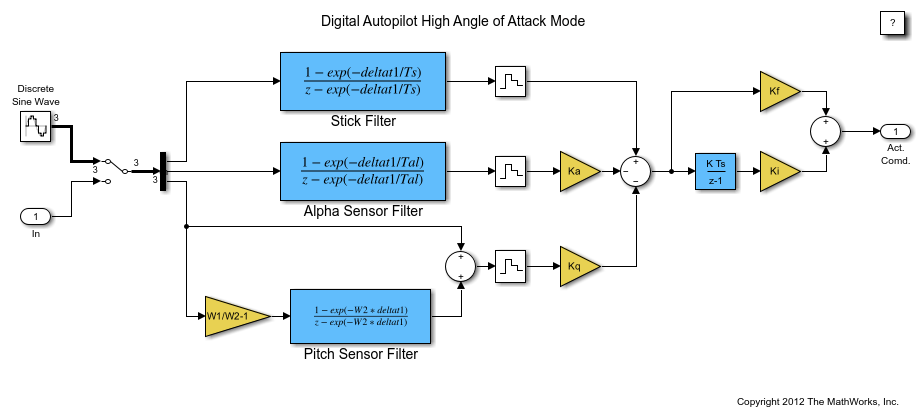
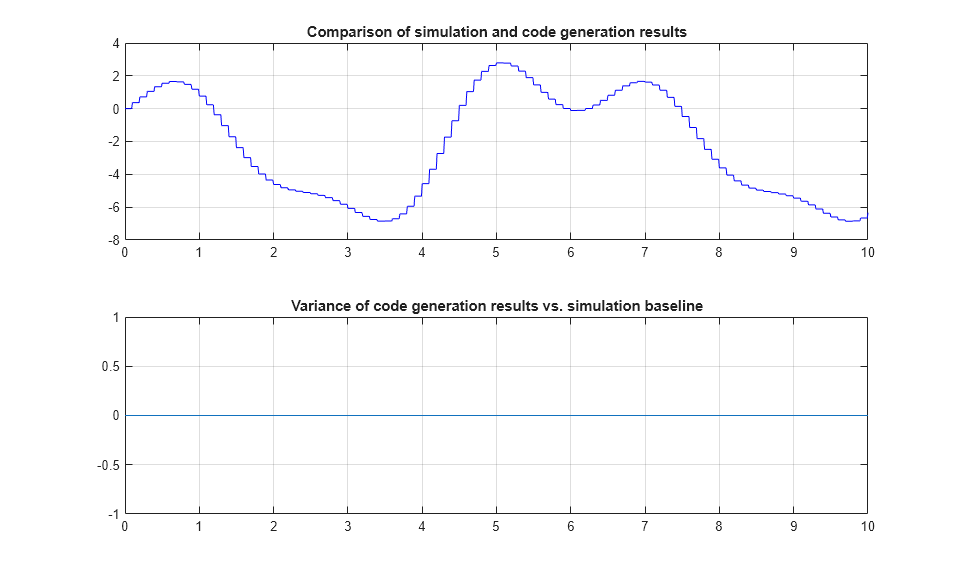
図 9: シミュレーション結果とコード生成結果の比較

第 1 段階の設計の動作

これは、高迎角攻撃モードのデジタルピッチコントローラー設計の時間応答です。

図 10: 航空機デジタルピッチ制御設計の応答

まとめ

この設計に対してさらに行う作業としては、たとえば、現実に補償器が受ける影響 (アンチエイリアシングフィルターのダイナミクスの効果や、デジタル計算による "プラント" 全体での組み込みデジタルコンピューターの計算遅延など) をより多く組み込み、解析することなどがあります。実際のプラント、計算遅延、アンチエイリアシングフィルター、サンプルアンドホールド遅延の組み合わせは、デジタル補償器パラメーターの設計に影響を与える可能性のある追加項目の一部にすぎません。

参考

linearize (Simulink Control Design) | Model Linearizer (Simulink Control Design)

高迎角のピッチ モード制御の設計