jointSpaceMotionModel
ジョイント空間の入力を与えて剛体ツリーの運動をモデル化
説明
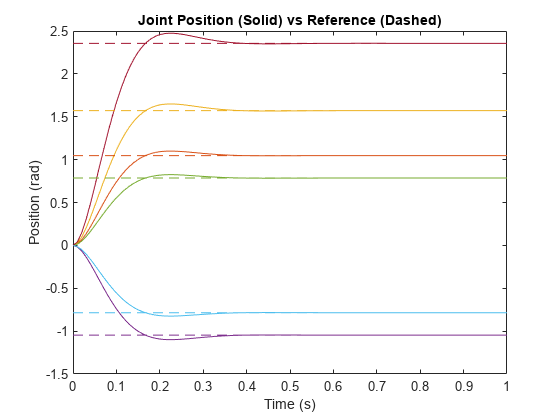
jointSpaceMotionModel オブジェクトは、rigidBodyTree オブジェクトとして指定されたマニピュレーター ロボットの閉ループのジョイント空間運動をモデル化します。運動モデルの動作は MotionType プロパティで定義されます。
運動方程式の詳細については、Joint-Space Motion Modelを参照してください。
作成
構文
説明
motionModel = jointSpaceMotionModel
motionModel = jointSpaceMotionModel("RigidBodyTree",tree)rigidBodyTree オブジェクトの運動モデルを作成します。
motionModel = jointSpaceMotionModel(Name,Value)
プロパティ
オブジェクト関数
derivative | Time derivative of manipulator model states |
updateErrorDynamicsFromStep | Update values of NaturalFrequency and
DampingRatio properties given desired step response |
例
この例では、マニピュレーター ロボットの jointSpaceMotionModel オブジェクトを作成してジョイント空間で使用する方法を示します。
ロボットの作成
robot = loadrobot("kinovaGen3",DataFormat="column",Gravity=[0 0 -9.81]);
シミュレーションの設定
時間範囲を 0.01 秒のタイム ステップ サイズで 1 秒に設定します。初期状態をロボットの速度ゼロのホーム コンフィギュレーションに設定します。
tspan = 0:0.01:1; initialState = [homeConfiguration(robot); zeros(7,1)];
基準状態をターゲット位置、ゼロ速度、ゼロ加速度で定義します。
targetState = [pi/4; pi/3; pi/2; -pi/3; pi/4; -pi/4; 3*pi/4; zeros(7,1); zeros(7,1)];
運動モデルの作成
5% のオーバーシュートをもつ適度な速さのステップ応答で定義される計算トルク制御と誤差ダイナミクスを使用してシステムをモデル化します。
motionModel = jointSpaceMotionModel(RigidBodyTree=robot); updateErrorDynamicsFromStep(motionModel,0.3,0.05);
ロボットのシミュレーション
モデルの導関数をode45ソルバーへの入力として使用して 1 秒間の動作をシミュレートします。
[t,robotState] = ode45(@(t,state)derivative(motionModel,state,targetState),tspan,initialState);
応答のプロット
すべてのジョイントについて、ターゲットの状態まで作動する位置をプロットします。開始位置からターゲット位置までの変位が大きいジョイントの方が、変位が小さいものよりも速いレートでターゲットまで作動します。これによってオーバーシュートが発生しますが、すべてのジョイントの整定時間が同じになります。
figure plot(t,robotState(:,1:motionModel.NumJoints)); hold on plot(t,targetState(1:motionModel.NumJoints)*ones(1,length(t)),"--"); title("Joint Position (Solid) vs Reference (Dashed)"); xlabel("Time (s)") ylabel("Position (rad)"); hold off
参照
[1] Craig, John J. Introduction to Robotics: Mechanics and Control. Upper Saddle River, NJ: Pearson Education, 2005.
[2] Spong, Mark W., Seth Hutchinson, and Mathukumalli Vidyasagar. Robot Modeling and Control. Hoboken, NJ: Wiley, 2006.
