ギア列故障検出のためのモーター電流シグネチャ解析
この例では、ホビーグレードのサーボを駆動する電流信号にモーター電流シグネチャ解析 (MCSA) を使用して、ギア列の故障を発見する方法を説明します。MCSA はトルクまたは速度の変動を誘発する故障を診断するのに役立つ手法であり、モーターの故障解析に最適な方法であることが実証されています。特に、原子力発電所の内部機構などのように、加速度計またはその他の振動センサーでアクセスして計測するのが容易ではない場合、従来の振動計を使用したギア故障検出は困難です。この例では、電流シグネチャ解析を適用してスペクトル メトリクスを抽出し、ホビーグレードのサーボ モーターの駆動ギアの故障を検出する方法を説明します。電流信号からスペクトル メトリクスを取得するワークフローは、簡略化すると以下のとおりです。
定格 rpm を計算して対象とする周波数を検出する。
故障信号が存在する可能性のある周波数帯域を構築する。
パワー スペクトル密度 (PSD) データを抽出する。
対象の周波数帯域のスペクトル メトリクスを計算する。
ハードウェアの概要

この例では、Futaba の標準的なホビー用サーボ S3003 を連続回転用に改造したものから電流データを収集しました。サーボは、内部の DC モーターの高い速度を、出力スプラインの高いトルクに変換します。これを可能にするため、サーボは DC モーター、ナイロン製または金属製駆動ギアの組、および制御回路によって構成されます。制御回路は、DC モーターへの電流信号を直接監視するため取り外しました。サーボの出力スプラインのタコメーター信号を収集するため、直径 35 mm、8 穴の標準的なホビー用サーボ ホイールともに赤外線フォトインタラプタを使用しました。ホイールの 8 つの穴は等間隔です。IR フォトインタラプタはサーボ ホイールのホーン 1 回転に付き正確に 8 パルスになるよう配置しました。サーボとフォトインタラプタは、カスタムで 3 次元プリントしたマウントによって保持しました。

DC モーターは 5 V の定電圧で駆動され、4 組のギアで 278:1 の減速を行うため、スプラインのシャフト速度は約 50 rpm になります。消費電流は、0.5 Ω の抵抗の両端の電圧低下を測定することによってオームの法則を使用して計算されました。電流測定値の変化は小さすぎて検出できないため、単電源センサー インターフェイス アンプを使用して電流信号を増幅しました。増幅された電流信号は、アンチエイリアシング 5 次楕円ローパス フィルターを使用して平滑化とノイズ除去を行ってから、アナログ デジタル コンバーター (ADC) を介して Arduino® Uno に送られました。

フロー チャートに示すように、電流信号はまずアンプで増幅されてから、アンチエイリアシング ローパス フィルターでフィルター処理されます。Arduino Uno は、ADC を通して送られた電流信号を 1.5 kHz でサンプリングし、タコメーターのパルスとともにシリアル データとして 115200 のボー レートでコンピューターにストリーミングします。MATLAB® スクリプトが Arduino Uno からシリアル データを取得し、コンマ区切り値 (CSV) ファイルに書き込みます。その後、MATLAB を使用してその CSV ファイルを読み込み、スペクトル メトリクスを抽出します。
サーボのギア列
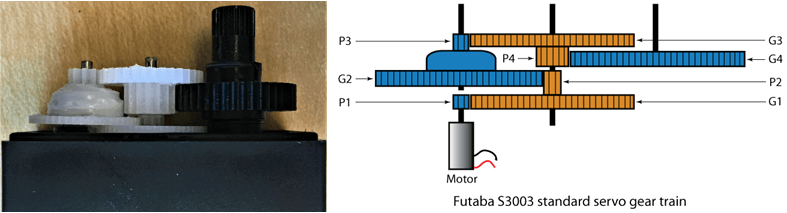
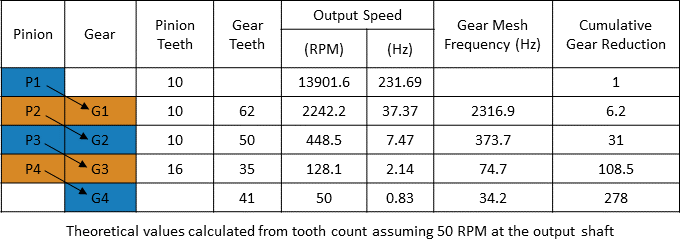
上図に示すように、Futaba の S3003 サーボは、4 組のナイロン製ギアで構成されています。DC モーター シャフト上のピニオン P1 は段付きギア G1 と噛み合います。ピニオン P2 は段付きギア G1 の成形部分であり、段付きギア G2 と噛み合います。ピニオン P3 はギア G2 の成形部分であり、段付きギア G3 と噛み合います。ピニオン P4 は G3 の成形部分であり、出力スプラインに取り付けられた最終ギア G4 と噛み合います。G1 と P2、G2 と P3、G3 と P4 の段付きギアの組は自由回転ギアです すなわち、これらは各シャフトに固定されていません。駆動ギアの組は 278:1 の減速を行い、モーターを 5 V で駆動するとき、13901 rpm のモーター速度を約 50 rpm の出力スプラインに減速します。次の表に、歯数と、各ギア噛み合いにおける出力速度、ギアの噛み合い周波数、累積ギア減速比の理論値を示します。
合計 10 個の健全なデータセットを収集した後、段付きギア G2 および G3 に故障を発生させました。ギアはナイロン成形品のため、両ギアの歯溝にホビー ナイフで切れ込みを入れることにより、擬似的なクラックを発生させました。歯溝とは隣り合う 2 つの歯の間を指し、平ギアのピッチ円に沿って計測されます。切れ込みの深さは、ギアの半径の約 70% にしました。ギア G2 および G3 に故障を発生させた後、合計 10 個の故障データセットを記録しました。

データの可視化
ファイル mcsaData.mat には、10 行 2 列の timetable の table である servoData が含まれます。各 timetable が 1 つのデータセットに対応します。servoData の 1 列目には健全なデータの 10 個の timetable が含まれ、2 列目には故障データの 10 個の timetable が含まれます。各データセットには、1500 Hz でサンプリングされた約 11 秒のデータが含まれます。
データを読み込みます。
load('mcsaData.mat','servoData') servoData
servoData=10×2 table
healthyData faultyData
___________________ ___________________
{16384×2 timetable} {16384×2 timetable}
{16384×2 timetable} {16384×2 timetable}
{16384×2 timetable} {16384×2 timetable}
{16384×2 timetable} {16384×2 timetable}
{16384×2 timetable} {16384×2 timetable}
{16384×2 timetable} {16384×2 timetable}
{16384×2 timetable} {16384×2 timetable}
{16384×2 timetable} {16384×2 timetable}
{16384×2 timetable} {16384×2 timetable}
{16384×2 timetable} {16384×2 timetable}
head(servoData.healthyData{1,1}) Time Pulse Signal
______________ _____ ______
0 sec 0 66.523
0.00066667 sec 0 62.798
0.0013333 sec 0 63.596
0.002 sec 0 64.128
0.0026667 sec 0 60.669
0.0033333 sec 0 62.798
0.004 sec 0 65.459
0.0046667 sec 0 56.678
servoData の各 timetable には、1 列目にタコメーター信号、2 列目に電流信号を含む 1 つのデータセットが含まれます。
この例では、健全データと故障データのそれぞれについて 1 つのセットを考え、電流信号とタコメーター パルスを可視化します。
healthyData = servoData.healthyData{1,1};
faultyData = servoData.faultyData{1,1};
healthyCurrent = healthyData.Signal;
faultyCurrent = faultyData.Signal;
healthyTacho = healthyData.Pulse;
faultyTacho = faultyData.Pulse;
tHealthy = healthyData.Time;
tFaulty = faultyData.Time;
figure
ax1 = subplot(221);
plot(tHealthy,healthyCurrent)
title('Current Signal - Healthy Gears')
ylabel('Current (mA)')
ax2 = subplot(222);
plot(tFaulty,faultyCurrent)
title('Current Signal - Faulty Gears')
ylabel('Current (mA)')
ax3 = subplot(223);
plot(tHealthy,healthyTacho)
title('Tachometer Pulse - Healthy Gears')
ylabel('Pulses, 8/rev')
ax4 = subplot(224);
plot(tFaulty,faultyTacho)
title('Tachometer Pulse - Faulty Gears')
ylabel('Pulses, 8/rev')
linkaxes([ax1,ax2,ax3,ax4],'x');
ax1.XLim = seconds([0 2]);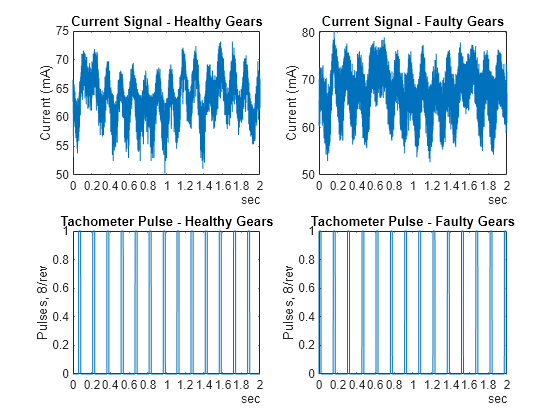
サーボの出力スプラインは、1 回転につき、サーボ ホイールの 8 つの穴に対応する 8 つのパルスをもっています。
定格 rpm の計算
定格速度を計算してギアシステムの対象の周波数を検出し、パワー スペクトル上の周波数と正しく照合します。1500 Hz のサンプリング周波数値を使用してタコメーター信号を可視化し、tachorpmを使用して定格 rpm を計算します。
fs = 1500;
figure
tachorpm(healthyTacho,fs,'PulsesPerRev',8)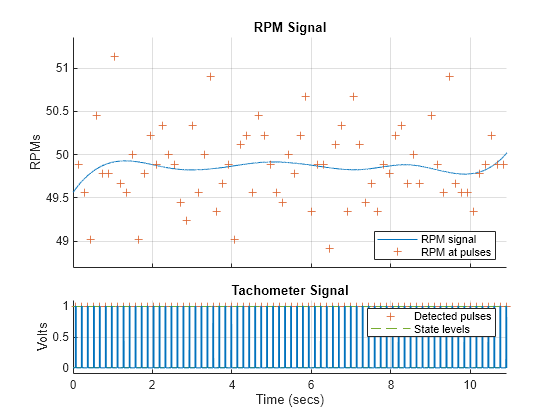
figure
tachorpm(faultyTacho,fs,'PulsesPerRev',8)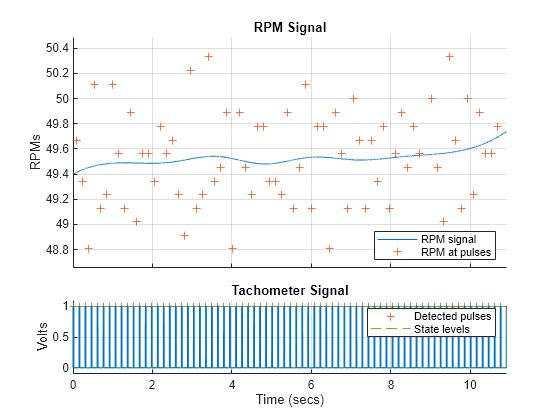
rpmHealthy = mean(tachorpm(healthyTacho,fs,'PulsesPerRev',8))rpmHealthy = 49.8550
rpmFaulty = mean(tachorpm(faultyTacho,fs,'PulsesPerRev',8))rpmFaulty = 49.5267
健全データセットと故障データセットの間で、出力シャフト速度にごくわずかな違いがあることを確認します。また、実際の定格 rpm 値は、理論値の 50 rpm に近くなっています。そのため、健全信号解析と故障信号解析の両方に 49.9 rpm という同じ値を考えます。
周波数帯域の構築
周波数帯域の構築は、スペクトル メトリクスを計算するための重要な前提条件です。まず、ギア列の駆動ギアの歯数と定格 rpm を使用して、対象周波数を計算します。対象周波数は実際の出力速度の値 (Hz 単位) で、次の表に示す理論値に近い値になります。

G4 = 41; G3 = 35; G2 = 50; G1 = 62; P4 = 16; P3 = 10; P2 = 10; P1 = 10; rpm = rpmHealthy; FS5 = mean(rpm)/60; FS4 = G4/P4*FS5; FS3 = G3/P3*FS4; FS2 = G2/P2*FS3; FS1 = G1/P1*FS2; FS = [FS1,FS2,FS3,FS4,FS5]
FS = 1×5
231.0207 37.2614 7.4523 2.1292 0.8309
次に、faultBandsを使用して、次の対象周波数を含むすべての出力速度に対する周波数帯域を構築します。
FS1 (231 Hz)、その最初の 2 つの高調波、および FS2 の 0:1 側波帯
FS2 (37.3 Hz)、その最初の 2 つの高調波、および FS3 の 0:1 側波帯
FS3 (7.5 Hz) およびその最初の 2 つの高調波
FS4 (2.1 Hz) およびその最初の 2 つの高調波
[FB1,info1] = faultBands(FS1,1:2,FS2,0:1); [FB2,info2] = faultBands(FS2,1:2,FS3,0:1); [FB3,info3] = faultBands(FS3,1:2); [FB4,info4] = faultBands(FS4,1:2); FB = [FB1;FB2;FB3;FB4]
FB = 16×2
187.9838 199.5348
225.2452 236.7962
262.5066 274.0577
419.0045 430.5556
456.2659 467.8170
493.5273 505.0784
28.8776 30.7407
36.3299 38.1929
43.7822 45.6452
66.1390 68.0021
73.5913 75.4543
81.0436 82.9066
7.2660 7.6386
14.7183 15.0909
2.0760 2.1825
⋮
出力 FB は、これらの対象周波数に対する周波数範囲の 16 行 2 列の配列です。
パワー スペクトル密度 (PSD) データの抽出
健全データと故障データのパワー スペクトルを計算し、可視化します。また、構造体 info の情報を使用して、対象周波数をスペクトル プロット上にプロットします。
figure pspectrum(healthyCurrent,fs,'FrequencyResolution',0.5) hold on pspectrum(faultyCurrent,fs,'FrequencyResolution',0.5) hold on info1.Labels = regexprep(info1.Labels,'F0','FS1'); info1.Labels = regexprep(info1.Labels,'F1','FS2'); helperPlotXLines(info1,[0.5 0.5 0.5]) info2.Labels = regexprep(info2.Labels,'F0','FS2'); info2.Labels = regexprep(info2.Labels,'F1','FS3'); helperPlotXLines(info2,[0.5 0.5 0.5]) info3.Labels = regexprep(info3.Labels,'F0','FS3'); helperPlotXLines(info3,[0.5 0.5 0.5]) info4.Labels = regexprep(info4.Labels,'F0','FS4'); helperPlotXLines(info4,[0.5 0.5 0.5]) legend('Healthy Data','Faulty Data','Location','South') hold off
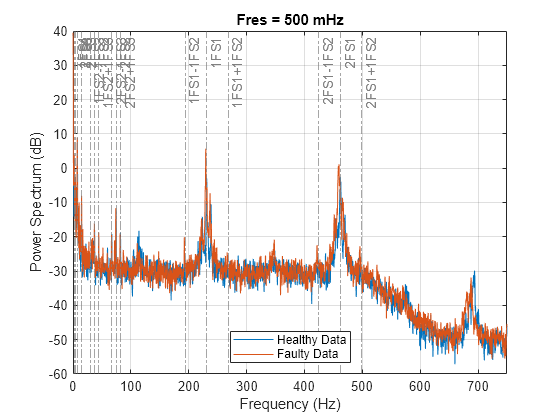
青色のプロットは健全なスペクトルを表し、赤色のプロットは故障データのスペクトルを表しています。このプロットから、以下の故障周波数において振幅が増加していることを確認します。
1FS1 (231 Hz)、その第 2 高調波である 2FS1 (462 Hz)、およびそれぞれの側波帯
プロットを拡大表示して、次の残りの周波数における振幅の増加を確認します。
1FS2 (37.2 Hz) およびその側波帯
1FS3 (7.5 Hz) およびそのその第 2 高調波である 2FS3 (15 Hz)
1FS4 (2.1 Hz) およびそのその第 2 高調波である 2FS4 (4.2 Hz)
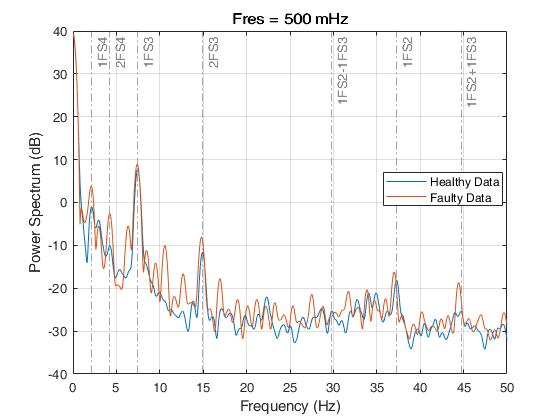
pspectrumを使用して、健全信号と故障信号それぞれの PSD と周波数グリッド データを計算し、保存します。
[psdHealthy,fHealthy] = pspectrum(healthyCurrent,fs,'FrequencyResolution',0.5); [psdFaulty,fFaulty] = pspectrum(faultyCurrent,fs,'FrequencyResolution',0.5);
スペクトル メトリクスの計算
周波数帯域および PSD データから、faultBandMetricsを使用して、健全データと故障データのスペクトル メトリクスを計算します。
spectralMetrics = faultBandMetrics({[psdHealthy,fHealthy],[psdFaulty,fFaulty]},FB)spectralMetrics=2×49 table
PeakAmplitude1 PeakFrequency1 BandPower1 PeakAmplitude2 PeakFrequency2 BandPower2 PeakAmplitude3 PeakFrequency3 BandPower3 PeakAmplitude4 PeakFrequency4 BandPower4 PeakAmplitude5 PeakFrequency5 BandPower5 PeakAmplitude6 PeakFrequency6 BandPower6 PeakAmplitude7 PeakFrequency7 BandPower7 PeakAmplitude8 PeakFrequency8 BandPower8 PeakAmplitude9 PeakFrequency9 BandPower9 PeakAmplitude10 PeakFrequency10 BandPower10 PeakAmplitude11 PeakFrequency11 BandPower11 PeakAmplitude12 PeakFrequency12 BandPower12 PeakAmplitude13 PeakFrequency13 BandPower13 PeakAmplitude14 PeakFrequency14 BandPower14 PeakAmplitude15 PeakFrequency15 BandPower15 PeakAmplitude16 PeakFrequency16 BandPower16 TotalBandPower
______________ ______________ __________ ______________ ______________ __________ ______________ ______________ __________ ______________ ______________ __________ ______________ ______________ __________ ______________ ______________ __________ ______________ ______________ __________ ______________ ______________ __________ ______________ ______________ __________ _______________ _______________ ___________ _______________ _______________ ___________ _______________ _______________ ___________ _______________ _______________ ___________ _______________ _______________ ___________ _______________ _______________ ___________ _______________ _______________ ___________ ______________
0.0020712 193.75 0.010881 0.50813 231.06 0.46652 0.0019579 272.5 0.011841 0.0020486 424.06 0.011225 0.54982 462 0.89544 0.0024293 493.69 0.0091045 0.002966 29.812 0.0035485 0.015582 37.25 0.011132 0.0028865 44.688 0.0041317 0.011896 67.062 0.0072753 0.059126 74.5 0.033568 0.013218 82 0.0079886 5.7904 7.4375 2.3115 0.068452 14.938 0.027653 0.79006 2.125 0.14382 0.09849 4.25 0.01806 3.9737
0.009804 192.44 0.017916 3.6921 229.44 2.9975 0.0035204 266.44 0.015639 0.0057056 421.75 0.019293 1.2974 459.69 3.2185 0.0053261 495.88 0.016296 0.0031674 28.938 0.0044271 0.023983 37 0.014447 0.0136 44.438 0.0089119 0.011419 66.625 0.0077035 0.0684 74 0.037016 0.012244 81.438 0.0075805 7.7931 7.375 3.0193 0.15692 14.812 0.058255 2.4211 2.125 0.4407 0.55167 4.25 0.10029 9.9838
出力は FB の周波数範囲に対するメトリクスの 2 行 49 列の table になります。1 行目には健全データのメトリクスが、2 行目には故障データのメトリクスが含まれます。次のメトリクスについて、故障データの方が健全データよりも大幅に高い値をもつことを確認します。
PeakAmplitude2。周波数 231 Hz での差が 3.1842 単位あるTotalBandPower。6.01 単位の差がある
そのため、これらの 2 つのメトリクスを使用して、散布図を作成し、故障データセットと健全データセットを別々にグループ化します。
散布図の作成
散布図を作成し、table servoData 内の全 20 のデータセットについて、2 つのスペクトル メトリクス PeakAmplitude2 および TotalBandPower を使用して、健全データと故障データを分類します。
plotData = zeros(10,4); for n = 1:max(size(servoData)) hC = servoData.healthyData{n,1}.Signal; fC = servoData.faultyData{n,1}.Signal; [psdH,freqH] = pspectrum(hC,fs,'FrequencyResolution',0.5); [psdF,freqF] = pspectrum(fC,fs,'FrequencyResolution',0.5); sMetrics = faultBandMetrics({[psdH,freqH],[psdF,freqF]},FB); plotData(n,:) = [sMetrics{:,4}',sMetrics{:,49}']; end figure scatter(plotData(:,1),plotData(:,3),[],'blue') hold on; scatter(plotData(:,2),plotData(:,4),[],'red') legend('Healthy Data','Faulty Data','Location','best') xlabel('Peak Amplitude 2') ylabel('Total Band Power') hold off
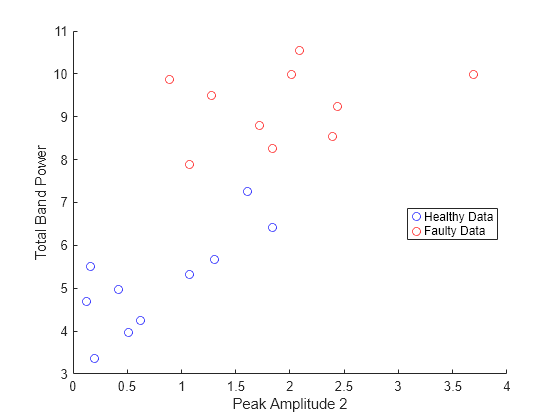
健全データセットと故障データセットが散布図の異なる領域にグループ化されるのを確認します。
したがって、サーボ モーターの電流シグネチャを解析することで、故障データと健全データを分類することができます。
分類に利用可能なすべてのスペクトル メトリクスを使用するには、分類学習器を使用します。
補助関数
補助関数 helperPlotXLines は、構造体 info の情報を使用して、パワー スペクトル プロット上に周波数帯域の中央線をプロットします。
function helperPlotXLines(I,c) for k = 1:length(I.Centers) xline(I.Centers(k),'Label',I.Labels(k),'LineStyle','-.','Color',c); end end
参照
[1] Moster, P.C. "Gear Fault Detection and Classification Using Learning Machines." Sound & vibration. 38. 22-27. 2004