phased.IsotropicHydrophone
Isotropic hydrophone element
Description
The phased.IsotropicHydrophone
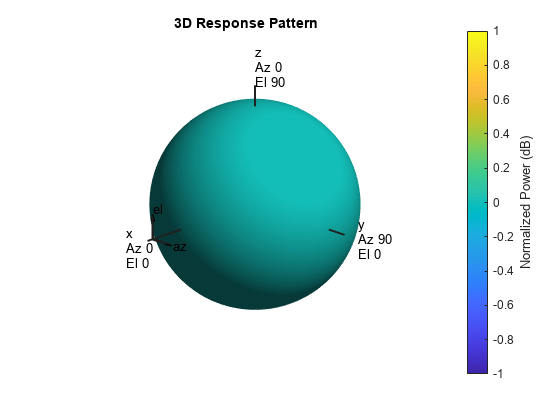
System object™ models an isotropic hydrophone for sonar applications. An isotropic
hydrophone has the same response in all signal directions. The response is the output
voltage of the hydrophone per unit sound pressure. The response of a hydrophone is also
called its sensitivity. You can specify the response using the
VoltageSensitivity property.
To compute the response of the isotropic hydrophone element for specified directions:
Create the
phased.IsotropicHydrophoneobject and set its properties.Call the object with arguments, as if it were a function.
To learn more about how System objects work, see What Are System Objects?
Creation
Description
hydrophone = phased.IsotropicHydrophonehydrophone.
hydrophone = phased.IsotropicHydrophone(Name=Value)hydrophone, with
each specified property set to the specified value. You can specify additional
name-value pair arguments in any order as
(Name1=Value1,...,NameN=ValueN).
Example: hydrophone = phased.IsotropicHydrophone(FrequencyRange=[0
1000],BackBaffled=true) creates an isotropic hydrophone element
with its frequency range specified between 0 and 1000 Hz.
Properties
Usage
Description
Input Arguments
Output Arguments
Object Functions
To use an object function, specify the
System object as the first input argument. For
example, to release system resources of a System object named obj, use
this syntax:
release(obj)
Examples
More About
Algorithms
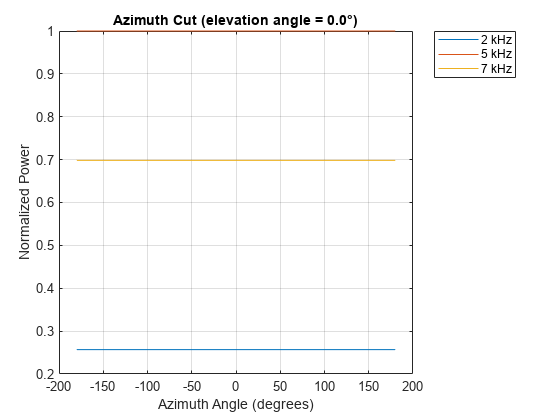
The total sensitivity of a hydrophone is a combination of its frequency sensitivity
and spatial sensitivity. phased.IsotropicHydrophone
calculates both sensitivities using nearest neighbor interpolation, and then multiplies
the sensitivities to form the total sensitivity.
References
[1] Urick, R.J. Principles of Underwater Sound. 3rd Edition. New York: Peninsula Publishing, 1996.
[2] Sherman, C.S., and J. Butler. Transducers and Arrays for Underwater Sound. New York: Springer, 2007.
[3] Allen, J.B., and D. Berkely. “Image method for efficiently simulating small-room acoustics”, Journal of the Acoustical Society of America. Vol. 65, No. 4. April 1979, pp. 943–950.
[4] Van Trees, H. Optimum Array Processing. New York: Wiley-Interscience, 2002, pp. 274–304.
Extended Capabilities
Version History
Introduced in R2017a