パラメーターの変化に応じた方程式の解の追跡

この例では、パラメーターが変化したときに、前回の解の点から後続の求解を始めることで、方程式を繰り返し解く方法を示します。多くの場合、このプロセスで効率的に解を求めることができます。ただし、解が見つからないこともあり、その場合は新しい点から開始する必要があります。

パラメーター付きスカラー方程式

これから解くパラメーター付き方程式は次のとおりです。

$$\sinh (x)-3x=a$$,

ここで、$$a$$ は 0 ～ 5 の数値パラメーターです。$$a=0$$ の場合、この方程式の解の 1 つは $$x=0$$ です。$$a$$ の絶対値が大きすぎない場合、この方程式には 3 つの解があります。方程式を視覚化するために、方程式の左辺を無名関数として作成します。関数をプロットします。

fun = @(x)sinh(x) - 3*x;
t = linspace(-3.5,3.5);
plot(t,fun(t),t,zeros(size(t)),'k-')
xlabel('x')
ylabel('fun(x)')

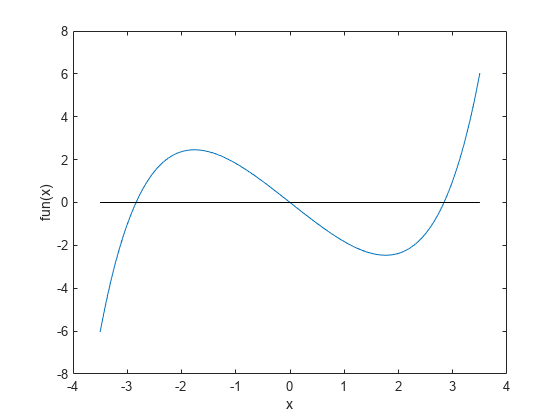
$$a$$ が大きすぎるか小さすぎる場合、解は 1 つのみになります。

問題ベースの設定

問題ベースのアプローチで目的関数を作成するには、最適化変数 x の最適化式 expr を作成します。

x = optimvar('x');
expr = sinh(x) - 3*x;

解の作成とプロット

$$a=0$$ での初期解 $$x=0$$ から開始して、$$a$$ が 0 から 5 までの 100 個の値での解を求めます。fun はスカラー非線形関数であるため、solve はソルバーとして fzero を呼び出します。

問題オブジェクト、オプション、解の統計量を保持するためのデータ構造体を設定します。

prob = eqnproblem;
options = optimset('Display','off');
sols = zeros(100,1);
fevals = sols;
as = linspace(0,5);

最初の解 sols(1) = 0 から開始して、ループで方程式を解きます。

for i = 2:length(as)
    x0.x = sols(i-1); % Start from previous solution
    prob.Equations = expr == as(i);
    [sol,~,~,output] = solve(prob,x0,'Options',options);
    sols(i) = sol.x;
    fevals(i) = output.funcCount;
end

パラメーター a の関数として解をプロットし、解に到達するまでに行った関数評価の回数もプロットします。

subplot(2,1,1)
plot(as,sols,'ko')
xlabel 'a'
ylabel('Solution(x)')
subplot(2,1,2)
plot(fevals,'k*')
xlabel('Iteration Number')
ylabel('Fevals')

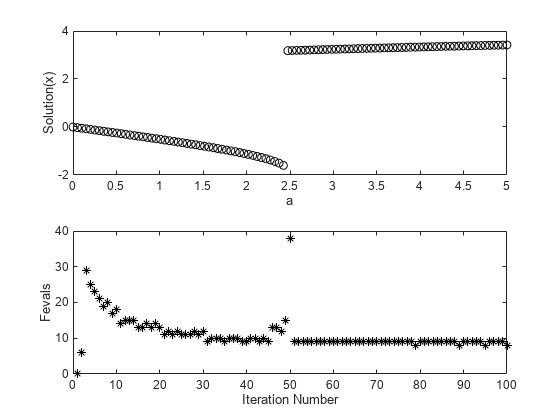
$$a=2.5$$ 付近で解が急に変化します。同じ点で、解に到達するまでの関数評価の回数が 15 付近から 40 付近に増加します。理由を理解するために、関数のより詳細なプロットを確認します。関数とともに、解の点を 7 つごとにプロットします。

figure
t = linspace(-3.5,3.5);
plot(t,fun(t));
hold on
plot([-3.5,min(sols)],[2.5,2.5],'k--')
legend('fun','Maximum a','Location','north','autoupdate','off')
for a0 = 7:7:100
    plot(sols(a0),as(a0),'ro')
    if mod(a0,2) == 1
        text(sols(a0) + 0.15,as(a0) + 0.15,num2str(a0/7))
    else
        text(sols(a0) - 0.3,as(a0) + 0.05,num2str(a0/7))
    end
end
plot(t,zeros(size(t)),'k-')
hold off

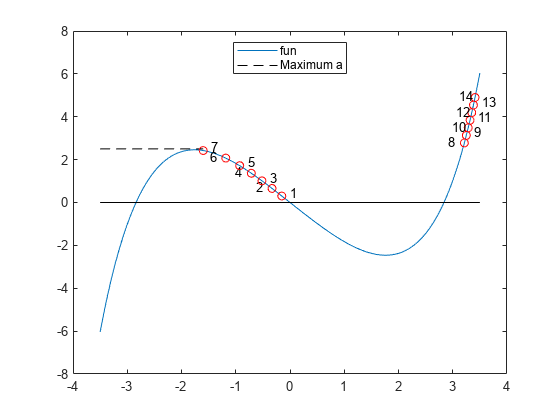
$$a$$ が増加すると、最初は解が左へ動いていきます。しかし、$$a$$ が 2.5 を超えると、前回の解に近い解はなくなります。fzero では、解を探索して x = 3 付近の解を求めるために、追加の関数評価が必要になります。その後、$$a$$ がさらに増加するにつれて、解の値は徐々に右へ動いていきます。それ以降の解についてはそれぞれ、ソルバーで必要な関数評価は約 10 回だけです。

別のソルバーの選択

fsolve ソルバーは、fzero よりも効率的な場合があります。ただし fsolve は、局所的最小値に陥ったり、方程式が解けなかったりすることもあります。

問題オブジェクト、オプション、解の統計量を保持するためのデータ構造体を設定します。

probfsolve = eqnproblem;
sols = zeros(100,1);
fevals = sols;
infeas = sols;
asfsolve = linspace(0,5);

最初の解 sols(1) = 0 から開始して、ループで方程式を解きます。

for i = 2:length(as)
    x0.x = sols(i-1); % Start from previous solution
    probfsolve.Equations = expr == asfsolve(i);
    [sol,fval,~,output] = solve(probfsolve,x0,'Options',options,'Solver','fsolve');
    sols(i) = sol.x;
    fevals(i) = output.funcCount;
    infeas(i) = fval;
end

パラメーター a の関数として解をプロットし、解に到達するまでに行った関数評価の回数もプロットします。

subplot(2,1,1)
plot(asfsolve,sols,'ko',asfsolve,infeas,'r-')
xlabel 'a'
legend('Solution','Error of Solution','Location','best')
subplot(2,1,2)
plot(fevals,'k*')
xlabel('Iteration Number')
ylabel('Fevals')

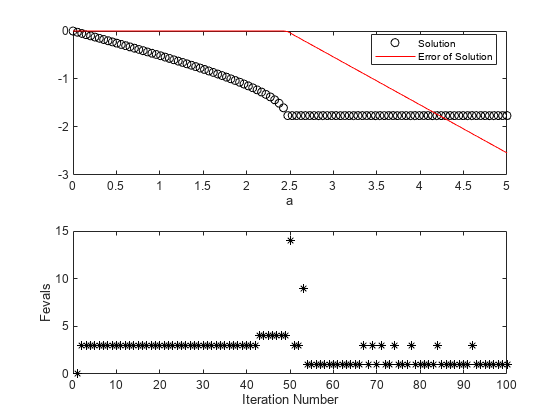
fsolve は fzero よりも多少効率的であり、必要な関数評価は反復ごとに約 7 ～ 8 回です。この場合も、ソルバーが前回の値の付近で解を見つけられないと、解を探索するために必要な関数評価の回数が増えます。今回は探索に失敗しています。以降の反復では、必要な関数評価の回数は概ね減っていますが、解を見つけることができていません。Error of Solution のプロットは、関数値 $$fun(x)-a$$ を示しています。

局所的最小値が解にならない状況に対処するには、fsolve が負の終了フラグを返した場合に、別の開始点から探索を再度行います。問題オブジェクト、オプション、解の統計量を保持するためのデータ構造体を設定します。

rng default % For reproducibility
sols = zeros(100,1);
fevals = sols;
asfsolve = linspace(0,5);

最初の解 sols(1) = 0 から開始して、ループで方程式を解きます。

for i = 2:length(as)
    x0.x = sols(i-1); % Start from previous solution
    probfsolve.Equations = expr == asfsolve(i);
    [sol,~,exitflag,output] = solve(probfsolve,x0,'Options',options,'Solver','fsolve');
    
    while exitflag <= 0 % If fsolve fails to find a solution
        x0.x = 5*randn; % Try again from a new start point
        fevals(i) = fevals(i) + output.funcCount;
        [sol,~,exitflag,output] = solve(probfsolve,x0,'Options',options,'Solver','fsolve');
    end
    
    sols(i) = sol.x;
    fevals(i) = fevals(i) + output.funcCount;
end

パラメーター a の関数として解をプロットし、解に到達するまでに行った関数評価の回数もプロットします。

subplot(2,1,1)
plot(asfsolve,sols,'ko')
xlabel 'a'
ylabel('Solution(x)')
subplot(2,1,2)
plot(fevals,'k*')
xlabel('Iteration Number')
ylabel('Fevals')

今度は、fsolve が $$a=2.5$$ 付近の不適切な初期点から復帰し、fzero で取得した解とほぼ同じ解を取得しています。反復ごとの関数評価の回数はほとんどが 8 回であり、解が急に変化した点で約 30 回まで増加しています。

fcn2optimexpr を使用した目的関数の変換

一部の目的関数またはソフトウェア バージョンでは、fcn2optimexpr を使用して、非線形関数を最適化式に変換しなければなりません。詳細については、最適化変数および式でサポートされる演算と非線形関数から最適化式への変換を参照してください。この例では、次のように、プロットに使用される元の関数 fun を最適化式 expr に変換します。

expr = fcn2optimexpr(fun,x);

expr の定義を変更しましたが、この例の続く部分はまったく同じです。

参考

fzero | fsolve | solve

関連するトピック

• 非線形方程式系
• 方程式を解くための問題ベースのワークフロー