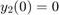ode23t

中程度にスティッフな常微分方程式 (ODE) と微分代数方程式 (DAE) の求解 — 台形則

構文

[t,y] = ode23t(odefun,tspan,y0)

[t,y] = ode23t(odefun,tspan,y0,options)

[t,y,te,ye,ie] = ode23t(odefun,tspan,y0,options)

sol = ode23t(___)

説明

[t,y] = ode23t(odefun,tspan,y0) は、tspan = [t0 tf] のときに、初期条件 y0 を使用して、連立微分方程式 $y' = f (t, y)$ を t0 から tf まで積分します。解の配列 y の各行は、列ベクトル t に返される値に対応します。

すべての MATLAB^® ODE ソルバーは、 $y' = f (t, y)$ の形式の連立方程式、あるいは質量行列 $M (t, y) y' = f (t, y)$ を含む問題を解くことができます。すべてのソルバーは類似した構文を使用します。ode23s ソルバーは、質量行列が定数である場合にのみ、これを含む問題を解くことができます。ode15s および ode23t は、特異質量行列をもつ方程式、つまり微分代数方程式 (DAE) を解くことができます。odeset の Mass オプションを使用して質量行列を指定します。

例

[t,y] = ode23t(odefun,tspan,y0,options) は options (関数 odeset を使用して作成された引数) で定義された積分設定も使用します。たとえば、AbsTol オプションおよび RelTol オプションを使用して絶対許容誤差と相対許容誤差を指定したり、Mass オプションを使用して質量行列を指定することができます。

例

[t,y,te,ye,ie] = ode23t(odefun,tspan,y0,options) はさらに、(t,y) の関数 (イベント関数) がゼロになる点を求めます。出力の te はイベント時点、ye はイベント時点における解、ie はトリガーされたイベントのインデックスです。

各関数に対して、ゼロで積分を終了するかどうかと、ゼロクロッシングの方向を考慮するかどうかを指定します。これを行うには、myEventFcn や @myEventFcn などの関数に 'Events' プロパティを設定し、対応する関数 [value,isterminal,direction] = myEventFcn(t,y) を作成します。詳細については、ODE のイベント検出を参照してください。

sol = ode23t(___) は、区間 [t0 tf] の任意の点で解を計算する関数 deval で使用できる構造体を返します。前述の構文にある任意の入力引数の組み合わせが使用できます。

例

すべて折りたたむ

単一解要素をもつ ODE

ライブスクリプトを開く

単一解要素をもつシンプルな ODE は、ソルバーの呼び出し内に無名関数として指定できます。この無名関数は、2 つの入力 (t,y) を受け入れなければなりません (いずれかの入力が関数で使用されない場合でも)。

次の ODE を解きます。

$y^{'} = - 10 t .$

時間区間 [0 2] および初期条件 y0 = 1 を指定します。

tspan = [0 2];
y0 = 1;
[t,y] = ode23t(@(t,y) -10*t, tspan, y0);

解をプロットします。

plot(t,y,'-o')

Figure contains an axes object. The axes object contains an object of type line.

スティッフな ODE の求解

スクリプトを開く

スティッフな連立方程式の例の 1 つに緩和振動に関するファンデルポールの方程式があります。このリミットサイクルには、解の成分がゆっくり変化して問題がかなりスティッフな領域と、急激に変化してスティッフでない領域が交互にあります。

連立方程式は次のとおりです。

$\begin{array}{cl} y_1' &= y_2\\y_2' &= 1000(1-y_1^2)y_2-y_1\end{array}$

初期条件は、 $y_1(0)=2$ および $y_2(0)=0$ です。MATLAB® に付属の関数 vdp1000 が方程式をエンコードします。

function dydt = vdp1000(t,y)
%VDP1000  Evaluate the van der Pol ODEs for mu = 1000.
%
%   See also ODE15S, ODE23S, ODE23T, ODE23TB.

%   Jacek Kierzenka and Lawrence F. Shampine
%   Copyright 1984-2014 The MathWorks, Inc.

dydt = [y(2); 1000*(1-y(1)^2)*y(2)-y(1)];

既定の相対許容誤差および絶対許容誤差 (それぞれ 1e-3 および 1e-6) によって ode45 を使用し、この方程式を求解すると非常に時間がかかります。また、解のプロットにも数分かかります。許容誤差内に収めるためのスティッフな領域が原因で、ode45 で積分を完了するには数百万ものタイムステップが必要です。

次のプロットは ode45 で得られた解ですが、この計算には長い時間がかかります。スティッフな領域を通過するために、膨大な数のタイムステップが必要であることがわかります。

ode23t ソルバーを使用してスティッフな方程式を解き、解 y の 1 列目を時点 t に対してプロットします。ode23t ソルバーは ode45 よりもはるかに少ないステップでスティッフな領域を通過します。

[t,y] = ode23t(@vdp1000,[0 3000],[2 0]);
plot(t,y(:,1),'-o')

ODE 関数に追加パラメーターを渡す

スクリプトを開く

ode23t は、2 つの入力引数 t と y を使用する関数にのみ使用できます。しかし、関数の外部で定義した追加のパラメーターを、関数ハンドルを指定するタイミングで渡すことができます。

次の ODE を解きます。

$y'' = \frac{A}{B} t y.$

この方程式を連立 1 階方程式として書き直すと次のようになります。

$\begin{array}{cl} y'_1 &= y_2\\ y'_2 &= \frac{A}{B} t y_1.
\end{array}$

odefcn.m はこの連立方程式を 4 つの入力引数 (t、y、A、B) を受け入れる関数として表します。

function dydt = odefcn(t,y,A,B)
dydt = zeros(2,1);
dydt(1) = y(2);
dydt(2) = (A/B)*t.*y(1);

ode23t を使用して ODE を解きます。事前定義された A と B の値を odefcn に渡す関数ハンドルを指定します。

A = 1;
B = 2;
tspan = [0 5];
y0 = [0 0.01];
[t,y] = ode23t(@(t,y) odefcn(t,y,A,B), tspan, y0);

結果をプロットします。

plot(t,y(:,1),'-o',t,y(:,2),'-.')

スティッフ ODE ソルバーの比較

ライブスクリプトを開く

ode15s ソルバーは、ほとんどのスティッフな問題に適する最初の選択肢です。しかし、特定のタイプの問題に対しては他のスティッフソルバーの方が効率的な場合もあります。この例では、4 つすべてのスティッフ ODE ソルバーを使用してスティッフなテスト方程式を解きます。

次のテスト方程式を考えます。

$y^{'} = - λ y .$

この方程式は $λ$ の絶対値が大きくなるにつれてスティッフ性が増大します。 $λ = 1 \times 1 0^{9}$ と初期条件 $y (0) = 1$ を、時間区間 [0 0.5] にわたって使用します。これらの値を使用すると、問題が十分にスティッフであるため、ode45 および ode23 では方程式の積分が困難です。また、odeset を使用して定数ヤコビ行列 $J = \frac{\partial f}{\partial y} = - λ$ を渡し、ソルバー統計の表示をオンにします。

lambda = 1e9;
y0 = 1;
tspan = [0 0.5];
opts = odeset('Jacobian',-lambda,'Stats','on');

ode15s、ode23s、ode23t、ode23tb を使用して方程式を解きます。比較のサブプロットを作成します。

subplot(2,2,1)
tic, ode15s(@(t,y) -lambda*y, tspan, y0, opts), toc

104 successful steps
1 failed attempts
212 function evaluations
0 partial derivatives
21 LU decompositions
210 solutions of linear systems
Elapsed time is 3.261408 seconds.

title('ode15s')
subplot(2,2,2)
tic, ode23s(@(t,y) -lambda*y, tspan, y0, opts), toc

63 successful steps
0 failed attempts
191 function evaluations
0 partial derivatives
63 LU decompositions
189 solutions of linear systems
Elapsed time is 0.633155 seconds.

title('ode23s')
subplot(2,2,3)
tic, ode23t(@(t,y) -lambda*y, tspan, y0, opts), toc

95 successful steps
0 failed attempts
125 function evaluations
0 partial derivatives
28 LU decompositions
123 solutions of linear systems
Elapsed time is 0.372408 seconds.

title('ode23t')
subplot(2,2,4)
tic, ode23tb(@(t,y) -lambda*y, tspan, y0, opts), toc

71 successful steps
0 failed attempts
167 function evaluations
0 partial derivatives
23 LU decompositions
236 solutions of linear systems
Elapsed time is 0.601404 seconds.

title('ode23tb')

Figure contains 4 axes objects. Axes object 1 with title ode15s contains 2 objects of type line. Axes object 2 with title ode23s contains 2 objects of type line. Axes object 3 with title ode23t contains 2 objects of type line. Axes object 4 with title ode23tb contains 2 objects of type line.

すべてのスティッフソルバーは良好に動作しますが、この特定の問題では ode23s が最小ステップ数、最短時間で積分を完了します。定数ヤコビ行列が指定されているため、どのソルバーも解を求めるために偏導関数を計算する必要はありません。通常、ode23s はステップごとにヤコビ行列を評価するため、ヤコビ行列の指定は ode23s に最も利点があります。

一般のスティッフな問題の場合、スティッフソルバーのパフォーマンスは問題の形式と指定されたオプションによって異なります。ヤコビ行列やスパースパターンを指定すると、スティッフな問題に対するソルバーの効率が常に向上します。しかし、各スティッフソルバーでのヤコビ行列の扱いは異なるため、向上の程度は大きく異なる可能性があります。実際、連立方程式が非常に大きい場合、あるいは何回も解く必要がある場合は、実行時間を最短にするためにさまざまなソルバーのパフォーマンスを調べる価値があります。

入力引数

すべて折りたたむ

`odefun` — 解を求める関数
関数ハンドル

解を求める関数。積分する関数を定義する関数ハンドルとして指定します。

スカラー t および列ベクトル y をとる関数 dydt = odefun(t,y) は、データ型が single または double で $f (t, y)$ に対応する列ベクトル dydt を返さなければなりません。odefun は、t と y のいずれかの引数が関数で使用されない場合でも、両方の入力引数を受け入れなければなりません。

たとえば、 $y' = 5 y - 3$ を解くには、次の関数を使用します。

function dydt = odefun(t,y)
dydt = 5*y-3;
end

連立方程式の場合、odefun の出力はベクトルです。ベクトルの各要素は 1 つの方程式の右辺の計算値です。たとえば、次の 2 つを含む連立方程式について考えます。

$\begin{array}{l} y'_{1} = y_{1} + 2 y_{2} \\ y'_{2} = 3 y_{1} + 2 y_{2} \end{array}$

各タイムステップで各方程式の右辺の値を計算する関数は以下のとおりです。

function dydt = odefun(t,y)
dydt = zeros(2,1);
dydt(1) = y(1)+2*y(2);
dydt(2) = 3*y(1)+2*y(2);
end

関数 odefun に追加パラメーターを指定する方法の詳細については、関数のパラメーター化を参照してください。

例: @myFcn

データ型: function_handle

`tspan` — 積分区間
ベクトル

積分区間。ベクトルとして指定します。少なくとも、tspan は開始時点と終了時点を指定する 2 要素ベクトル [t0 tf] でなければなりません。t0 と tf の間の特定時点における解を取得するには、[t0,t1,t2,...,tf] の形式の長いベクトルを使用します。tspan の要素は、単調増加または単調減少でなければなりません。

ソルバーは開始時点 tspan(1) で y0 によって指定される初期条件を設定し、tspan(1) から tspan(end) まで積分します。

tspan に 2 つの要素がある場合 ([t0 tf])、ソルバーは区間内の個々の内部積分ステップで計算した解を返します。
tspan に 2 つを超える要素がある場合 ([t0,t1,t2,...,tf])、ソルバーは指定された各点で計算した解を返します。ただし、ソルバーは tspan で指定された各点に正確にステップするわけではありません。代わりに、ソルバーは独自の内部ステップを使用して解を計算し、tspan 内の要求された点で解を評価します。指定された点で出力された解の精度の次数は、各内部ステップで計算された解と同じです。
中間点をいくつか指定しても計算効率にほとんど影響しませんが、大規模な方程式の場合はメモリ管理に影響を及ぼす可能性があります。

ソルバーは tspan の値を使用して InitialStep と MaxStep に適した値を計算します。

tspan に複数の中間点が含まれる場合 ([t0,t1,t2,...,tf])、指定した点は問題のスケールの目安となり、これはソルバーが使用する InitialStep の値に影響することがあります。そのため、ソルバーで得られる解は、tspan を 2 要素ベクトルとして指定するか、中間点を含むベクトルとして指定するかによって異なる場合があります。
tspan の最初と最後の値は、最大ステップサイズ MaxStep の計算に使用されます。そのため、tspan の最初または最後の値を変更すると、ソルバーが別のステップシーケンスを使用する可能性があり、そのため解が変わることがあります。

例: [1 10]

例: [1 3 5 7 9 10]

データ型: single | double

`y0` — 初期条件
ベクトル

初期条件。ベクトルとして指定します。odefun に定義された各方程式の初期条件を y0 に含めるために、y0 は odefun のベクトル出力と同じ長さでなければなりません。

データ型: single | double

`options` — オプション構造体
構造体配列

オプション構造体。構造体配列として指定します。options 構造体の作成または変更には、関数 odeset を使用します。各 ODE ソルバーと互換性のあるオプションの一覧については、ODE オプションの概要を参照してください。

例: options = odeset('RelTol',1e-5,'Stats','on','OutputFcn',@odeplot) は、相対許容誤差 1e-5 を指定し、ソルバー統計の表示をオンにして、解の計算時に解をプロットする出力関数 @odeplot を指定します。

データ型: struct

出力引数

すべて折りたたむ

`t` — 評価点
列ベクトル

評価点。列ベクトルとして返されます。

tspan に 2 つの要素がある場合 ([t0 tf])、t には積分の実行に使用される内部評価点が含まれます。
tspan に 2 つより多い要素が含まれる場合、t は tspan と同じです。

`y` — 解
配列

解。配列として返されます。y の各行は、t の対応する行に返される値での解です。

`te` — イベント時点
列ベクトル

イベント時点。列ベクトルとして返されます。te のイベント時点は ye に返された解に対応し、ie は発生したイベントを指定します。

`ye` — イベント時点での解
配列

イベント時点での解。配列として返されます。te のイベント時点は ye に返された解に対応し、ie は発生したイベントを指定します。

`ie` — トリガーされるイベント関数のインデックス
列ベクトル

トリガーされるイベント関数のインデックス。列ベクトルとして返されます。te のイベント時点は ye に返された解に対応し、ie は発生したイベントを指定します。

`sol` — 評価対象の構造体
構造体配列

評価対象の構造体。構造体配列として返されます。この構造体を関数 deval と共に使用して区間 [t0 tf] の任意の点で解を評価します。構造体配列 sol は、常に以下のフィールドを含みます。

構造体フィールド	説明
`sol.x`	ソルバーによって選択されたステップの行ベクトル。
`sol.y`	解。各列の `sol.y(:,i)` には、時点 `sol.x(i)` での解が含まれます。
`sol.solver`	ソルバー名。

さらに、odeset の Events オプションを指定してイベントが検出された場合、sol は以下のフィールドも含みます。

構造体フィールド	説明
`sol.xe`	イベントが発生した点。`sol.xe(end)` には、終了イベントの厳密な点 (存在する場合) が含まれます。
`sol.ye`	`sol.xe` のイベントに対応する解。
`sol.ie`	`Events` オプションに指定された関数により返されるベクトルのインデックス。値は、どのイベントをソルバーが検出したかを示します。

アルゴリズム

関数 ode23t は、"フリー" 内挿を利用して台形則を実行します。問題が中程度にスティッフであり、数値的減衰のない解が必要な場合には、ode15s よりもこのソルバーが推奨されます。ode23t は微分代数方程式 (DAE) を解くこともできます [1]、[2]。

参照

[1] Shampine, L. F., M. W. Reichelt, and J.A. Kierzenka, “Solving Index-1 DAEs in MATLAB and Simulink”, SIAM Review, Vol. 41, 1999, pp. 538–552.

[2] Shampine, L. F. and M. E. Hosea, “Analysis and Implementation of TR-BDF2,” Applied Numerical Mathematics 20, 1996.

バージョン履歴

R2006a より前に導入

参考

ode15s | odeset | odeget | deval

ode23t

構文

説明

例

単一解要素をもつ ODE

スティッフな ODE の求解

ODE 関数に追加パラメーターを渡す

スティッフ ODE ソルバーの比較

入力引数

odefun — 解を求める関数 関数ハンドル

tspan — 積分区間 ベクトル

y0 — 初期条件 ベクトル

options — オプション構造体 構造体配列

出力引数

t — 評価点 列ベクトル

y — 解 配列

te — イベント時点 列ベクトル

ye — イベント時点での解 配列

ie — トリガーされるイベント関数のインデックス 列ベクトル

sol — 評価対象の構造体 構造体配列

アルゴリズム

参照

バージョン履歴

参考

トピック

`odefun` — 解を求める関数
関数ハンドル

`tspan` — 積分区間
ベクトル

`y0` — 初期条件
ベクトル

`options` — オプション構造体
構造体配列

`t` — 評価点
列ベクトル

`y` — 解
配列

`te` — イベント時点
列ベクトル

`ye` — イベント時点での解
配列

`ie` — トリガーされるイベント関数のインデックス
列ベクトル

`sol` — 評価対象の構造体
構造体配列