微分代数方程式 (DAE) の求解

微分代数方程式とは

微分代数方程式とは、従属変数の導関数が 1 つ以上その方程式には存在しない微分方程式の一種です。導関数が含まれない方程式内の変数は "代数変数" と呼ばれ、代数変数が存在すると、その方程式は陽的な形式 $y' = f (t, y)$ で記述できないことを意味します。代わりに、次の形式を使用して DAE の解を求めます。

ソルバー ode15s および ode23t では、特異質量行列 $M (t, y) y' = f (t, y)$ を使用して、指数が 1 の線形陰的な問題の解を求めることができます。これには、次の形式の半陽的な DAE も含まれます。
$\begin{matrix} y' = f (t, y, z) \\ 0 = g (t, y, z) . \end{matrix}$
この形式では、主対角に 1 つ以上のゼロがあるため、代数変数を使用すると特異質量行列になります。
$M y' = (\begin{matrix} y'_{1} & 0 & \dots & 0 \\ 0 & y'_{2} & 0 & ⋮ \\ ⋮ & 0 & ⋱ & 0 \\ 0 & \dots & 0 & 0 \end{matrix}) .$
既定では、DAE 系を検出するために、ソルバーによって質量行列の特異性が自動的にテストされます。特異性を事前に把握している場合は、odeset の MassSingular オプションを 'yes' に設定できます。DAE では、odeset の InitialSlope プロパティを使用して、 $y'_{0}$ の初期条件の推定値をソルバーに提供することもできます。これは、ソルバー呼び出しでの $y_{0}$ の通常の初期条件に加えて指定されます。
ode15i ソルバーを使用すると、次のように完全陰的な形式で、より一般的な DAE の解を求めることができます。
$f (t, y, y') = 0 .$
完全陰的な形式では、代数変数を使用すると特異ヤコビ行列になります。これは、その変数の導関数が方程式にないため、行列内の少なくとも 1 つの列が必ずすべてゼロになることが理由です。
$J = \partial f / \partial y' = (\begin{matrix} \frac{\partial f_{1}}{\partial y'_{1}} & \dots & \frac{\partial f_{1}}{\partial y'_{n}} \\ ⋮ & ⋱ & ⋮ \\ \frac{\partial f_{m}}{\partial y'_{1}} & \dots & \frac{\partial f_{m}}{\partial y'_{n}} \end{matrix})$
ode15i ソルバーでは、 $y'_{0}$ および $y_{0}$ の両方に対し初期条件を指定する必要があります。また、他の ODE ソルバーとは異なり、ode15i では方程式をエンコードする関数で入力をもう 1 つ受け入れる必要があります。つまり、odefun(t,y,yp) となります。

DAE はさまざまな種類の系で使用されます。これは物理的な保存則では $x + y + z = 0$ のような形式がよく扱われるためです。x、x'、y および y' が方程式内で陽的に定義されている場合、z' の式を使用しなくても、この保存方程式だけで z の解を求められます。

整合性のある初期条件

DAE の解を求める際に、 $y'_{0}$ および $y_{0}$ の両方に対して初期条件を指定できます。ode15i ソルバーでは両方の初期条件を入力引数として指定する必要があります。ode15s ソルバーと ode23t ソルバーでは、 $y'_{0}$ の初期条件は任意です (ただし、odeset の InitialSlope オプションを使用して指定できます)。いずれの場合も、指定する初期条件は解を求める方程式との整合性がなくてもかまいません。相互に競合する初期条件は "不整合" であると見なされます。初期条件の処理方法はソルバーによって異なります。

ode15s および ode23t — $y'_{0}$ に対して初期条件を指定しない場合、 $y_{0}$ に対し提供された初期条件に基づいて、整合性のある初期条件がソルバーで自動的に計算されます。 $y'_{0}$ に対して不整合な初期条件を指定すると、ソルバーはこれらを推定値として扱い、推定値に近い整合的な値の計算を試行し、問題の求解を続けます。
ode15i — このソルバーに提供する初期条件には整合性がなければなりませんが、ode15i では、提供された値に対する整合性チェックを行いません。この目的のために、補助関数 decic で整合性のある初期条件を計算してください。

微分指数

DAE は "微分指数" があることが特徴です。これはその特異度を示します。方程式を微分すると代数変数を除外でき、これを必要な回数行うと、その方程式は陽的 ODE 系の形式になります。DAE 系の微分指数は、等価な陽的 ODE 系として表すために使用しなければならない導関数の数を示します。したがって、ODE の微分指数は 0 になります。

指数が 1 の DAE の例を次に示します。

$y (t) = k (t) .$

この方程式の場合、導関数を 1 つ使用すると、陽的 ODE の形式が得られます。

$y' = k' (t) .$

指数が 2 の DAE の例を次に示します。

$\begin{array}{l} y'_{1} = y_{2} \\ 0 = k (t) - y_{1} . \end{array}$

これらの方程式を陽的 ODE の形式に書き換えるには、導関数が 2 つ必要です。

$\begin{array}{l} y'_{1} = k' (t) \\ y'_{2} = k'' (t) . \end{array}$

ode15s ソルバーと ode23t ソルバーで解くことができるのは、指数 1 の DAE のみです。方程式の指数が 2 以上の場合は、指数が 1 の等価な DAE 系としてこれらの方程式を書き換える必要があります。導関数を使用して、DAE 系を指数が 1 の等価な DAE 系として書き換えることは常に可能です。ただし、代数方程式をその導関数に置き換えると、一部の制約が排除されてしまう可能性があることに注意してください。方程式に元の制約が存在しなくなると、数値解が変動することがあります。

Symbolic Math Toolbox™ を所有している場合、詳細については微分代数方程式 (DAE) の求解 (Symbolic Math Toolbox)を参照してください。

非負の制約を課す

odeset のほどんとのオプションは DAE ソルバー ode15s、ode23t、ode15i で想定どおりに機能します。ただし、NonNegative オプションを使用する場合にのみ、1 つの顕著な例外が発生します。NonNegative オプションは質量行列をもつ問題に適用される陰的ソルバー (ode15s、ode23t、ode23tb) をサポートしません。したがって、このオプションを使用して、必ず特異質量行列をもつ DAE 問題に非負の制約を課すことはできません。詳細については、[1]を参照してください。

Robertson 問題を半陽的な微分代数方程式 (DAE) として求解

スクリプトを開く

この例では、ODE 系を微分代数方程式 (DAE) 系として再定式化します。hb1ode.m に含まれる Robertson 問題は、スティッフ ODE の解を求めるプログラムに対する古典的なテスト問題です。方程式系は次のとおりです。

$\begin{array}{cl} y'_1 &= -0.04y_1 + 10^4 y_2y_3\\ y'_2 &= 0.04y_1 -
10^4 y_2y_3- (3 \times 10^7)y_2^2\\ y'_3 &= (3 \times
10^7)y_2^2.\end{array}$

hb1ode では、初期条件、、およびを使用して、この ODE 系の定常状態の解を求めます。ただし、これらの方程式は次の線形保存則も満たします。

この解と初期条件に基づくと、保存則は次のようになります。

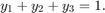
この保存則を使用しての状態を決定することにより、この方程式系を DAE 系として書き換えることができます。これにより、問題が次の DAE 系として再定式化されます。

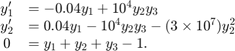
$\begin{array}{cl} y'_1 &= -0.04y_1 + 10^4 y_2y_3\\ y'_2 &= 0.04y_1 -
10^4 y_2y_3-(3 \times 10^7)y_2^2\\ 0 &= y_1 + y_2 + y_3 - 1.\end{array}$

これを ODE 系にするために必要なの導関数は 1 つのみであるため、この系の微分インデックスは 1 です。したがって、この系の解を求めるためにこれ以上の変換は不要です。

関数 robertsdae でこの DAE 系をエンコードします。現在のフォルダーに robertsdae.m を保存して、この例を実行します。

function out = robertsdae(t,y)
out = [-0.04*y(1) + 1e4*y(2).*y(3)
   0.04*y(1) - 1e4*y(2).*y(3) - 3e7*y(2).^2
   y(1) + y(2) + y(3) - 1 ];

Robertson 問題のこの定式化を含む完全なサンプルコードは hb1dae.m として提供されています。

ode15s を使用して、この DAE 系の解を求めます。保存則に基づくと、矛盾のない y0 の初期条件は明白です。odeset を使用して、オプションを次のように設定します。

定質量行列を使用して、連立方程式の左辺を表します。

$\left( \begin{array}{c} y'_1\\ y'_2\\ 0 \end{array} \right) = M y'
\rightarrow M = \left( \begin{array}{ccc} 1 & 0 & 0\\ 0 & 1 & 0\\ 0 & 0 &
0 \end{array} \right)$

相対許容誤差を 1e-4 に設定します。
2 番目の解の要素に絶対許容誤差 1e-10 を使用します。これはスケールが他の要素とは著しく異なるためです。
DAE の自動検出をテストするために、'MassSingular' オプションを既定値 'maybe' のままにします。

y0 = [1; 0; 0];
tspan = [0 4*logspace(-6,6)];
M = [1 0 0; 0 1 0; 0 0 0];
options = odeset('Mass',M,'RelTol',1e-4,'AbsTol',[1e-6 1e-10 1e-6]);
[t,y] = ode15s(@robertsdae,tspan,y0,options);

解をプロットします。

y(:,2) = 1e4*y(:,2);
semilogx(t,y);
ylabel('1e4 * y(:,2)');
title('Robertson DAE problem with a Conservation Law, solved by ODE15S');

参照

[1] Shampine, L.F., S. Thompson, J.A. Kierzenka, and G.D. Byrne. “Non-Negative Solutions of ODEs.” Applied Mathematics and Computation 170, no. 1 (November 2005): 556–569. https://doi.org/10.1016/j.amc.2004.12.011.

参考

ode15s | ode23t | ode15i | odeset

外部の Web サイト

Solving Index-1 DAEs in MATLAB and Simulink