微分代数方程式 (DAE) の求解

この例では、MATLAB® と Symbolic Math Toolbox™ を使用して微分代数方程式 (DAE) を解く方法を示します。

関数 (状態変数) $\mathit{x}\left(\mathit{t}\right)=\left[{\mathit{x}}_1\left(\mathit{t}\right),...,{\mathit{x}}_{\mathit{n}}\left(\mathit{t}\right)\right]$ を含む微分代数方程式は、次のような形をもちます。

$$F(t,x(t),\underset{}{\overset{\dot{}}{x}}(t))=0$$

ここで、$\mathit{t}$ は独立変数です。方程式の数 $\mathit{F}=\left[{\mathit{F}}_1,...,{\mathit{F}}_{\mathit{n}}\right]$ は状態変数の数 $\mathit{x}\left(\mathit{t}\right)=\left[{\mathit{x}}_1\left(\mathit{t}\right),...,{\mathit{x}}_{\mathit{n}}\left(\mathit{t}\right)\right]$ と一致しなければなりません。

ほとんどの DAE 系は ode15i のような MATLAB ソルバーの入力として直接与えるのに適した形式になっていないため、Symbolic Math Toolbox の機能を用いてはじめに適切な形式に変換します。この機能は DAE の微分指数 (系を ODE に簡約するのに必要な微分の数) を 1 または 0 に減らしてから、DAE 系を MATLAB ソルバーに適した数値関数ハンドルに変換します。次に、MATLAB ソルバーである ode15i、ode15s、ode23t のいずれかを使用して DAE を求解します。

これらの手順を完了することで DAE 系を解きます。

手順 1: 方程式と変数の指定

次の図の振子の DAE を解くことで DAE ワークフローを示します。

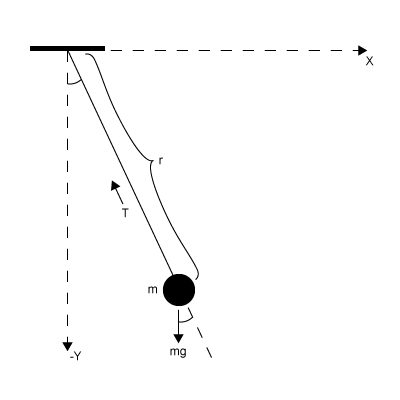
状態変数は次のとおりです。

• 振子の水平位置 $\mathit{x}\left(\mathit{t}\right)$

• 振子の垂直位置 $\mathit{y}\left(\mathit{t}\right)$

• 振子の飛び出しを妨げる力 $\mathit{T}\left(\mathit{t}\right)$

変数は次のとおりです。

• 振子の質量 $\mathit{m}$

• 振子の長さ $\mathit{r}$

• 重力定数 $\mathit{g}$

DAE 系は次のとおりです。

$$\begin{array}{l}m\frac{d^{2}x}{d{t}^2}=T\left(t\right)\frac{x\left(t\right)}{r}\\ m\frac{d^{2}y}{d{t}^2}=T\left(t\right)\frac{y\left(t\right)}{r}-mg\\ x{\left(t\right)}^2+y{\left(t\right)}^2=r^2\end{array}$$

syms を用いて独立変数と状態変数を指定します。

syms x(t) y(t) T(t) m r g

== 演算子を使用して方程式を指定します。

eqn1 = m*diff(x(t), 2) == T(t)/r*x(t);
eqn2 = m*diff(y(t), 2) == T(t)/r*y(t) - m*g;
eqn3 = x(t)^2 + y(t)^2 == r^2;
eqns = [eqn1 eqn2 eqn3];

状態変数を列ベクトルにします。参照するために元の変数の数を格納します。

vars = [x(t); y(t); T(t)];
origVars = length(vars);

手順 2: 微分の階数の簡約

2.1 (オプション) 変数の発生範囲の確認

この手順は "オプション" です。接続行列を見ることで DAE 系での変数の発生箇所を確認できます。この手順により、入力からは発生しないすべての変数を発見し、vars ベクトルから取り除くことができます。

incidenceMatrix を使用して新しい系の接続行列を表示します。incidenceMatrix の出力は各方程式を行に、各変数を列にもちます。この系には 3 つの方程式と 3 つの状態変数が含まれるため、incidenceMatrix は 3 行 3 列の行列を返します。行列には 1 と 0 があります。ここで 1 は状態変数の出現を表します。たとえば、位置 (2,3) の 1 は、2 番目の方程式には 3 番目の状態変数 T(t) が含まれることを意味します。

M = incidenceMatrix(eqns,vars)

M = 3×3

     1     0     1
     0     1     1
     1     1     0

接続行列のある列がすべて 0 だった場合は、その状態変数が DAE 系に出現しないため取り除かなければなりません。

2.2 微分の階数の簡約

DAE 系の "微分階数" とは、その方程式の最高微分階数です。MATLAB を使用して DAE を解くには、微分階数を 1 に簡約する必要があります。ここで、1 番目および 2 番目の方程式には x(t) および y(t) の 2 次導関数が含まれています。したがって、微分階数は 2 です。

reduceDifferentialOrder を使用して系を 1 階の系に簡約します。関数 reduceDifferentialOrder は導関数を Dxt(t) や Dyt(t) のような新しい変数に置き換えます。eqns の式の右辺は 0 です。

[eqns,vars] = reduceDifferentialOrder(eqns,vars)

eqns = 
$$\left(\begin{array}{c}m\hspace{0.17em}\frac{\partial }{\partial t}\mathrm{ }\mathrm{Dxt}\left(t\right)-\frac{T\left(t\right)\hspace{0.17em}x\left(t\right)}{r}\\ g\hspace{0.17em}m+m\hspace{0.17em}\frac{\partial }{\partial t}\mathrm{ }\mathrm{Dyt}\left(t\right)-\frac{T\left(t\right)\hspace{0.17em}y\left(t\right)}{r}\\ -r^2+{x\left(t\right)}^2+{y\left(t\right)}^2\\ \mathrm{Dxt}\left(t\right)-\frac{\partial }{\partial t}\mathrm{ }x\left(t\right)\\ \mathrm{Dyt}\left(t\right)-\frac{\partial }{\partial t}\mathrm{ }y\left(t\right)\end{array}\right)$$

vars = 
$$\left(\begin{array}{c}x\left(t\right)\\ y\left(t\right)\\ T\left(t\right)\\ \mathrm{Dxt}\left(t\right)\\ \mathrm{Dyt}\left(t\right)\end{array}\right)$$

手順 3: 微分指数を確認して減らす

3.1 系の微分指数の確認

isLowIndexDAEを使用して DAE 系の微分指数を確認します。指数が 0 または 1 である場合、isLowIndexDAE は logical 1 (true) を返し、手順 3.2 を飛ばして手順 4 の次の内容に進むことができます。「DAE 系の MATLAB 関数ハンドルへの変換」。ここで、isLowIndexDAE が logical 0 (false) を返します。これは微分指数が 1 よりも大きいため、減らす必要があることを意味します。

isLowIndexDAE(eqns,vars)

ans = logical
   0

3.2 reduceDAEIndex で微分指数を減らす

微分指数を減らすために、関数 reduceDAEIndex は与えられた方程式から導出される新しい方程式を追加し、高次の導関数を新しい変数に置き換えます。reduceDAEIndex が失敗して警告が発生した場合は、ワークフロー半線形 DAE 系の求解に記載されているとおり、代替となる関数 reduceDAEToODE を使用します。

eqns および vars の DAE の微分指数を減らします。

[DAEs,DAEvars] = reduceDAEIndex(eqns,vars)

DAEs = 
$$\left(\begin{array}{c}m\hspace{0.17em}\mathrm{Dxtt}\left(t\right)-\frac{T\left(t\right)\hspace{0.17em}x\left(t\right)}{r}\\ g\hspace{0.17em}m+m\hspace{0.17em}\mathrm{Dytt}\left(t\right)-\frac{T\left(t\right)\hspace{0.17em}y\left(t\right)}{r}\\ -r^2+{x\left(t\right)}^2+{y\left(t\right)}^2\\ \mathrm{Dxt}\left(t\right)-{\mathrm{Dxt}}_1\left(t\right)\\ \mathrm{Dyt}\left(t\right)-{\mathrm{Dyt}}_1\left(t\right)\\ 2\hspace{0.17em}{\mathrm{Dxt}}_1\left(t\right)\hspace{0.17em}x\left(t\right)+2\hspace{0.17em}{\mathrm{Dyt}}_1\left(t\right)\hspace{0.17em}y\left(t\right)\\ 2\hspace{0.17em}y\left(t\right)\hspace{0.17em}\frac{\partial }{\partial t}\mathrm{ }{\mathrm{Dyt}}_1\left(t\right)+2\hspace{0.17em}{{\mathrm{Dxt}}_1\left(t\right)}^2+2\hspace{0.17em}{{\mathrm{Dyt}}_1\left(t\right)}^2+2\hspace{0.17em}\mathrm{Dxt1t}\left(t\right)\hspace{0.17em}x\left(t\right)\\ \mathrm{Dxtt}\left(t\right)-\mathrm{Dxt1t}\left(t\right)\\ \mathrm{Dytt}\left(t\right)-\frac{\partial }{\partial t}\mathrm{ }{\mathrm{Dyt}}_1\left(t\right)\\ {\mathrm{Dyt}}_1\left(t\right)-\frac{\partial }{\partial t}\mathrm{ }y\left(t\right)\end{array}\right)$$

DAEvars = 
$$\left(\begin{array}{c}x\left(t\right)\\ y\left(t\right)\\ T\left(t\right)\\ \mathrm{Dxt}\left(t\right)\\ \mathrm{Dyt}\left(t\right)\\ \mathrm{Dytt}\left(t\right)\\ \mathrm{Dxtt}\left(t\right)\\ {\mathrm{Dxt}}_1\left(t\right)\\ {\mathrm{Dyt}}_1\left(t\right)\\ \mathrm{Dxt1t}\left(t\right)\end{array}\right)$$

reduceDAEIndex でエラーや警告が発生した場合は、半線形 DAE 系の求解に記述されたワークフローを代わりに使用します。

多くの場合、reduceDAEIndex は削除できる冗長な方程式や変数を挿入します。reduceRedundancies を使用して冗長な方程式と変数を削除します。

[DAEs,DAEvars] = reduceRedundancies(DAEs,DAEvars)

DAEs = 
$$\left(\begin{array}{c}-\frac{T\left(t\right)\hspace{0.17em}x\left(t\right)-m\hspace{0.17em}r\hspace{0.17em}\mathrm{Dxtt}\left(t\right)}{r}\\ \frac{g\hspace{0.17em}m\hspace{0.17em}r-T\left(t\right)\hspace{0.17em}y\left(t\right)+m\hspace{0.17em}r\hspace{0.17em}\mathrm{Dytt}\left(t\right)}{r}\\ -r^2+{x\left(t\right)}^2+{y\left(t\right)}^2\\ 2\hspace{0.17em}\mathrm{Dxt}\left(t\right)\hspace{0.17em}x\left(t\right)+2\hspace{0.17em}\mathrm{Dyt}\left(t\right)\hspace{0.17em}y\left(t\right)\\ 2\hspace{0.17em}{\mathrm{Dxt}\left(t\right)}^2+2\hspace{0.17em}{\mathrm{Dyt}\left(t\right)}^2+2\hspace{0.17em}\mathrm{Dxtt}\left(t\right)\hspace{0.17em}x\left(t\right)+2\hspace{0.17em}\mathrm{Dytt}\left(t\right)\hspace{0.17em}y\left(t\right)\\ \mathrm{Dytt}\left(t\right)-\frac{\partial }{\partial t}\mathrm{ }\mathrm{Dyt}\left(t\right)\\ \mathrm{Dyt}\left(t\right)-\frac{\partial }{\partial t}\mathrm{ }y\left(t\right)\end{array}\right)$$

DAEvars = 
$$\left(\begin{array}{c}x\left(t\right)\\ y\left(t\right)\\ T\left(t\right)\\ \mathrm{Dxt}\left(t\right)\\ \mathrm{Dyt}\left(t\right)\\ \mathrm{Dytt}\left(t\right)\\ \mathrm{Dxtt}\left(t\right)\end{array}\right)$$

新しい系の微分指数を確認します。これで isLowIndexDAE は logical 1 (true) を返すようになります。つまり、系の微分指数は 0 または 1 です。

isLowIndexDAE(DAEs,DAEvars)

ans = logical
   1

手順 4: DAE 系の MATLAB 関数ハンドルへの変換

この手順では MATLAB ODE ソルバーである ode15i 用の関数ハンドルを作成します。これは汎用ソルバーです。ode15s や ode23t のような質量行列に特化したソルバーを使用するには、質量行列ソルバーを使用した DAE の求解およびODE ソルバーの選択を参照してください。

reduceDAEIndex は DAEs の方程式のベクトルと DAEvars の変数のベクトルを出力します。ode15i を使用するには、DAE 系を表す関数ハンドルが必要です。

はじめに、DAEs の方程式には変数のベクトル DAEvars で指定されていないシンボリック パラメーターが含まれても構いません。DAEs および DAEvars から得られた symvar の出力に対して setdiff を使用して、これらのパラメーターを求めます。

pDAEs = symvar(DAEs);
pDAEvars = symvar(DAEvars);
extraParams = setdiff(pDAEs,pDAEvars)

extraParams = $$\left(\begin{array}{ccc}g& m& r\end{array}\right)$$

別途指定する必要のあるパラメーターは質量 m、半径 r、および重力定数 g です。

daeFunction を使用して関数ハンドルを作成します。daeFunction への追加の入力引数として、シンボリック パラメーターを別途指定します。

f = daeFunction(DAEs,DAEvars,g,m,r);

以降のワークフローは純粋に数値的です。パラメーター値を設定して ode15i の関数ハンドルを作成します。

g = 9.81;
m = 1;
r = 1;
F = @(t,Y,YP) f(t,Y,YP,g,m,r);

手順 5: ソルバーの初期条件を求める

ソルバー ode15i は、関数ハンドル内のあらゆる変数に対して初期値を必要とします。MATLAB 関数 decic を使用して、方程式を満たすような初期値を求めます。decic は推測された (方程式を満たさない可能性のある) 初期条件も取り扱うことができ、それらの推測を使用して充足する初期条件を求めようとします。decic は失敗することもあり、そのような場合は問題に対し整合性のある初期値を手動で設定する必要があります。

はじめに、DAEvars の変数をチェックします。

DAEvars

DAEvars = 
$$\left(\begin{array}{c}x\left(t\right)\\ y\left(t\right)\\ T\left(t\right)\\ \mathrm{Dxt}\left(t\right)\\ \mathrm{Dyt}\left(t\right)\\ \mathrm{Dytt}\left(t\right)\\ \mathrm{Dxtt}\left(t\right)\end{array}\right)$$

ここで、Dxt(t) は x(t) の 1 次導関数、Dytt(t) は y(t) の 2 次導関数、以下同様です。7 × 1 ベクトルには 7 個の変数が含まれます。したがって、変数の初期値とその導関数の推測も 7 × 1 ベクトルでなければなりません。

振子の初期角変位が 30° つまり pi/6、座標の原点が振子のつり下げ点にあるとします。半径 r は 1 であるため、初期水平位置 x(t) は r*sin(pi/6) です。初期垂直位置 y(t) は -r*cos(pi/6) です。ベクトル y0est におけるこれらの変数の初期値を指定します。

残りの変数の初期値を任意に設定し、その導関数を 0 に設定します。これらは良い推測ではありません。ただし、この問題にはこれで十分です。問題において decic エラーが発生した場合は、より良い推測を与えてからdecicを参照してください。

y0est = [r*sin(pi/6); -r*cos(pi/6); 0; 0; 0; 0; 0];
yp0est = zeros(7,1);

数値検索における数値的許容誤差を指定するオプション セットを作成します。

opt = odeset('RelTol', 10.0^(-7),'AbsTol',10.0^(-7));

decic を使用して、変数とその導関数で整合性のある初期値を求めます。

[y0,yp0] = decic(F,0,y0est,[],yp0est,[],opt)

y0 = 7×1

    0.4771
   -0.8788
   -8.6214
         0
   -0.0000
   -2.2333
   -4.1135

yp0 = 7×1

         0
   -0.0000
         0
         0
   -2.2333
         0
         0

手順 6: ode15i を使用した DAE の求解

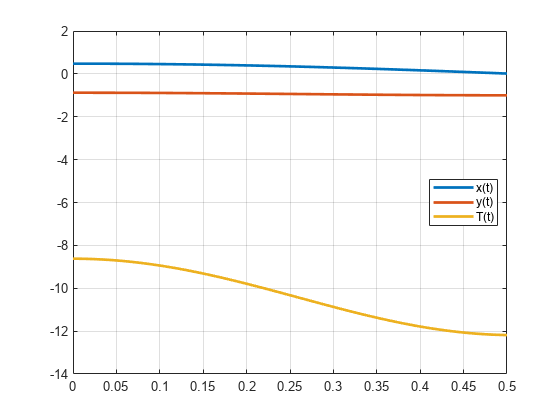
系を時間範囲 0 ≤ t ≤ 0.5 で積分して求解します。プロットにグリッド線と凡例を追加します。

[tSol,ySol] = ode15i(F,[0 0.5],y0,yp0,opt);
plot(tSol,ySol(:,1:origVars),'LineWidth',2)

for k = 1:origVars
  S{k} = char(DAEvars(k));
end

legend(S,'Location','Best')
grid on

新しい変数を設定し、関数ハンドルと初期条件を再生成することで、異なるパラメーター値で系を解きます。

r に 2 を設定して、関数ハンドルと初期条件を再生成します。

r = 2;
F = @(t,Y,YP)f(t,Y,YP,g,m,r);

y0est = [r*sin(pi/6); -r*cos(pi/6); 0; 0; 0; 0; 0];
[y0,yp0] = decic(F,0,y0est,[],yp0est,[],opt);

新しいパラメーター値で系を解きます。

[tSol,y] = ode15i(F,[0 0.5],y0,yp0,opt);
plot(tSol,y(:,1:origVars),'LineWidth',2)

for k = 1:origVars
  S{k} = char(DAEvars(k));
end
legend(S,'Location','Best')
grid on

関連するトピック

• 半線形 DAE 系の求解
• 質量行列ソルバーを使用した DAE の求解

×

例を開く

この例の変更されたバージョンがあります。編集された方の例を開きますか?

いいえ、変更されたバージョンを上書きします。 はい