スティッフ ODE の求解
このページには、ode15s を使用してスティッフ常微分方程式を解く例が 2 つ含まれています。MATLAB® にはスティッフ ODE 用に設計されたソルバーが 4 つあります。
ode15sode23sode23tode23tb
スティッフなほとんどの問題には ode15s が最適です。ただし、許容誤差が粗い問題の場合は、ode23s、ode23t および ode23tb が効率的なことがあります。
スティッフ ODE とは
一部の ODE 問題では、解の曲線が滑らかな領域でも、ソルバーが取るステップ サイズが、積分区間に比べると過剰に小さいレベルまで強制的に設定されることがあります。このようにステップ サイズが非常に小さいと、短い時間区間を進む際に何百万もの評価が必要になることがあります。これはソルバーで積分が失敗する原因となる可能性があります。成功したとしても、処理にかかる時間が非常に長くなります。
ODE ソルバーでこのような動作の原因となる方程式は、"スティッフ" であるといわれます。スティッフ ODE での問題は、陽的ソルバー (ode45 など) が解を取得する際に処理速度が極度に遅くなることです。そのため、ode45 は、ode23、ode78、ode89、および ode113 と共に、"ノンスティッフ ソルバー" として分類されます。
スティッフ ODE 用に設計されたソルバーは "スティッフ ソルバー" と呼ばれ、通常はステップあたりの作業が多くなります。このメリットは、はるかに大きいステップをスティッフ ソルバーで取ることができるようになり、ノンスティッフ ソルバーよりも数値安定性が高くなることです。
ソルバー オプション
スティッフな問題の場合は、odeset を使用してヤコビ行列を指定することが特に重要です。スティッフ ソルバーでは、ヤコビ行列 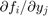 を使用して、積分が進む際の ODE の局所的動作を推定します。そのため、ヤコビ行列を指定 (つまり、大規模なスパース系に対して、そのスパース パターンを指定) することが効率性と信頼性の点から非常に重要になります。ヤコビアンに関する情報を指定するには、
を使用して、積分が進む際の ODE の局所的動作を推定します。そのため、ヤコビ行列を指定 (つまり、大規模なスパース系に対して、そのスパース パターンを指定) することが効率性と信頼性の点から非常に重要になります。ヤコビアンに関する情報を指定するには、odeset のオプション Jacobian、JPattern または Vectorized を使用します。ヤコビアンを指定しない場合、ソルバーは有限差分を使用してこの数値を推定します。
他のソルバー オプションの完全なリストについては、odesetを参照してください。
例: ファン デル ポールのスティッフな方程式
ファン デル ポールの方程式は次のように 2 次 ODE です。

ここで、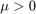 はスカラー パラメーターです。
はスカラー パラメーターです。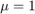 の場合、その結果得られる ODE 系はノンスティッフとなり、
の場合、その結果得られる ODE 系はノンスティッフとなり、ode45 を使用して容易に解を求められます。ただし、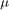 を 1,000 まで増やすと、この解は大きく変化し、時間スケールが長いと発振が起こります。初期値問題の解の近似はさらに難しくなります。特にこの問題はスティッフなので、
を 1,000 まで増やすと、この解は大きく変化し、時間スケールが長いと発振が起こります。初期値問題の解の近似はさらに難しくなります。特にこの問題はスティッフなので、ode45 のようなノンスティッフな問題に対応しているソルバーは非常に効率が悪く、実用に適しません。この問題には、代わりに ode15s などのスティッフ ソルバーを使用してください。
このファン デル ポールの方程式を 1 次 ODE 系として書き換えるには、代入  を行います。その結果得られる 1 次の ODE は、次のようになります。
を行います。その結果得られる 1 次の ODE は、次のようになります。
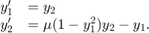
関数 vdp1000 では、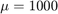 を使用してこのファン デル ポールの方程式を評価します。
を使用してこのファン デル ポールの方程式を評価します。
function dydt = vdp1000(t,y) %VDP1000 Evaluate the van der Pol ODEs for mu = 1000. % % See also ODE15S, ODE23S, ODE23T, ODE23TB. % Jacek Kierzenka and Lawrence F. Shampine % Copyright 1984-2014 The MathWorks, Inc. dydt = [y(2); 1000*(1-y(1)^2)*y(2)-y(1)];
関数 ode15s によって、初期条件ベクトル [2; 0] を使用して、時間区間 [0 3000] に対する解を求めます。スケーリング目的で、この解の 1 番目の要素のみをプロットします。
[t,y] = ode15s(@vdp1000,[0 3000],[2; 0]); plot(t,y(:,1),'-o'); title('Solution of van der Pol Equation, \mu = 1000'); xlabel('Time t'); ylabel('Solution y_1');

関数 vdpode でも同じ問題の解を求めることができますが、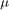 に対してユーザー指定の値を受け入れます。この方程式は
に対してユーザー指定の値を受け入れます。この方程式は 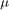 の値が大きくなるにつれ、徐々にスティッフになります。
の値が大きくなるにつれ、徐々にスティッフになります。
例: スパース Brusselator 連立方程式
古典的な Brusselator 連立方程式は大規模でスティッフなスパースになる可能性があります。Brusselator 方程式は化学反応の拡散作用をモデル化し、 、
、 、
、 および
および 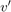 を使用した連立方程式で表されます。
を使用した連立方程式で表されます。
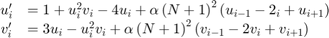
関数ファイル brussode では時間区間 [0,10] に対して 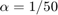 を使用し、この一連の方程式の解を求めます。初期条件は次のとおりです。
を使用し、この一連の方程式の解を求めます。初期条件は次のとおりです。
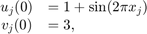
ここで、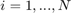 に対して
に対して 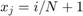 です。したがって、この方程式には
です。したがって、この方程式には  個の方程式がありますが、この方程式が
個の方程式がありますが、この方程式が 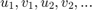 のように順序付けられている場合、ヤコビアン
のように順序付けられている場合、ヤコビアン 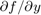 は定数幅 5 をもつ帯行列になります。この問題は、
は定数幅 5 をもつ帯行列になります。この問題は、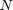 の値が大きくなるにつれ、徐々にスティッフになり、ヤコビアンも徐々にスパースになります。
の値が大きくなるにつれ、徐々にスティッフになり、ヤコビアンも徐々にスパースになります。
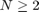 の場合、関数呼び出し
の場合、関数呼び出し brussode(N) では連立方程式の N に値を指定します。これはグリッド点の数に該当します。既定では、brussode は 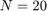 を使用します。
を使用します。
brussode にはサブ関数がいくつか含まれています。
入れ子関数
f(t,y)は Brusselator 問題の連立方程式をエンコードし、ベクトルを返します。ローカル関数
jpattern(N)は、ヤコビアン内の非ゼロの位置を示す 1 と 0 のスパース行列を返します。この行列はオプション構造体のJPatternフィールドに代入されます。ODE ソルバーはこのスパース パターンを使用して、ヤコビアンの数値をスパース行列として生成します。この問題でスパース パターンを指定すると、2N 行 2N 列のヤコビアンの生成に必要な関数評価回数が 2N からわずか 4 へと大幅に減ります。
function brussode(N) %BRUSSODE Stiff problem modelling a chemical reaction (the Brusselator). % The parameter N >= 2 is used to specify the number of grid points; the % resulting system consists of 2N equations. By default, N is 20. The % problem becomes increasingly stiff and increasingly sparse as N is % increased. The Jacobian for this problem is a sparse constant matrix % (banded with bandwidth 5). % % The property 'JPattern' is used to provide the solver with a sparse % matrix of 1's and 0's showing the locations of nonzeros in the Jacobian % df/dy. By default, the stiff solvers of the ODE Suite generate Jacobians % numerically as full matrices. However, when a sparsity pattern is % provided, the solver uses it to generate the Jacobian numerically as a % sparse matrix. Providing a sparsity pattern can significantly reduce the % number of function evaluations required to generate the Jacobian and can % accelerate integration. For the BRUSSODE problem, only 4 evaluations of % the function are needed to compute the 2N x 2N Jacobian matrix. % % Setting the 'Vectorized' property indicates the function f is % vectorized. % % E. Hairer and G. Wanner, Solving Ordinary Differential Equations II, % Stiff and Differential-Algebraic Problems, Springer-Verlag, Berlin, % 1991, pp. 5-8. % % See also ODE15S, ODE23S, ODE23T, ODE23TB, ODESET, FUNCTION_HANDLE. % Mark W. Reichelt and Lawrence F. Shampine, 8-30-94 % Copyright 1984-2014 The MathWorks, Inc. % Problem parameter, shared with the nested function. if nargin<1 N = 20; end tspan = [0; 10]; y0 = [1+sin((2*pi/(N+1))*(1:N)); repmat(3,1,N)]; options = odeset('Vectorized','on','JPattern',jpattern(N)); [t,y] = ode15s(@f,tspan,y0,options); u = y(:,1:2:end); x = (1:N)/(N+1); figure; surf(x,t,u); view(-40,30); xlabel('space'); ylabel('time'); zlabel('solution u'); title(['The Brusselator for N = ' num2str(N)]); % ------------------------------------------------------------------------- % Nested function -- N is provided by the outer function. % function dydt = f(t,y) % Derivative function c = 0.02 * (N+1)^2; dydt = zeros(2*N,size(y,2)); % preallocate dy/dt % Evaluate the 2 components of the function at one edge of the grid % (with edge conditions). i = 1; dydt(i,:) = 1 + y(i+1,:).*y(i,:).^2 - 4*y(i,:) + c*(1-2*y(i,:)+y(i+2,:)); dydt(i+1,:) = 3*y(i,:) - y(i+1,:).*y(i,:).^2 + c*(3-2*y(i+1,:)+y(i+3,:)); % Evaluate the 2 components of the function at all interior grid points. i = 3:2:2*N-3; dydt(i,:) = 1 + y(i+1,:).*y(i,:).^2 - 4*y(i,:) + ... c*(y(i-2,:)-2*y(i,:)+y(i+2,:)); dydt(i+1,:) = 3*y(i,:) - y(i+1,:).*y(i,:).^2 + ... c*(y(i-1,:)-2*y(i+1,:)+y(i+3,:)); % Evaluate the 2 components of the function at the other edge of the grid % (with edge conditions). i = 2*N-1; dydt(i,:) = 1 + y(i+1,:).*y(i,:).^2 - 4*y(i,:) + c*(y(i-2,:)-2*y(i,:)+1); dydt(i+1,:) = 3*y(i,:) - y(i+1,:).*y(i,:).^2 + c*(y(i-1,:)-2*y(i+1,:)+3); end % ------------------------------------------------------------------------- end % brussode % --------------------------------------------------------------------------- % Subfunction -- the sparsity pattern % function S = jpattern(N) % Jacobian sparsity pattern B = ones(2*N,5); B(2:2:2*N,2) = zeros(N,1); B(1:2:2*N-1,4) = zeros(N,1); S = spdiags(B,-2:2,2*N,2*N); end % ---------------------------------------------------------------------------
 の場合、Brusselator 連立方程式の解を求めるには、関数
の場合、Brusselator 連立方程式の解を求めるには、関数 brussode を実行します。
brussode

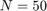 の場合、この連立方程式の解を求めるには、
の場合、この連立方程式の解を求めるには、brussode への入力を指定します。
brussode(50)

参考
ode15s | ode23s | ode23t | ode23tb