Main Content

ODE のイベント検出

このトピックでは、ソルバー関数 (ode45、ode15s など) を使用して ODE を解きながらイベントを検出する方法について説明します。

イベント検出とは

ODE 系の解を求める際に、求解を停止する適切なタイミングを判断することが困難な場合があります。積分区間の最終時間が、数値ではなく、特定のイベントによって定義されていることがあります。たとえば、木からリンゴが落ちる場合です。ODE ソルバーはリンゴが地面に落ちたら停止する必要がありますが、このイベントがいつ起こるかは事前にわからない可能性があります。同様に、求解が終了しないイベントを扱う問題もあります。たとえば、月が惑星を回る場合です。この場合、積分を早く停止しないことを推奨します。ただし、大きい方の天体を月が 1 周する各タイミングは検出します。

ODE の求解中に特定のイベントが発生するタイミングを検出するには、イベント関数を使用します。イベント関数ではユーザー指定の式を取り、その式がゼロに等しくなるタイミングのイベントを検出します。これらの関数はイベントを検出したときに ODE ソルバーに対して積分を停止するように合図を送ることもできます。

イベント関数の作成

イベント関数を指定するには、関数 odeset の 'Events' オプションを使用します。このイベント関数は次のような一般的な形式にしなければなりません。

[value,isterminal,direction] = myEventsFcn(t,y)

ode15i の場合、このイベント関数では yp に対して 3 番目の入力引数も受け入れなければなりません。

出力引数 value、isterminal および direction は、i 番目の要素が i 番目のイベントに対応するベクトルです。

  • value(i) は i 番目のイベントを記述する数式です。value(i) がゼロに等しくなると、イベントが発生します。

  • i 番目のイベント発生時に積分を終了する場合、isterminal(i) = 1 です。そうでない場合は、0 です。

  • すべての零点を検出する場合、direction(i) = 0 です (既定の設定)。+1 ではイベント関数が増加している零点のみが検出され、-1 ではイベント関数が減少している零点のみが検出されます。すべてのイベントに対して既定値 0 を使用する場合は、direction = [] を指定します。

木から落ちるリンゴの場合について再び考えます。落ちるものを表す ODE は次のようになります。

y''=−1+y' 2 ,

この初期条件は y(0)=1 および y'(0)=0 です。イベント関数を使用して y(t)=0 のタイミングを判断できますが、これはリンゴが地面に落ちるタイミングになります。この問題の場合、リンゴが地面に落ちるタイミングを検出するイベント関数は次のようになります。

function [position,isterminal,direction] = appleEventsFcn(t,y)
  position = y(1); % The value that we want to be zero
  isterminal = 1;  % Halt integration 
  direction = 0;   % The zero can be approached from either direction
end

イベント情報

イベント関数を指定する場合、3 つの追加出力引数を指定して ODE ソルバーを次のように呼び出します。

[t,y,te,ye,ie] = odeXY(odefun,tspan,y0,options)

このソルバーで返される 3 つの追加出力は、次のように検出イベントに対応します。

  • te は、イベントが発生した時刻の列ベクトルです。

  • ye には、te 内の各イベント時間における解の値が含まれます。

  • ie には、イベント関数によって返されるベクトルのインデックスが含まれます。値は、どのイベントをソルバーが検出したかを示します。

また、このソルバーは出力を 1 つのみ指定して呼び出すこともできます。

sol = odeXY(odefun,tspan,y0,options)

この場合、イベント情報は sol.te、sol.ye および sol.ie として構造体に保存されます。

制限

ODE ソルバーで採用されている根を求めるメカニズムがイベント関数と組み合わせて使用されると、次のような制約を受けます。

  • 積分の最初のステップで終了イベントが発生した場合、ソルバーはこのイベントを非終了イベントとして記録して、積分を続行します。

  • 最初のステップで複数の終了イベントが発生した場合、最初のイベントのみが記録され、ソルバーは積分を続行します。

  • 零点はステップ間で符号が切り替わることにより判別されます。したがって、ステップ間での切り替えが偶数回発生する関数の零点は識別されないことがあります。

ソルバーのステップでイベントが検出されない場合は、精度を高めるために RelTol および AbsTol の値を小さくしてみてください。あるいは、MaxStep を設定して、ステップ サイズの上限を指定します。tspan を調整しても、ソルバーが取るステップは変わりません。

簡単なイベントの検出問題: 跳ねるボール

スクリプトを開く

この例では、ODE ソルバーと併用する簡単なイベント関数の作成方法を説明します。サンプル ファイル ballode は、跳ねるボールの運動をモデル化します。このイベント関数はボールが跳ねるたびに積分を停止し、新しい初期条件を使用して積分を再開します。ボールが跳ねている間、積分の停止と再開が数回行われます。

跳ねるボールの方程式は次のように表せます。

$$\begin{array}{cl} y'_1 &= y_2\\ y'_2 &= -9.8 . \end{array}$$

跳ねるボールの高さ 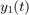$y_1(t)$ が低くなってゼロに等しくなると、ボールが跳ねます。この動作をコード化したイベント関数は次のようになります。

function [value,isterminal,direction] = bounceEvents(t,y)
value = y(1);     % Detect height = 0
isterminal = 1;   % Stop the integration
direction = -1;   % Negative direction only

ballode と入力すると、この例が実行され、跳ねるボールをシミュレートするイベント関数の使用方法を確認できます。

ballode

高度なイベント検出問題: 制約付き三体問題

スクリプトを開く

この例では、イベント関数の方向要素を使用する方法を説明します。サンプル ファイル orbitode では、1 つの物体が、それよりもはるかに大きい 2 つの物体を周回する制約付き三体問題をシミュレートします。このイベント関数では、周回する物体が軌道上で最も近付く点と最も離れる点を特定します。イベント関数の値は軌道の最近点と最遠点で同じになるため、ゼロクロッシングの方向によってそれらを区別します。

制約付き三体問題の方程式は次のようになります。

$$\begin{array}{cl} y'_1 &= y_3\\ y'_2 &= y_4 \\ y'_3 &= 2y_4 + y_1 -
\frac{\mu^* (y_1 + \mu)}{r_1^3} - \frac{\mu(y_1 - \mu^*}{r_2^3}\\ y'_4 &=
-2y_3 + y_2 - \frac{\mu^* y_2}{r_1^3} - \frac{\mu y_2}{r_2^3},
\end{array}$$

ここで以下のようになります。

$$\begin{array}{cl} \mu &= 1/82.45\\ \mu^* &= 1-\mu\\ r_1 &=
\sqrt{(y_1+\mu)^2+y_2^2}\\ r_2 &= \sqrt{(y_1-\mu^*)^2 +
y_2^2}.\end{array}$$

最初の 2 つの解要素は無限小の質量をもつ質点の座標系で、一方の解要素を、他方の解要素に対してプロットしたものが、その質点の軌跡になります。

orbitode.m で入れ子になっているイベント関数は 2 つのイベントを探索します。一方のイベントでは開始点から最も遠い点を見つけます。もう一方のイベントでは宇宙船が開始点に戻る点を見つけます。積分器に使われるステップ サイズはイベントの位置には依存しませんが、イベント位置自体は正確に検出されます。この例では、ゼロクロッシングの方向を決める機能が重要な役割を果たします。開始点への折り返し点と開始点からの最大距離の点は同じイベント値になりますが、交差の方向を使用してそれらを区別します。この動作をコード化したイベント関数は次のようになります。

function [value,isterminal,direction] = orbitEvents(t,y)
% dDSQdt is the derivative of the equation for current distance. Local
% minimum/maximum occurs when this value is zero.
dDSQdt = 2 * ((y(1:2)-y0(1:2))' * y(3:4)); 
value = [dDSQdt; dDSQdt];  
isterminal = [1;  0];         % stop at local minimum
direction  = [1; -1];         % [local minimum, local maximum]
end

この例を実行するには、orbitode と入力します。

orbitode

This is an example of event location where the ability to
specify the direction of the zero crossing is critical.  Both
the point of return to the initial point and the point of
maximum distance have the same event function value, and the
direction of the crossing is used to distinguish them.

Calling ODE45 with event functions active...

Note that the step sizes used by the integrator are NOT
determined by the location of the events, and the events are
still located accurately.

参考

|

関連するトピック