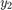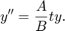ode113

ノンスティッフ微分方程式の求解 — 可変次数法

ページ内をすべて折りたたむ

構文

[t,y] = ode113(odefun,tspan,y0)
[t,y] = ode113(odefun,tspan,y0,options)
[t,y,te,ye,ie] = ode113(odefun,tspan,y0,options)
sol = ode113(___)

説明

[t,y] = ode113(odefun,tspan,y0) は、tspan = [t0 tf] のときに、初期条件 y0 を使用して、連立微分方程式 y'=f(t,y) を t0 から tf まで積分します。解の配列 y の各行は、列ベクトル t に返される値に対応します。

すべての MATLAB® ODE ソルバーは、y'=f(t,y) の形式の連立方程式、あるいは質量行列 M(t,y)y'=f(t,y) を含む問題を解くことができます。すべてのソルバーは類似した構文を使用します。ode23s ソルバーは、質量行列が定数である場合にのみ、これを含む問題を解くことができます。ode15s および ode23t は、特異質量行列をもつ方程式、つまり微分代数方程式 (DAE) を解くことができます。odeset の Mass オプションを使用して質量行列を指定します。

例

[t,y] = ode113(odefun,tspan,y0,options) は options (関数 odeset を使用して作成された引数) で定義された積分設定も使用します。たとえば、AbsTol オプションおよび RelTol オプションを使用して絶対許容誤差と相対許容誤差を指定したり、Mass オプションを使用して質量行列を指定することができます。

例

[t,y,te,ye,ie] = ode113(odefun,tspan,y0,options) はさらに、(t,y) の関数 (イベント関数) がゼロになる点を求めます。出力の te はイベント時点、ye はイベント時点における解、ie はトリガーされたイベントのインデックスです。

各関数に対して、ゼロで積分を終了するかどうかと、ゼロクロッシングの方向を考慮するかどうかを指定します。これを行うには、myEventFcn や @myEventFcn などの関数に 'Events' プロパティを設定し、対応する関数 [value,isterminal,direction] = myEventFcn(t,y) を作成します。詳細については、ODE のイベント検出を参照してください。

sol = ode113(___) は、区間 [t0 tf] の任意の点で解を計算する関数 deval で使用できる構造体を返します。前述の構文にある任意の入力引数の組み合わせが使用できます。

例

すべて折りたたむ

ライブ スクリプトを開く

単一解要素をもつシンプルな ODE は、ソルバーの呼び出し内に無名関数として指定できます。この無名関数は、2 つの入力 (t,y) を受け入れなければなりません (いずれかの入力が関数で使用されない場合でも)。

次の ODE を解きます。

y′=2t.

時間区間 [0 5] および初期条件 y0 = 0 を指定します。

tspan = [0 5];
y0 = 0;
[t,y] = ode113(@(t,y) 2*t, tspan, y0);

解をプロットします。

plot(t,y,'-o')

Figure contains an axes object. The axes object contains an object of type line.

スクリプトを開く

ファン デル ポールの方程式は次のように 2 次 ODE です。

$$y''_1 - \mu \left( 1 - y_1^2\right) y'_1+y_1=0,$$

ここで、$\mu > 0$ はスカラー パラメーターです。代入 $y'_1 = y_2$ を行い、この方程式を 1 次 ODE 系として書き換えます。その結果得られる 1 次の ODE は、次のようになります。

$$
\begin{array}{cl}
y'_1 &= y_2\\
y'_2 &= \mu (1-y_1^2) y_2 - y_1.\end{array}
$$

関数ファイル vdp1.m は、$\mu = 1$ を使用するファン デル ポールの方程式を表します。変数 $y_1$ と変数 $y_2$ は、2 要素ベクトル dydt のエントリ y(1) および y(2) です。

function dydt = vdp1(t,y)
%VDP1  Evaluate the van der Pol ODEs for mu = 1
%
%   See also ODE113, ODE23, ODE45.

%   Jacek Kierzenka and Lawrence F. Shampine
%   Copyright 1984-2014 The MathWorks, Inc.

dydt = [y(2); (1-y(1)^2)*y(2)-y(1)];

関数 ode113 を使用し、初期値 [2 0] を指定して、時間区間 [0 20] でこの ODE の解を求めます。その結果、出力として時間の列ベクトル t と解の配列 y が得られます。y の各行は、t の対応する行に返される時刻と対応します。y の 1 列目は $y_1$ に対応し、2 列目は $y_2$ に対応します。

[t,y] = ode113(@vdp1,[0 20],[2; 0]);

$y_1$ および $y_2$ の解を t に対してプロットします。

plot(t,y(:,1),'-o',t,y(:,2),'-o')
title('Solution of van der Pol Equation (\mu = 1) with ODE113');
xlabel('Time t');
ylabel('Solution y');
legend('y_1','y_2')

スクリプトを開く

ode113 は、2 つの入力引数 t と y を使用する関数にのみ使用できます。しかし、関数の外部で定義した追加のパラメーターを、関数ハンドルを指定するタイミングで渡すことができます。

次の ODE を解きます。

$$y'' = \frac{A}{B} t y.$$

この方程式を連立 1 階方程式として書き直すと次のようになります。

$$\begin{array}{cl} y'_1 &= y_2\\ y'_2 &= \frac{A}{B} t y_1.
\end{array}$$

odefcn.m はこの連立方程式を 4 つの入力引数 (t、y、A、B) を受け入れる関数として表します。

function dydt = odefcn(t,y,A,B)
dydt = zeros(2,1);
dydt(1) = y(2);
dydt(2) = (A/B)*t.*y(1);

ode113 を使用して ODE を解きます。事前定義された A と B の値を odefcn に渡す関数ハンドルを指定します。

A = 1;
B = 2;
tspan = [0 5];
y0 = [0 0.01];
[t,y] = ode113(@(t,y) odefcn(t,y,A,B), tspan, y0);

結果をプロットします。

plot(t,y(:,1),'-o',t,y(:,2),'-.')

スクリプトを開く

ode45 よりも ode113、ode78、および ode89 のソルバーの方が、厳密な許容誤差をもつ問題を解く場合に優れています。ode113 が優れている一般的な状況は、滑らかな解の曲線と高い精度が要求される軌道力学の問題です。

二体問題では、共通の平面上を周回する、相互に作用する 2 つの質量 m1 と m2 について考えます。この例では、一方の質量が他方の質量よりもはるかに大きいものとします。質量の大きい物体を原点に置くと、運動方程式は次のようになります。

$$\begin{array}{cl} x'' &= -x/r^3\\ y'' &= -y/r^3,\end{array}$$

ここで、

$$r = \sqrt{x^2+y^2}.$$

この問題を解くには、まず代入を行って 4 つの 1 次 ODE からなる方程式に変換します。

$$\begin{array}{cl} y_1 &= x\\ y_2 &= x'\\ y_3 &= y\\ y_4 &=
y'.\end{array}$$

代入により連立 1 階方程式が生成されます。

$$\begin{array}{cl} y'_1 &= y_2\\ y'_2 &= -y_1/r^3\\ y'_3 &= y_4 \\ y'_4
&= -y_3/r^3.\end{array}$$

関数 twobodyode は二体問題の連立方程式をコード化したものです。

function dy = twobodyode(t,y)
% Two body problem with one mass much larger than the other.
r = sqrt(y(1)^2 + y(3)^2);
dy = [y(2); 
    -y(1)/r^3;
    y(4);
    -y(3)/r^3];

twobodyode.m を作業ディレクトリに保存してから、ode113 を使用して ODE を解きます。RelTol には 1e-13、AbsTol には 1e-14 の厳密な許容誤差を指定します。

opts = odeset('Reltol',1e-13,'AbsTol',1e-14,'Stats','on');
tspan = [0 10*pi];
y0 = [2 0 0 0.5];

[t,y] = ode113(@twobodyode, tspan, y0, opts);
plot(t,y)
legend('x','x''','y','y''','Location','SouthEast')
title('Position and Velocity Components')

924 successful steps
4 failed attempts
1853 function evaluations


figure
plot(y(:,1),y(:,3),'-o',0,0,'ro')
axis equal
title('Orbit of Smaller Mass')

ode113 ソルバーは、ode45 よりも少ない関数評価と短い時間で解を得ることができます。

入力引数

すべて折りたたむ

解を求める関数。積分する関数を定義する関数ハンドルとして指定します。

スカラー t および列ベクトル y をとる関数 dydt = odefun(t,y) は、データ型が single または double で f(t,y) に対応する列ベクトル dydt を返さなければなりません。odefun は、t と y のいずれかの引数が関数で使用されない場合でも、両方の入力引数を受け入れなければなりません。

たとえば、y'=5y−3 を解くには、次の関数を使用します。

function dydt = odefun(t,y)
dydt = 5*y-3;
end

連立方程式の場合、odefun の出力はベクトルです。ベクトルの各要素は 1 つの方程式の右辺の計算値です。たとえば、次の 2 つを含む連立方程式について考えます。

y'1=y1+2y2y'2=3y1+2y2

各タイム ステップで各方程式の右辺の値を計算する関数は以下のとおりです。

function dydt = odefun(t,y)
dydt = zeros(2,1);
dydt(1) = y(1)+2*y(2);
dydt(2) = 3*y(1)+2*y(2);
end

関数 odefun に追加パラメーターを指定する方法の詳細については、関数のパラメーター化を参照してください。

例: @myFcn

データ型: function_handle

積分区間。ベクトルとして指定します。少なくとも、tspan は開始時点と終了時点を指定する 2 要素ベクトル [t0 tf] でなければなりません。t0 と tf の間の特定時点における解を取得するには、[t0,t1,t2,...,tf] の形式の長いベクトルを使用します。tspan の要素は、単調増加または単調減少でなければなりません。

ソルバーは開始時点 tspan(1) で y0 によって指定される初期条件を設定し、tspan(1) から tspan(end) まで積分します。

  • tspan に 2 つの要素がある場合 ([t0 tf])、ソルバーは区間内の個々の内部積分ステップで計算した解を返します。

  • tspan に 2 つを超える要素がある場合 ([t0,t1,t2,...,tf])、ソルバーは指定された各点で計算した解を返します。ただし、ソルバーは tspan で指定された各点に正確にステップするわけではありません。代わりに、ソルバーは独自の内部ステップを使用して解を計算し、tspan 内の要求された点で解を評価します。指定された点で出力された解の精度の次数は、各内部ステップで計算された解と同じです。

    中間点をいくつか指定しても計算効率にほとんど影響しませんが、大規模な方程式の場合はメモリ管理に影響を及ぼす可能性があります。

ソルバーは tspan の値を使用して InitialStep と MaxStep に適した値を計算します。

  • tspan に複数の中間点が含まれる場合 ([t0,t1,t2,...,tf])、指定した点は問題のスケールの目安となり、これはソルバーが使用する InitialStep の値に影響することがあります。そのため、ソルバーで得られる解は、tspan を 2 要素ベクトルとして指定するか、中間点を含むベクトルとして指定するかによって異なる場合があります。

  • tspan の最初と最後の値は、最大ステップ サイズ MaxStep の計算に使用されます。そのため、tspan の最初または最後の値を変更すると、ソルバーが別のステップ シーケンスを使用する可能性があり、そのため解が変わることがあります。

例: [1 10]

例: [1 3 5 7 9 10]

データ型: single | double

初期条件。ベクトルとして指定します。odefun に定義された各方程式の初期条件を y0 に含めるために、y0 は odefun のベクトル出力と同じ長さでなければなりません。

データ型: single | double

オプション構造体。構造体配列として指定します。options 構造体の作成または変更には、関数 odeset を使用します。各 ODE ソルバーと互換性のあるオプションの一覧については、ODE オプションの概要を参照してください。

例: options = odeset('RelTol',1e-5,'Stats','on','OutputFcn',@odeplot) は、相対許容誤差 1e-5 を指定し、ソルバー統計の表示をオンにして、解の計算時に解をプロットする出力関数 @odeplot を指定します。

データ型: struct

出力引数

すべて折りたたむ

評価点。列ベクトルとして返されます。

  • tspan に 2 つの要素がある場合 ([t0 tf])、t には積分の実行に使用される内部評価点が含まれます。

  • tspan に 2 つより多い要素が含まれる場合、t は tspan と同じです。

解。配列として返されます。y の各行は、t の対応する行に返される値での解です。

イベント時点。列ベクトルとして返されます。te のイベント時点は ye に返された解に対応し、ie は発生したイベントを指定します。

イベント時点での解。配列として返されます。te のイベント時点は ye に返された解に対応し、ie は発生したイベントを指定します。

トリガーされるイベント関数のインデックス。列ベクトルとして返されます。te のイベント時点は ye に返された解に対応し、ie は発生したイベントを指定します。

評価対象の構造体。構造体配列として返されます。この構造体を関数 deval と共に使用して区間 [t0 tf] の任意の点で解を評価します。構造体配列 sol は、常に以下のフィールドを含みます。

構造体フィールド説明

sol.x

ソルバーによって選択されたステップの行ベクトル。

sol.y

解。各列の sol.y(:,i) には、時点 sol.x(i) での解が含まれます。

sol.solver

ソルバー名。

さらに、odeset の Events オプションを指定してイベントが検出された場合、sol は以下のフィールドも含みます。

構造体フィールド説明

sol.xe

イベントが発生した点。sol.xe(end) には、終了イベントの厳密な点 (存在する場合) が含まれます。

sol.ye

sol.xe のイベントに対応する解。

sol.ie

Events オプションに指定された関数により返されるベクトルのインデックス。値は、どのイベントをソルバーが検出したかを示します。

アルゴリズム

ode113 は 1 次 ～ 13 次の可変ステップ、可変次数 (VSVO) の Adams-Bashforth-Moulton PECE 法ソルバーです。使用する最高次数は 12 のようですが、誤差推定の作成には 13 次の式が使用されます。また、この関数はローカル外挿を実行して 13 次で積分を進めます。

許容誤差が厳しい場合や ODE 関数の評価に特に時間のかかる場合、ode113 の方が ode45 より効率的なことがあります。ode113 は複数ステップ ソルバーです。つまり、通常は現時点の解を計算するために、それより前の複数時点の解が必要です。[1] [2]

参照

[1] Shampine, L. F. and M. K. Gordon, Computer Solution of Ordinary Differential Equations: the Initial Value Problem, W. H. Freeman, San Francisco, 1975.

[2] Shampine, L. F. and M. W. Reichelt, “The MATLAB ODE Suite,” SIAM Journal on Scientific Computing, Vol. 18, 1997, pp. 1–22.

バージョン履歴

R2006a より前に導入

参考

| | | | | | |

トピック