ノンスティッフ ODE の求解

このページには、ode45 を使用してノンスティッフ常微分方程式を解く例が 2 つ含まれています。MATLAB® にはノンスティッフ ODE のソルバーが複数あります。

ode45
ode23
ode78
ode89
ode113

ノンスティッフなほとんどの問題には ode45 が最適です。ただし、許容誤差が多少粗い問題や中程度のスティッフがある問題には、ode23 を推奨します。同様に、より厳しい許容誤差が設定された問題や ODE 関数の評価に計算量が多くなる場合では、ode45 よりも ode113 の方が効率的なことがあります。ode78 および ode89 は高次のソルバーで、安定性のために精度が重要な長い積分に優れています。

ノンスティッフソルバーで問題の求解に時間がかかる場合や積分での失敗が続く場合は、その問題は "スティッフ" な可能性があります。詳細については、スティッフ ODE の求解を参照してください。

例: ファンデルポールのノンスティッフな方程式

ファンデルポールの方程式は次のように 2 次 ODE です。

$y''_1 - \mu \left( 1 - y_1^2\right) y'_1+y_1=0,$

ここで、 $\mu > 0$ はスカラーパラメーターです。代入 $y'_1 = y_2$ を行って、この方程式を 1 次 ODE 系として書き換えます。その結果得られる 1 次の ODE は、次のようになります。

$
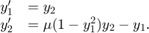
\begin{array}{cl}
y'_1 &= y_2\\
y'_2 &= \mu (1-y_1^2) y_2 - y_1.\end{array}
$

ODE 系は ODE ソルバーで使用できるように関数ファイル内にコード化しなければなりません。ODE 関数の汎用関数シグネチャは次のとおりです。

  dydt = odefun(t,y)

つまり、この関数では t および y の両方を入力として受け入れなければなりません。これは、t が計算で使用されない場合でも同様です。

関数ファイル vdp1.m では、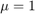 $\mu = 1$ を使用してファンデルポールの方程式をコード化しています。変数 $y_1$ および $y_2$ は、y(1) と y(2) で表され、2 要素の列ベクトル dydt には、 $y'_1$ と $y'_2$ の式が含まれます。

function dydt = vdp1(t,y)
%VDP1  Evaluate the van der Pol ODEs for mu = 1
%
%   See also ODE113, ODE23, ODE45.

%   Jacek Kierzenka and Lawrence F. Shampine
%   Copyright 1984-2014 The MathWorks, Inc.

dydt = [y(2); (1-y(1)^2)*y(2)-y(1)];

関数 ode45 を使用し、初期値 [2 0] を指定して、時間区間 [0 20] でこの ODE の解を求めます。この出力として時間点の列ベクトル t と解の配列 y が得られます。y の各行は、t の対応する行に返される時刻と対応します。y の 1 列目は $y_1$ に対応し、2 列目は $y_2$ に対応します。

[t,y] = ode45(@vdp1,[0 20],[2; 0]);

$y_1$ および $y_2$ の解を t に対してプロットします。

plot(t,y(:,1),'-o',t,y(:,2),'-o')
title('Solution of van der Pol Equation (\mu = 1) using ODE45');
xlabel('Time t');
ylabel('Solution y');
legend('y_1','y_2')

関数 vdpode でも同じ問題の解を求めることができますが、 $\mu$ に対してユーザー指定の値を受け入れます。 $\mu$ の値が大きくなるにつれ、ファンデルポールの方程式はスティッフになります。たとえば、値 $\mu = 1000$ を使用する場合は、ode15s のようなスティッフソルバーを使用してこの系を解く必要があります。

例: ノンスティッフオイラー方程式

外力のない剛体のオイラー方程式は、ノンスティッフな問題を対象とする ODE ソルバーの標準テスト問題です。

方程式は次のとおりです。

$\begin{array}{cl} y'_1 &= y_2y_3 \\ y'_2 &= -y_1y_3 \\ y'_3 &=
-0.51y_1y_2. \end{array}$

関数ファイル rigidode では、 $y_1$ 、 $y_2$ および $y_3$ の初期値に対応する初期条件ベクトル [0; 1; 1] を使用して、この 1 次の方程式系を時間区間 [0 12] に対して定義し、その解を求めています。ローカル関数 f(t,y) によって方程式系をエンコードしています。

rigidode は出力引数なしで ode45 を呼び出しているため、ソルバーは既定の出力関数 odeplot を使用して、各ステップの後に解の点を自動的にプロットします。

function rigidode
%RIGIDODE  Euler equations of a rigid body without external forces.
%   A standard test problem for non-stiff solvers proposed by Krogh.  The
%   analytical solutions are Jacobian elliptic functions, accessible in
%   MATLAB.  The interval here is about 1.5 periods; it is that for which
%   solutions are plotted on p. 243 of Shampine and Gordon.
%
%   L. F. Shampine and M. K. Gordon, Computer Solution of Ordinary
%   Differential Equations, W.H. Freeman & Co., 1975.
%
%   See also ODE45, ODE23, ODE113, FUNCTION_HANDLE.

%   Mark W. Reichelt and Lawrence F. Shampine, 3-23-94, 4-19-94
%   Copyright 1984-2014 The MathWorks, Inc.

tspan = [0 12];
y0 = [0; 1; 1];

% solve the problem using ODE45
figure;
ode45(@f,tspan,y0);

% --------------------------------------------------------------------------

function dydt = f(t,y)
dydt = [    y(2)*y(3)
   -y(1)*y(3)
   -0.51*y(1)*y(2) ];

ノンスティッフオイラー方程式の解を求めるには、関数 rigidode を呼び出します。

rigidode
title('Solution of Rigid Body w/o External Forces using ODE45')
legend('y_1','y_2','y_3','Location','Best')

参考

ode45 | ode23 | ode78 | ode89 | ode113

ノンスティッフ ODE の求解

例: ファン デル ポールのノンスティッフな方程式

例: ノンスティッフ オイラー方程式

参考

関連するトピック

例: ファンデルポールのノンスティッフな方程式

例: ノンスティッフオイラー方程式