interp1
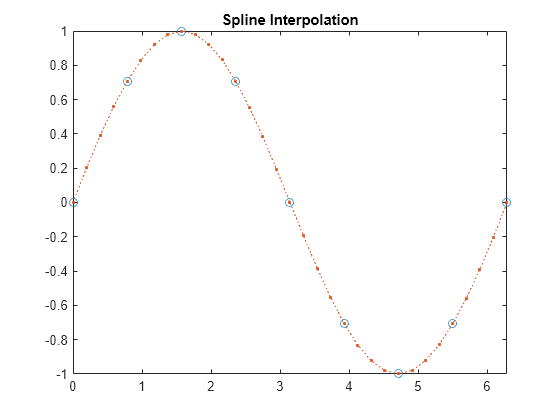
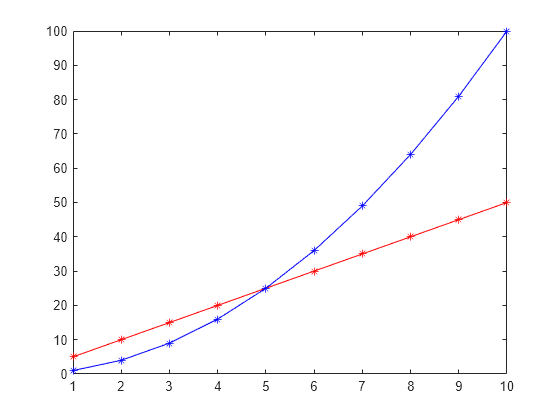
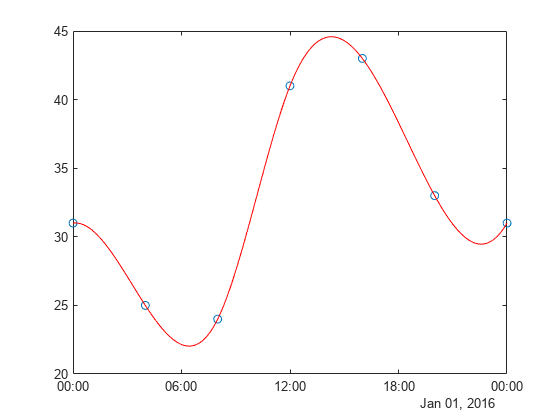
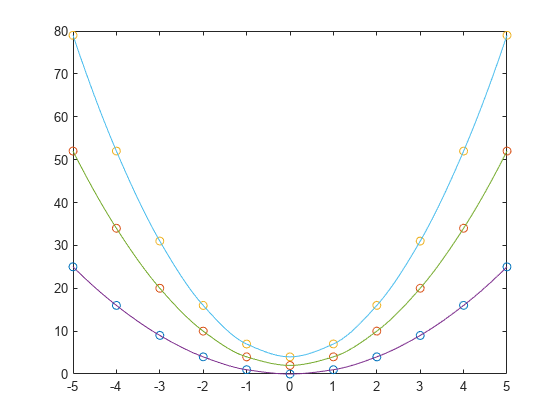
1 次データ内挿 (テーブル ルックアップ)
構文
説明
vq = interp1(v,xq,method,extrapolation)
pp = interp1(x,v,method,'pp')method アルゴリズムを使用して、v (x) の区分的多項式を返します。
メモ
この構文は推奨されません。代わりに griddedInterpolant を使用してください。
例
サンプル点 x と、対応するサンプル値 v を定義します。
x = 0:pi/4:2*pi; v = sin(x);
x を含む範囲内でより細かくサンプリングを行うためのクエリ点を定義します。
xq = 0:pi/16:2*pi;
クエリ点に関数を内挿し、結果をプロットします。
figure vq1 = interp1(x,v,xq); plot(x,v,'o',xq,vq1,':.'); xlim([0 2*pi]); title('(Default) Linear Interpolation');
'spline' メソッドを使用して、同じ点で v を評価します。
figure vq2 = interp1(x,v,xq,'spline'); plot(x,v,'o',xq,vq2,':.'); xlim([0 2*pi]); title('Spline Interpolation');
一連の関数値を定義します。
v = [0 1.41 2 1.41 0 -1.41 -2 -1.41 0];
既定の点 1:9 の間に位置する、一連のクエリ点を定義します。この場合、v は 9 の値を含むため、既定の点は 1:9 です。
xq = 1.5:8.5;
xq で v を評価します。
vq = interp1(v,xq);
結果をプロットします。
figure plot((1:9),v,'o',xq,vq,'*'); legend('v','vq');
一連のサンプル点を定義します。
x = 1:10;
サンプル点における関数 の値を定義します。
v = (5*x)+(x.^2*1i);
x を含む範囲内でより細かくサンプリングを行うためのクエリ点を定義します。
xq = 1:0.25:10;
クエリ点で v を内挿します。
vq = interp1(x,v,xq);
結果の実数部を赤でプロットし、虚数部を青でプロットします。
figure plot(x,real(v),'*r',xq,real(vq),'-r'); hold on plot(x,imag(v),'*b',xq,imag(vq),'-b');
タイムスタンプ付きデータ点を内挿します。
4 時間ごとに測定する温度測定値を含むデータ セットを考えてみましょう。1 日分のデータに相当する table を作成し、データをプロットします。
x = (datetime(2016,1,1):hours(4):datetime(2016,1,2))'; x.Format = 'MMM dd, HH:mm'; T = [31 25 24 41 43 33 31]'; WeatherData = table(x,T,'VariableNames',{'Time','Temperature'})
WeatherData=7×2 table
Time Temperature
_____________ ___________
Jan 01, 00:00 31
Jan 01, 04:00 25
Jan 01, 08:00 24
Jan 01, 12:00 41
Jan 01, 16:00 43
Jan 01, 20:00 33
Jan 02, 00:00 31
plot(WeatherData.Time, WeatherData.Temperature, 'o')
データ セットを内挿して、この日の 1 分ごとの温度測定値を予測します。データは周期的なので、'spline' 内挿法を使用できます。
xq = (datetime(2016,1,1):minutes(1):datetime(2016,1,2))';
V = interp1(WeatherData.Time, WeatherData.Temperature, xq, 'spline');内挿点をプロットします。
hold on plot(xq,V,'r')
サンプル点 x と、対応するサンプル値 v を定義します。
x = [1 2 3 4 5]; v = [12 16 31 10 6];
x の領域を越えるクエリ点 xq を指定します。
xq = [0 0.5 1.5 5.5 6];
'pchip' メソッドを使用して、xq で v を評価します。
vq1 = interp1(x,v,xq,'pchip')vq1 = 1×5
19.3684 13.6316 13.2105 7.4800 12.5600
次に 'linear' メソッドを使用して、xq で v を評価します。
vq2 = interp1(x,v,xq,'linear')vq2 = 1×5
NaN NaN 14 NaN NaN
ここで 'linear' メソッドを 'extrap' オプションで使用します。
vq3 = interp1(x,v,xq,'linear','extrap')
vq3 = 1×5
8 10 14 4 2
既定では 'pchip' は外挿を実行しますが、'linear' は外挿を行いません。
サンプル点 x と、対応するサンプル値 v を定義します。
x = [-3 -2 -1 0 1 2 3]; v = 3*x.^2;
x の領域を越えるクエリ点 xq を指定します。
xq = [-4 -2.5 -0.5 0.5 2.5 4];
ここで 'pchip' メソッドを使用して、xq で v を評価し、x の領域の外側の任意の値を、値 27 に割り当てます。
vq = interp1(x,v,xq,'pchip',27)vq = 1×6
27.0000 18.6562 0.9375 0.9375 18.6562 27.0000
サンプル点を定義します。
x = (-5:5)';
x で定義された点で、3 つの異なる放物線関数をサンプリングします。
v1 = x.^2; v2 = 2*x.^2 + 2; v3 = 3*x.^2 + 4;
列がベクトル v1、v2 および v3 で構成される行列 v を作成します。
v = [v1 v2 v3];
x を含む範囲内でより細かくサンプリングを行うための一連のクエリ点 xq を定義します。
xq = -5:0.1:5;
xq で 3 つの関数すべてを評価し、結果をプロットします。
vq = interp1(x,v,xq,'pchip'); figure plot(x,v,'o',xq,vq); h = gca; h.XTick = -5:5;
プロット内の円は v を表し、実線は vq を表します。
入力引数
出力引数
詳細
1 次元内挿の Akima アルゴリズム ([1] および [2] を参照) は、3 次内挿を実行して、連続 1 次微分 (C1) で区分的多項式を生成します。このアルゴリズムは傾きを保持し、変動の少ない領域のうねりを防ぎます。同一平面上に 3 つ以上の連続する点があり、このアルゴリズムにより直線で接続されている場合、常に変動の少ない領域が発生します。2 つのデータ点間の領域をフラットにするために、これらの 2 点間に追加のデータを挿入します。
傾きが異なる 2 つの変動の少ない領域が一致する場合、元の Akima アルゴリズムに修正を加えると、傾きが 0 に近い側に多くの重みが割り当てられます。この変更によって、より直観的な水平に近い側が優先され、オーバーシュートが回避されます (元の Akima アルゴリズムでは両側の点に同等の重みが割り当てられるため、うねりは均等に分割されます)。
一方のスプライン アルゴリズムは、3 次内挿を実行して、連続 2 次微分 (C2) で区分的多項式を生成します。結果は通常の多項式内挿と同等ですが、度数の高いデータ点間の大きな発振に影響されにくくなります。ただし、この方法では、データ点間のオーバーシュートや発振の影響を受ける場合があります。
spline アルゴリズムと比べると、Akima アルゴリズムでは生成されるうねりが少ないため、変動の少ない領域の間で急激に変化する場合への適用に適しています。この違いを、複数の変動の少ない領域を接続するテスト データを使用して以下に示します。
参照
[1] Akima, Hiroshi. "A new method of interpolation and smooth curve fitting based on local procedures." Journal of the ACM (JACM) , 17.4, 1970, pp. 589-602.
[2] Akima, Hiroshi. "A method of bivariate interpolation and smooth surface fitting based on local procedures." Communications of the ACM , 17.1, 1974, pp. 18-20.
