gammainc
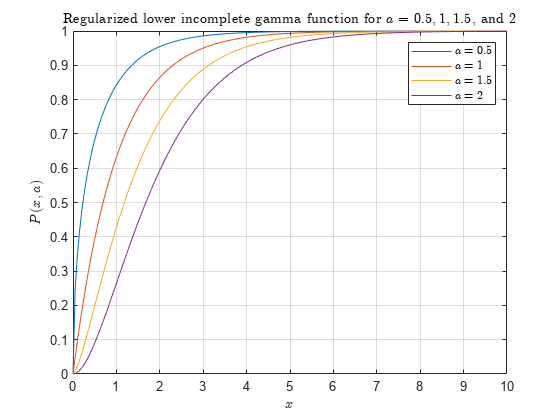
Regularized incomplete gamma function
Description
Y = gammainc(X,A)X and
A. Both X and A must be real,
and A must be nonnegative.
Examples
Input Arguments
Limitations
When x is negative, the regularized incomplete gamma function can be inaccurate for abs(x) > a+1.
More About
Tips
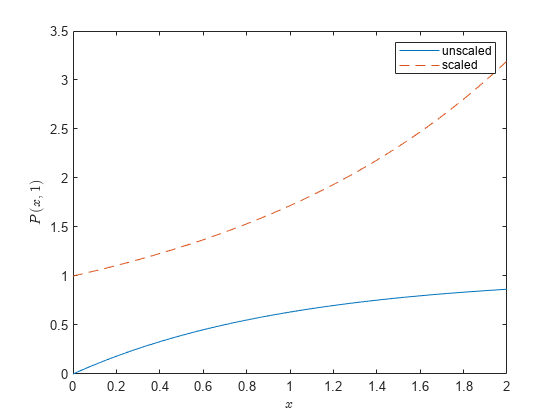
When the regularized upper incomplete gamma function is close to 0, specifying the
'upper'option to calculate the function is more accurate than subtracting the regularized lower incomplete gamma function from 1.
References
[1] Olver, F. W. J., A. B. Olde Daalhuis, D. W. Lozier, B. I. Schneider, R. F. Boisvert, C. W. Clark, B. R. Miller, and B. V. Saunders, eds., Chapter 8. Incomplete Gamma and Related Functions, NIST Digital Library of Mathematical Functions, Release 1.0.22, Mar. 15, 2018.
Extended Capabilities
Version History
Introduced before R2006a
See Also
gamma | gammaincinv | gammaln | psi