Main Content

このページの翻訳は最新ではありません。ここをクリックして、英語の最新版を参照してください。

csc

入力角度 (ラジアン単位) の余割

ページ内をすべて折りたたむ

構文

Y = csc(X)

説明

例

Y = csc(X) は、X の要素の余割を返します。関数 csc は、配列の要素単位で演算を行います。この関数は、実数入力と複素数入力の両方を受け入れます。

  • X が実数値の場合、csc(X) は区間 [-∞, -1] および [1, ∞] 内の実数値を返す。

  • X が複素数値の場合、csc(X) は複素数値を返す。

例

すべて折りたたむ

ライブ スクリプトを開く

以下に示すように、定義域 -π<x<0 および 0<x<π で余割関数をプロットします。

x1 = -pi+0.01:0.01:-0.01; 
x2 = 0.01:0.01:pi-0.01;
plot(x1,csc(x1),x2,csc(x2)), grid on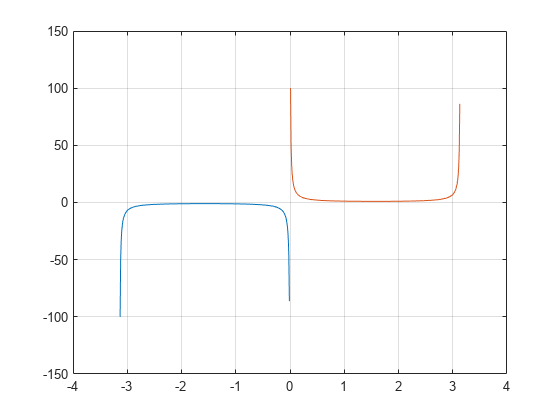

Figure contains an axes object. The axes object contains 2 objects of type line.

ライブ スクリプトを開く

ベクトル x の複素数角度の余割を計算します。

x = [-i pi+i*pi/2 -1+i*4];
y = csc(x)
y = 1×3 complex

   0.0000 + 0.8509i   0.0000 + 0.4345i  -0.0308 - 0.0198i

入力引数

すべて折りたたむ

ラジアン単位の入力角度。スカラー、ベクトル、行列または多次元配列として指定します。

データ型: single | double
複素数のサポート: あり

出力引数

すべて折りたたむ

入力角度の余割。実数値または複素数値のスカラー、ベクトル、行列または多次元配列として返されます。

詳細

すべて折りたたむ

余割関数

直角三角形を基準にして定義される角度 α の余割は、次のようになります。

csc(α)=1sin(α)=hypotenuseopposite side=ha .

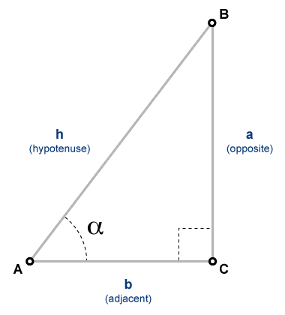
複素数引数 α の余割は次のようになります。

csc(α)=2ieiα−e−iα .

ヒント

  • 浮動小数点演算では、csc は有界の関数です。つまり、csc は、pi の倍数である発散点において Inf や -Inf の値を返さず、代わりに絶対値の大きい数を返します。これは、π の浮動小数点表現が不正確であることに起因します。

拡張機能

C/C++ コード生成
MATLAB® Coder™ を使用して C および C++ コードを生成します。

GPU コード生成
GPU Coder™ を使用して NVIDIA® GPU のための CUDA® コードを生成します。

バージョン履歴

R2006a より前に導入

参考

| | | |