Main Content

データの平滑化と外れ値の検出

ライブ スクリプトを開く

データの平滑化はデータ内の不要なノイズや動作を排除する手法を指し、外れ値の検出は他のデータと著しく異なるデータ点を特定します。

移動ウィンドウ法

移動ウィンドウ法は、通常、データ内の点の近傍を統計的に表すために、1 回の処理を小さいバッチにして複数回データを処理する方法です。移動平均は一般的なデータ平滑化手法であり、データに沿ってウィンドウをスライドさせ、各ウィンドウ内の点の平均を計算します。これは、あるデータ点から次のデータ点への重要ではない変動を排除するために役立ちます。

たとえば、毎分間隔で 3 時間程度行う風速の測定について考えてみます。関数 movmean を 5 分のウィンドウ サイズで使用して、高速の突風を平滑化します。

load windData.mat
mins = 1:length(speed);
window = 5;
meanspeed = movmean(speed,window);
plot(mins,speed,mins,meanspeed)
axis tight
legend("Measured Wind Speed","Average Wind Speed over 5 min Window")
xlabel("Time")
ylabel("Speed")

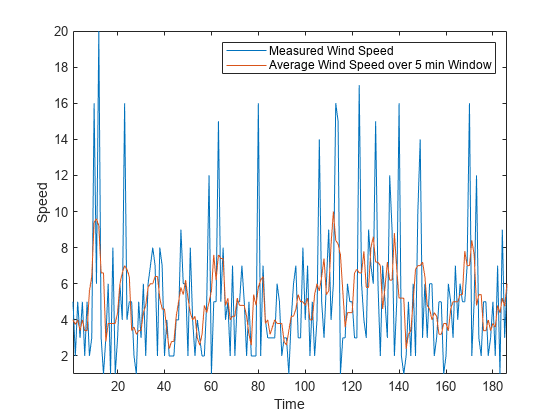
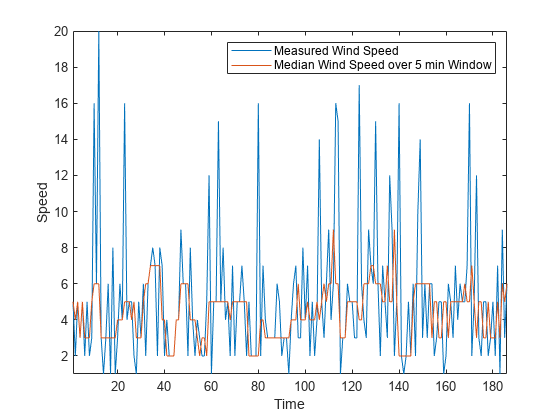
同様に、関数 movmedian を使用すると、スライディング ウィンドウで風速の中央値を計算できます。

medianspeed = movmedian(speed,window);
plot(mins,speed,mins,medianspeed)
axis tight
legend("Measured Wind Speed","Median Wind Speed over 5 min Window")
xlabel("Time")
ylabel("Speed")

すべてのデータが移動ウィンドウ法による平滑化に適しているわけではありません。たとえば、ランダムなノイズを挿入して正弦波信号を作成します。

t = 1:0.2:15;
A = sin(2*pi*t) + cos(2*pi*0.5*t);
Anoise = A + 0.5*rand(1,length(t));
plot(t,A,t,Anoise)
axis tight
legend("Original Data","Noisy Data")

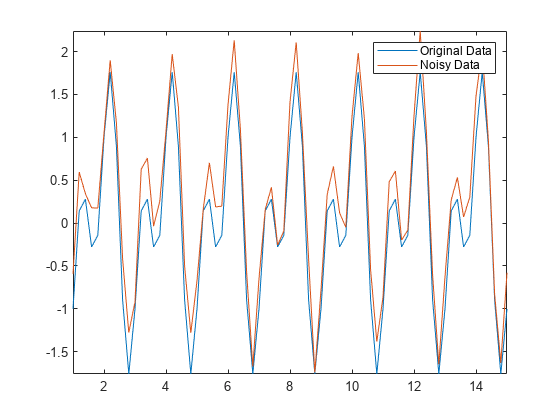
3 のウィンドウ サイズで移動平均を使用して、ノイズを含むデータを平滑化します。

window = 3;
Amean = movmean(Anoise,window);
plot(t,A,t,Amean)
axis tight
legend("Original Data","Moving Mean - Window Size 3")

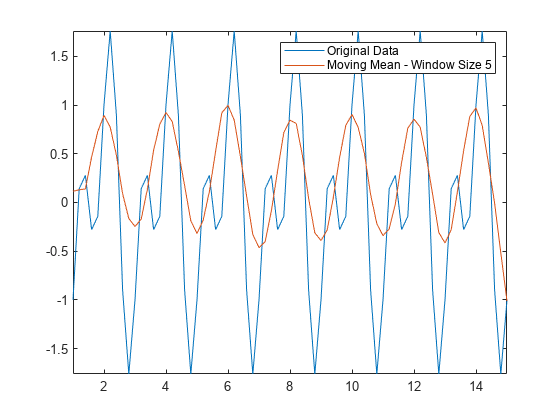
移動平均ではデータの全体的な形状が表示されますが、谷 (局所的最小値) は正確に捕捉されません。谷の点は各ウィンドウの 2 つの大きな近傍に囲まれているため、平均はそれらの点の適切な近似とはなりません。ウィンドウ サイズを大きくすると、平均では短いピークも排除されます。このタイプのデータの場合は、代替の平滑化手法を検討してください。 

Amean = movmean(Anoise,5);
plot(t,A,t,Amean)
axis tight
legend("Original Data","Moving Mean - Window Size 5")

一般的な平滑化法

関数 smoothdata は、信号処理で使用される一般的な平滑化手法である Savitzky-Golay 法など、いくつかの平滑化オプションを提供しています。既定では、smoothdata はデータに応じて、手法に対し最適と推定されるウィンドウ サイズを選択します。

Savitzky–Golay 法を使用してノイズを含む信号 Anoise を平滑化し、使用するウィンドウ サイズを出力します。この手法では、movmean と比較して、より適切な谷の近似が提供されます。 

[Asgolay,window] = smoothdata(Anoise,"sgolay");
plot(t,A,t,Asgolay)
axis tight
legend("Original Data","Savitzky-Golay","location","best")

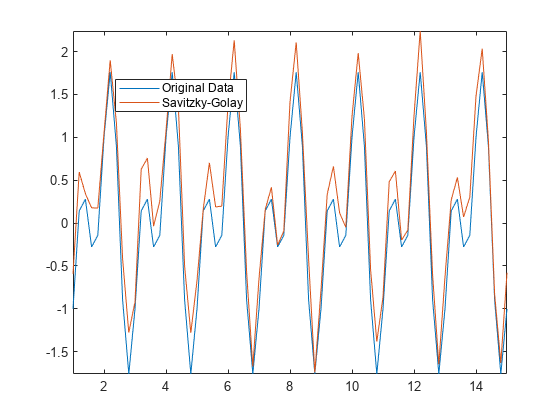
window
window = 3

ロバストな Lowess 法は、ノイズに加えて外れ値がデータに存在する場合に特に役立つ別の平滑化手法です。ノイズを含むデータに外れ値を挿入し、ロバストな Lowess を使用してデータを平滑化します。これにより、外れ値が排除されます。 

Anoise(36) = 20;
Arlowess = smoothdata(Anoise,"rlowess",5);
plot(t,Anoise,t,Arlowess)
axis tight
legend("Noisy Data","Robust Lowess")

外れ値の検出

データ内の外れ値によって、データ処理の結果や他の計算される量が著しく歪められることがあります。たとえば、移動中央値を使用して外れ値を含むデータを平滑化しようとすると、誤ったピークや谷が出現することがあります。 

Amedian = smoothdata(Anoise,"movmedian");
plot(t,Anoise,t,Amedian)
axis tight
legend("Noisy Data","Moving Median")

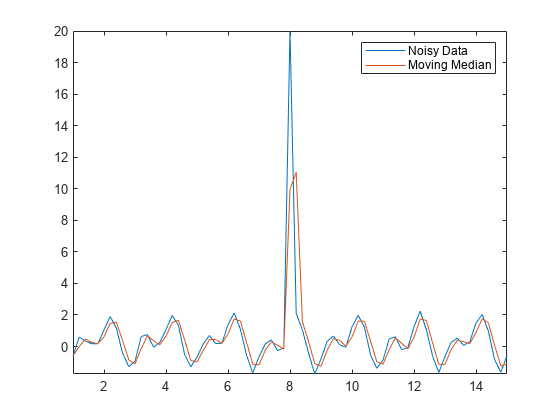
外れ値が検出された場合、関数 isoutlier は logical 1 を返します。Anoise で外れ値のインデックスと値を確認します。

TF = isoutlier(Anoise);
ind = find(TF)
ind = 36

Aoutlier = Anoise(ind)
Aoutlier = 20

関数 filloutliers を使用し、埋め込みメソッドを指定することによって、データ内の外れ値を置き換えることができます。たとえば、Anoise の外れ値にすぐ右の近傍値を埋め込みます。

Afill = filloutliers(Anoise,"next");
plot(t,Anoise,t,Afill,"o-")
axis tight
legend("Noisy Data with Outlier","Noisy Data with Filled Outlier")

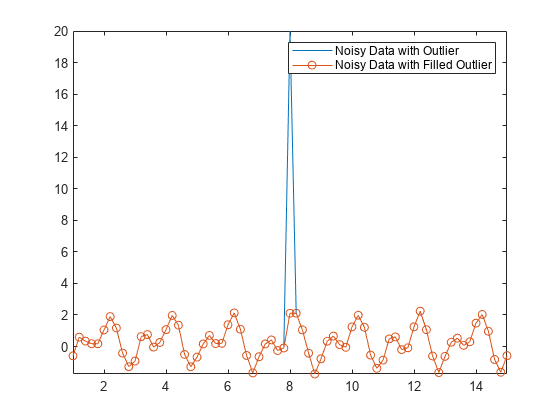
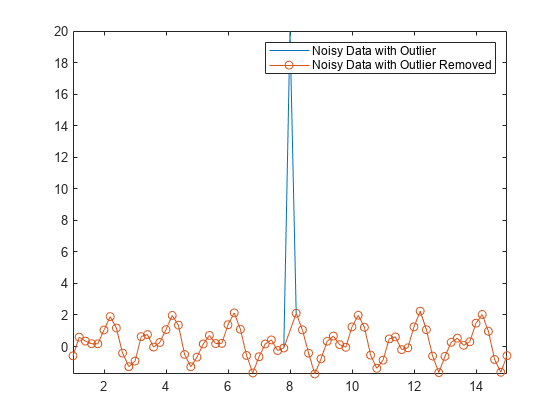
あるいは、関数 rmoutliers を使用することによって、データから外れ値を削除できます。たとえば、Anoise の外れ値を削除します。

Aremove = rmoutliers(Anoise);
plot(t,Anoise,t(~TF),Aremove,"o-")
axis tight
legend("Noisy Data with Outlier","Noisy Data with Outlier Removed")

非等間隔データ

すべてのデータが等間隔に配置された点で構成されているわけではなく、それがデータ処理の手法に影響することがあります。Airreg 内のデータに対し不規則なサンプリング時間が含まれる、datetime ベクトルを作成します。time ベクトルは、最初の 30 分間は毎分、その後の 2 日間は 1 時間ごとに取得されたサンプルを表します。 

t0 = datetime(2014,1,1,1,1,1);
timeminutes = sort(t0 + minutes(1:30));
timehours = t0 + hours(1:48);
time = [timeminutes timehours];
Airreg = rand(1,length(time));
plot(time,Airreg)
axis tight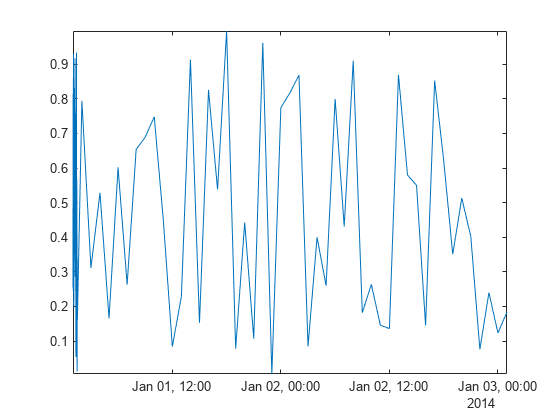

既定では、smoothdata は等間隔の整数 (この場合は 1,2,...,78) について平滑化を行います。整数のタイム スタンプは Airreg の点のサンプリングと対応していないため、最初の 30 分間のデータには平滑化後もノイズが含まれているように見えます。 

Adefault = smoothdata(Airreg,"movmean",3);
plot(time,Airreg,time,Adefault)
axis tight
legend("Original Data","Smoothed Data with Default Sample Points")

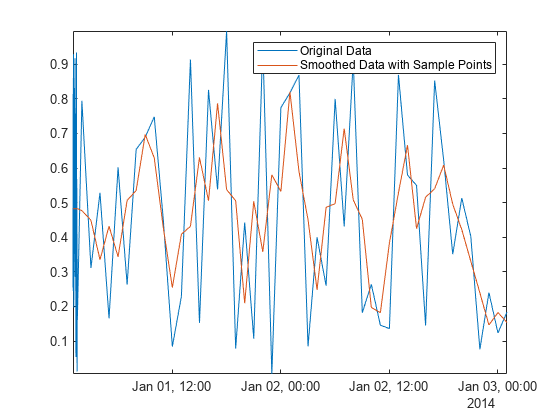
smoothdata、movmean、および filloutliers を含む MATLAB® の多くのデータ処理関数ではサンプル点を指定でき、サンプリングの単位と頻度を基準にしたデータの処理が確保されます。Airreg の最初の 30 分間のデータにある高周波数の変動を削除するには、time のタイム スタンプに名前と値の引数 SamplePoints を使用します。

Asamplepoints = smoothdata(Airreg,"movmean", ...
    hours(3),"SamplePoints",time);
plot(time,Airreg,time,Asamplepoints)
axis tight
legend("Original Data","Smoothed Data with Sample Points")

参考

関数

ライブ エディター タスク

アプリ

関連するトピック