非線形モデル同定の基礎
非線形モデルの同定、ブラックボックスのモデル化、正則化
非線形モデルの同定は、線形モデルではシステムのダイナミクスが完全には捉えられない場合に使用します。非線形モデルは System Identification アプリまたはコマンド ラインで同定できます。System Identification Toolbox™ により、4 種類の非線形モデル構造の作成と推定が可能になります。
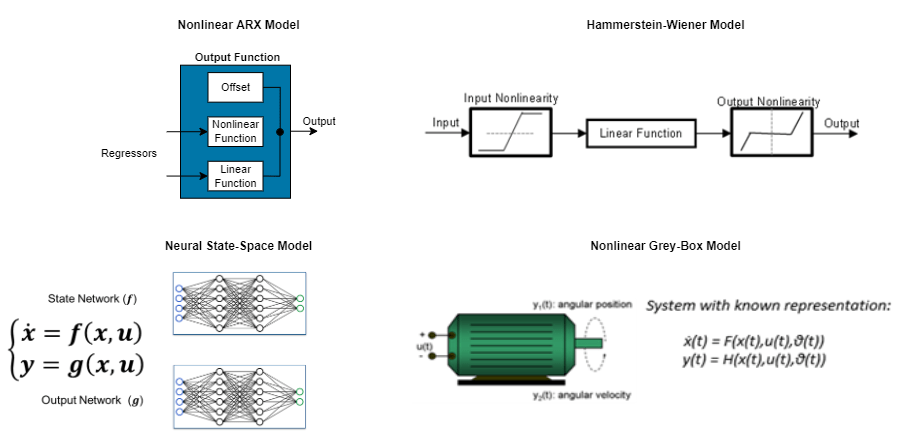
非線形 ARX モデル — ウェーブレット ネットワーク、ツリー分割、シグモイド ネットワークなどの動的な非線形マッピング オブジェクトを使用して、システム内の非線形性を表します。
Hammerstein-Wiener モデル — 線形であるシステムに含まれることがある、静的な非線形性を推定します。
非線形グレー ボックス モデル — 不明のパラメーターを含む常微分方程式または差分方程式 (ODE) を使用して、非線形システムを表します。
ニューラル状態空間モデル — ニューラル ネットワークを使用して、システムの非線形状態空間実現を定義する関数を表します。
トピック
非線形の同定されたモデル
- About Identified Nonlinear Models
Dynamic models in System Identification Toolbox software are mathematical relationships between the inputs u(t) and outputs y(t) of a system. The model is dynamic because the output value at the current time depends on the input-output values at previous time instants. Therefore, dynamic models have memory of the past. You can use the input-output relationships to compute the current output from previous inputs and outputs. Dynamic models have states, where a state vector contains the information of the past. - Nonlinear Model Structures
Construct model objects for nonlinear model structures, access model properties. - Available Nonlinear Models
The System Identification Toolbox software provides four types of nonlinear model structures: - ブラックボックス モデリング
ブラックボックス モデリングは、モデルの特定の数学的構造に関係なくデータを当てはめることに主な関心がある場合に有益です。 - モデル オブジェクトのタイプ
モデル オブジェクト タイプには、固定係数をもつシステムを表すための数値モデル、および調整可能な係数または不確かな係数をもつシステムのための一般化モデルがあります。
モデルの推定
- Identify Nonlinear Black-Box Models Using System Identification App
Identify nonlinear black-box models from single-input/single-output (SISO) data using the System Identification app. - Modeling Multiple-Output Systems
Use a multiple-output modeling technique that suits the complexity and internal input-output coupling of your system. - Preparing Data for Nonlinear Identification
Estimating nonlinear ARX and Hammerstein-Wiener models requires uniformly sampled time-domain data. Your data can have one or more input and output channels. - Loss Function and Model Quality Metrics
Configure the loss function that is minimized during parameter estimation. After estimation, use model quality metrics to assess the quality of identified models. - Regularized Estimates of Model Parameters
Regularization is the technique for specifying constraints on the flexibility of a model, thereby reducing uncertainty in the estimated parameter values. - Estimation Report
The estimation report contains information about the results and options used for a model estimation. This report is stored in theReportproperty of the estimated model. The exact contents of the report depend on the estimator function you use to obtain the model. - Next Steps After Getting an Accurate Model
How you can work with identified models.