ストリーミング逆行列 System object の HDL コード生成
この例では、HDL Coder™ でサイズの構成が可能なストリーミング モードの逆行列演算を実装する方法を示します。
行列の逆行列とは
行列 X は、XY = YX = I となる同じサイズの行列 Y が存在する場合に可逆となります (I は単位行列)。この行列 Y を X の逆行列と呼びます。逆行列のない行列は特異行列です。正方行列は、行列式が正確にゼロの場合のみ特異行列となります。
逆行列の計算手順は次のとおりです。
余因子行列の計算
余因子行列の転置
入力行列の行列式の逆数と転置した余因子行列の乗算
例:
A = [4 12 -16;12 37 -43;-16 -43 98];
Cofactors of 'A' will be calculated from matrix of minors
cof(A) = [1777 488 76;488 136 20;76 20 4];Transpose of cofactor matrix will be
(cof(A))' = [1777 488 76;488 136 20;76 20 4];Multiply reciprocal of determinant of 'A' with transpose of cofactor matrix
Ainv = (1/det(A)) * (cof(A))'
= [49.3611 -13.5556 2.1111;-13.5556 3.7778 -0.5556;2.1111 -0.5556 0.1111];逆行列: ガウス ジョルダン消去法
ガウス ジョルダン消去法を使用して行列 A の逆行列を求めるには、A を単位行列 (I) に変形する基本行演算を求め、同じ演算を単位行列 (I) に対して実行して Ainv を取得しなければなりません。
ガウス ジョルダン消去法を使用した逆行列の計算: 最初に行列 A を記述し、その横に [A | I] として単位行列を記述します。
目的は、行変換を適用して A を単位行列にし、右側の行列 I も行変換に加えて最終的に Ainv を得ることです。
Ainv の計算手順は次のとおりです。
行を入れ替える
対角要素を 1 にする
非対角要素を 0 にする
例:
(A) (I)
1 2 3 | 1 0 0
[A | I] = 2 5 3 | 0 1 0
1 0 8 | 0 0 1Find the element with maximum value in the first column and swap the current
row with maximum element row
swap R1 and R2 rows as R2 contains the largest values. 2 5 3 | 0 1 0
= 1 2 3 | 1 0 0
1 0 8 | 0 0 1Make the diagonal element in the first column as '1'
R1 --> R1/2 1 2.5 1.5 | 0 0.5 0
= 1 2 3 | 1 0 0
1 0 8 | 0 0 1
Make the non-diagonal elements in the first column as '0'
R2 --> R2 - R1
R3 --> R3 - R1 1 2.5 1.5 | 0 0.5 0
= 0 -0.5 1.5 | 1 -0.5 0
0 -2.5 6.5 | 0 -0.5 1Now column 1 has diagonal elements '1' and other elements as '0'. This procedure is repeated for remaining columns and matrix A will be reduced to identity matrix, Identity matrix will be reduced to Ainv.
1 0 0 | -40 16 9
= 0 1 0 | 13 -5 -3
0 0 1 | 5 -2 -1
(I) (Ainv)逆行列: コレスキー分解
コレスキー分解を使用した逆行列では、対称正定値行列のみがサポートされます。正定値とは、行列のすべての固有値が正となることを意味します。
次の対称正定値行列 A について考えます。
A = L * L', L is the lower triangular matrix
L' is the transpose of L inv(A) = inv(L * L')
= inv(L') * inv(L)
= (inv(L))' * inv(L) Ainv = Linv' * Linv, Linv is the inverse of lower triangular matrix
Ainv is the inverse of input matrixAinv の計算手順は次のとおりです。
下三角行列の計算 (L)
下三角行列の逆行列の計算 (Linv)
Linv と転置した Linv の乗算
例:
A = [4 12 -16;12 37 -43;-16 -43 98];
Lower triangular matrix(L) will be computed using cholesky decomposition
L = [2 0 0;6 1 0;-8 5 3];Linv will be computed using forward substitution method
Linv = [0.5 0 0;-3 1 0;6.3333 -1.6667 0.3333];Multiply transpose of Linv with Linv
Ainv = Linv' * Linv
= [49.3611 -13.5556 2.1111;-13.5556 3.7778 -0.5556;2.1111 -0.5556 0.1111];ガウス ジョルダン消去法を使用する利点
ガウス ジョルダン消去法はすべての正方行列をサポートします。
ガウス ジョルダン消去法は
singleとdoubleの両方のデータ型をサポートします。
コレスキーの実装の制限
逆行列を計算する行列は対称正定値でなければなりません。
行列の入力データ型は
singleでなければならず、ブロックをNative Floating Pointモードで使用しなければなりません。入力行列のサイズは 64 行 64 列まででなければなりません。
Matrix Inverse のサブシステムのインターフェイス:

Matrix Inverse の端子の説明:

Matrix Inverse の実装
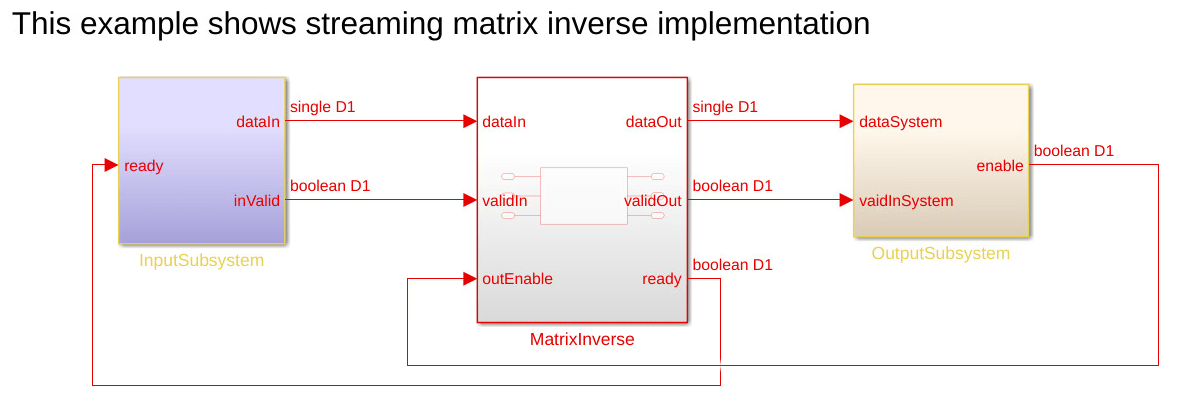
このモデル例には、InputSubsystem、MatrixInverse、および OutputSubsystem の 3 つのサブシステムがあります。上流の InputSubsystem は、ready 信号がイネーブルの場合に行列入力を処理モジュールに直列化するモジュールです。下流の OutputSubsystem は、outEnable 信号がイネーブルの場合に処理モジュールから行列出力にデータを逆シリアル化するモジュールです。MatrixInverse は、逆行列演算を実装する処理モジュールです。
open_system('hdlcoder_streaming_mat_inv_max_lat_cholesky'); open_system('hdlcoder_streaming_mat_inv_max_lat_gauss_jordan');


逆行列のタイミング図:
完全なシステムのタイミング図:
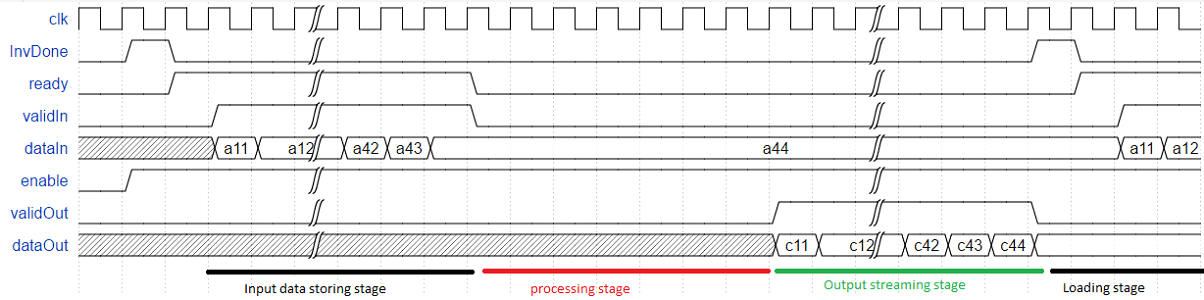
処理段階のタイミング図 (コレスキー分解):

処理段階のタイミング図 (ガウス ジョルダン消去法):

Modelsim の結果の波形 (コレスキー分解)
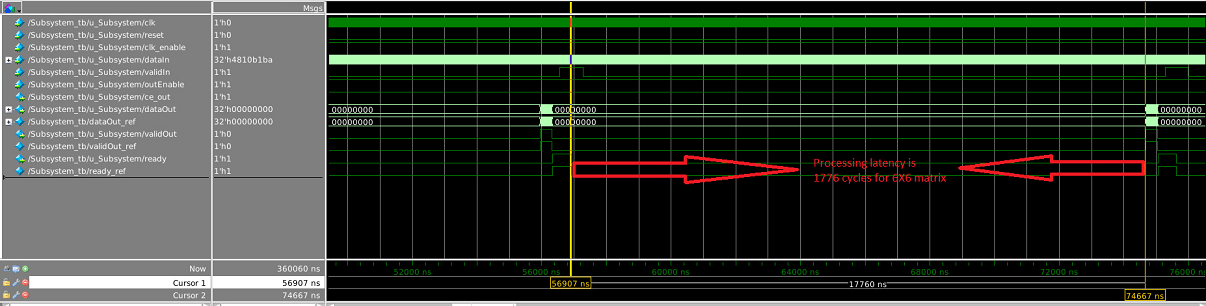
Modelsim の結果の波形 (ガウス ジョルダン消去法)

Matrix Inverse ブロックのパラメーター:
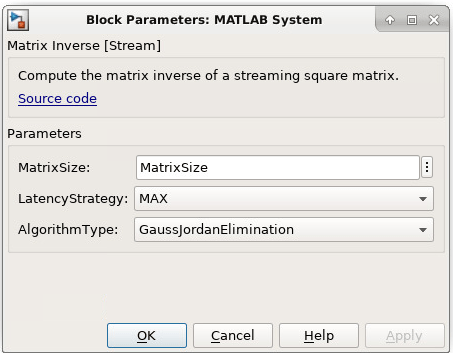
MatrixSize : Enter size of input matrix as a positive integer.
LatencyStrategy : Select latency strategy from drop down menu
({'ZERO, 'MIN', 'MAX'}) which should be same as HDL coder
latency strategy. User can see processing latency
based on the latency strategy.
AlgorithmType : Select algorithm type from drop down menu({'CholeskyDecomposition',
'GaussJordanElimination'})Matrix Inverse ブロックの使用方法
MATLAB System ブロックのブロック パラメーターを設定します。
行列のサイズに基づいて入力行列を選択します。
MatrixInverse サブシステムの HDL コードを生成します。
生成コードと生成モデル
MatrixInverse サブシステムのコード生成の実行後、次のようなコードが生成されます。

生成されるモデルには MatrixInverse MATLAB System ブロックが含まれます。modelsim シミュレーションで、コード生成の出力が MATLAB System ブロックの出力と比較されます。
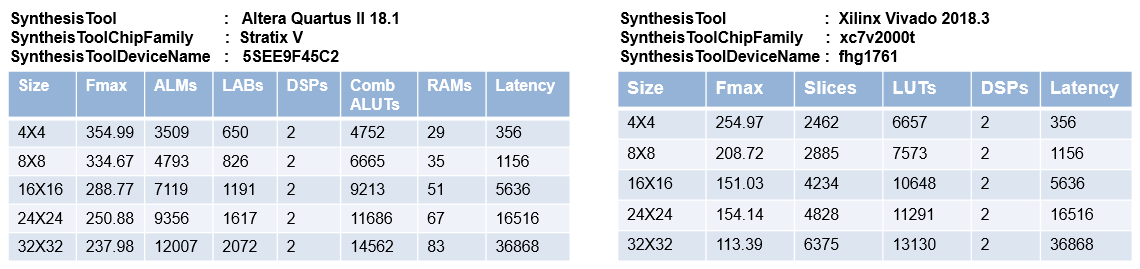
合成の統計
コレスキー分解

ガウス ジョルダン消去法