このページは機械翻訳を使用して翻訳されました。最新版の英語を参照するには、ここをクリックします。
探索とポーリング、問題ベース
メッシュ ポイントをポーリングすることに加えて、パターン探索アルゴリズムは、反復ごとに探索と呼ばれるオプションのステップを実行できます。各反復で、探索ステップは現在のポイントに別の最適化方法を適用します。この探索によって現在のポイントが改善されない場合は、ポーリング手順が実行されます。
この例を実行すると、目的関数 lincontest7 が利用可能になります。
ポーリング方式による探索
次の例は、patternsearch と Optimize ライブエディタータスクを使用した制約付き最小化 で説明されている問題に対する探索方法の使用を示しています。この場合の探索方法は、GSS Positive Basis 2N ポーリングです。比較のために、まずは探索方法を使用せずに問題を実行します。
x = optimvar("x",1,6); prob = optimproblem("Objective",lincontest7(x)); x0.x = [2 1 0 9 1 0]; Aineq = [-8 7 3 -4 9 0]; bineq = 7; Aeq = [7 1 8 3 3 3; 5 0 -5 1 -5 8; -2 -6 7 1 1 9; 1 -1 2 -2 3 -3]; beq = [84 62 65 1]; prob.Constraints.Aineq = Aineq*x' <= bineq; prob.Constraints.Aeq = Aeq*x' == beq'; options = optimoptions('patternsearch',... 'PlotFcn',{@psplotbestf,@psplotfuncount}); [x,fval,exitflag,output] = solve(prob,x0,... "Options",options,"Solver","patternsearch");
Solving problem using patternsearch. patternsearch stopped because the mesh size was less than options.MeshTolerance.
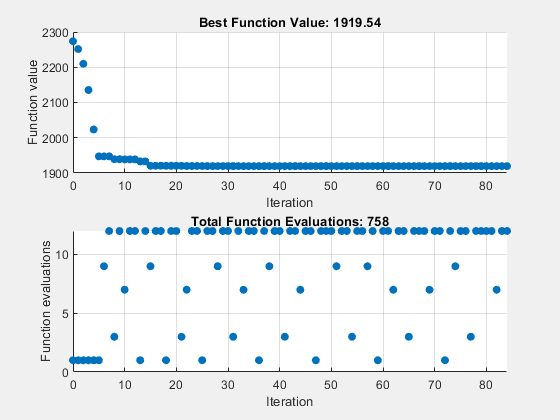
GSS Positive Basis 2N ポーリングを探索方法として使用するには、SearchFcn オプションを変更します。
rng default % For reproducibility options.SearchFcn = @GSSPositiveBasis2N; [x2,fval2,exitflag2,output2] = solve(prob,x0,... "Options",options,"Solver","patternsearch");
Solving problem using patternsearch. patternsearch stopped because the mesh size was less than options.MeshTolerance.
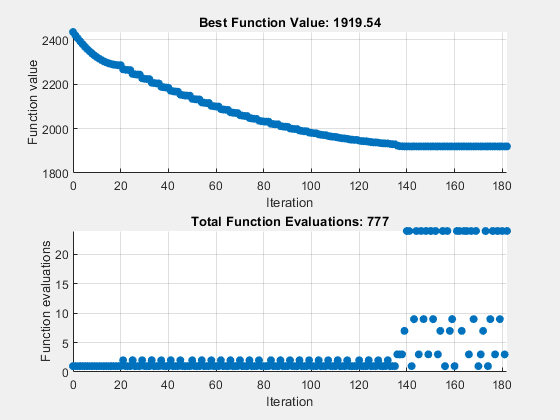
両方の最適化は同じ目的関数の値に到達しました。探索方法を使用すると、関数評価回数は減りますが、反復回数は減りません。
table([output.funccount;output2.funccount],[output.iterations;output2.iterations],... 'VariableNames',["Function Evaluations" "Iterations"],... 'RowNames',["Without Search" "With Search"])
ans=2×2 table
Function Evaluations Iterations
____________________ __________
Without Search 758 84
With Search 667 93
別のソルバーを使用して探索する
patternsearch は、ローゼンブロック関数を最小化するのに長い時間がかかります。関数は次のようになります。
Rosenbrock 関数は [最適化] ライブ エディター タスクまたはソルバーを使用した制約付き非線形問題 で説明され、プロットされています。ローゼンブロック関数の最小値は 0 で、点 [1,1] で達成されます。patternsearch はこの関数を最小化するのに効率的ではないため、別の探索方法を使用してください。
目的関数を作成します。
dejong2fcn = @(x)100*(x(2)-x(1)^2)^2 + (1-x(1))^2;
2 つの変数を使用した patternsearch のデフォルトの最大反復回数は 200 で、関数評価のデフォルトの最大回数は 4000 です。これらの値を MaxFunctionEvaluations = 5000、MaxIterations = 2000 に増やします。
opts = optimoptions("patternsearch","MaxFunctionEvaluations",5000,"MaxIterations",2000);
[-1.9 2] から patternsearch を実行します。
x = optimvar("x",1,2); prob = optimproblem("Objective",dejong2fcn(x)); x0.x = [-1.9,2]; [sol,feval,eflag,output] = solve(prob,x0,... "Options",opts,"Solver","patternsearch");
Solving problem using patternsearch. patternsearch stopped because it exceeded options.MaxFunctionEvaluations.
disp(feval)
0.8560
disp(output.funccount)
5000
5000 回の関数評価後も最適化が完了せず、結果は最適値 0 にあまり近くありません。
関数評価と反復のデフォルト数を使用して、探索方法として fminsearch を使用するようにオプションを設定します。
opts = optimoptions("patternsearch","SearchFcn",@searchneldermead);
最適化を再実行します。
[sol2,feval2,eflag2,output2] = solve(prob,x0,... "Options",opts,"Solver","patternsearch");
Solving problem using patternsearch. patternsearch stopped because the mesh size was less than options.MeshTolerance.
disp(feval2)
4.0686e-10
disp(output2.funccount)
291
この探索方法を使用すると、解における目的関数の値が大幅に改善され (低くなり)、関数評価の回数も大幅に減ります。fminsearch は、Rosenbrock 関数の最小値に近づくのに効率的です。