メモリ効率を高めるためのプログラムによるルックアップ テーブルの最適化
次の例では、メモリ効率の高いルックアップ テーブルをプログラムにより生成する方法を説明します。ルックアップ テーブル オプティマイザーのコマンド ラインにおける同等の操作を使用して、以下を実行できます。
既存の Lookup Table ブロックを最適化する。
Math Function ブロックからルックアップ テーブルを生成する。
関数または関数ハンドルからルックアップ テーブルを生成する。
Subsystem ブロックからルックアップ テーブルを生成する。
ルックアップ テーブルを使用した関数の近似
この例では、関数 sin を近似するメモリ効率の高いルックアップ テーブルを生成する方法を説明します。FunctionApproximation.Problem オブジェクトを作成して近似の問題を定義します。
P = FunctionApproximation.Problem('sin')
P =
1×1 FunctionApproximation.Problem with properties:
FunctionToApproximate: @(x)sin(x)
NumberOfInputs: 1
InputTypes: "numerictype(0,16,13)"
InputLowerBounds: 0
InputUpperBounds: 6.2832
OutputType: "numerictype(1,16,14)"
Options: [1×1 FunctionApproximation.Options]
Problem オブジェクトの FunctionToApproximate プロパティと NumberOfInputs プロパティはオブジェクトの定義から推測され、作成後は編集できません。他のすべてのプロパティは書き込み可能です。
FunctionApproximation.Options オブジェクトを編集して、最適化プロセスで使用する追加の制約を指定します。たとえば、生成されたルックアップ テーブルのブレークポイントを等間隔に制約します。
P.Options.BreakpointSpecification = 'EvenSpacing'
P =
1×1 FunctionApproximation.Problem with properties:
FunctionToApproximate: @(x)sin(x)
NumberOfInputs: 1
InputTypes: "numerictype(0,16,13)"
InputLowerBounds: 0
InputUpperBounds: 6.2832
OutputType: "numerictype(1,16,14)"
Options: [1×1 FunctionApproximation.Options]
出力の絶対許容差と相対許容差などの追加の制約と語長の制約を指定します。
P.Options.AbsTol = 2^-10; P.Options.RelTol = 2^-6; P.Options.WordLengths = [8,16];
solve メソッドを使用して最適化の問題を解決します。MATLAB® には、最適化プロセスの反復回数が表示されます。solve メソッドは FunctionApproximation.LUTSolution オブジェクトを返します。
S = solve(P)
Searching for fixed-point solutions.
| ID | Memory (bits) | Feasible | Table Size | Breakpoints WLs | TableData WL | BreakpointSpecification | Error(Max,Current) |
| 0 | 48 | 0 | 2 | 8 | 16 | EvenSpacing | 9.765625e-04, 1.007261e+00 |
| 1 | 32 | 0 | 2 | 8 | 8 | EvenSpacing | 9.765625e-04, 1.007261e+00 |
| 2 | 672 | 0 | 41 | 8 | 16 | EvenSpacing | 9.765625e-04, 3.322094e-02 |
| 3 | 560 | 0 | 34 | 8 | 16 | EvenSpacing | 9.765625e-04, 9.553784e-02 |
| 4 | 1104 | 0 | 68 | 8 | 16 | EvenSpacing | 9.765625e-04, 1.970943e-03 |
| 5 | 1648 | 1 | 102 | 8 | 16 | EvenSpacing | 9.765625e-04, 7.988139e-05 |
| 6 | 480 | 0 | 29 | 8 | 16 | EvenSpacing | 9.765625e-04, 1.575496e-01 |
| 7 | 832 | 0 | 51 | 8 | 16 | EvenSpacing | 9.765625e-04, 3.322094e-02 |
| 8 | 320 | 0 | 19 | 8 | 16 | EvenSpacing | 9.765625e-04, 9.553784e-02 |
| 9 | 64 | 0 | 2 | 16 | 16 | EvenSpacing | 9.765625e-04, 9.853516e-01 |
| 10 | 48 | 0 | 2 | 16 | 8 | EvenSpacing | 9.765625e-04, 9.853516e-01 |
| 11 | 640 | 1 | 38 | 16 | 16 | EvenSpacing | 9.765625e-04, 6.281694e-04 |
| 12 | 624 | 0 | 37 | 16 | 16 | EvenSpacing | 9.765625e-04, 3.435787e-03 |
| 13 | 496 | 0 | 29 | 16 | 16 | EvenSpacing | 9.765625e-04, 9.943803e-04 |
| 14 | 480 | 0 | 28 | 16 | 16 | EvenSpacing | 9.765625e-04, 1.238521e-03 |
| 15 | 560 | 0 | 33 | 16 | 16 | EvenSpacing | 9.765625e-04, 1.970943e-03 |
| 16 | 592 | 0 | 35 | 16 | 16 | EvenSpacing | 9.765625e-04, 3.679927e-03 |
| 17 | 608 | 0 | 36 | 16 | 16 | EvenSpacing | 9.765625e-04, 2.703365e-03 |
| 18 | 352 | 1 | 20 | 16 | 16 | EvenSpacing | 9.765625e-04, 5.671342e-04 |
| 19 | 336 | 0 | 19 | 16 | 16 | EvenSpacing | 9.765625e-04, 1.325779e-03 |
| 20 | 208 | 0 | 11 | 16 | 16 | EvenSpacing | 9.765625e-04, 3.430176e-02 |
| 21 | 272 | 0 | 15 | 16 | 16 | EvenSpacing | 9.765625e-04, 1.043701e-02 |
| 22 | 304 | 0 | 17 | 16 | 16 | EvenSpacing | 9.765625e-04, 4.526615e-03 |
| 23 | 320 | 0 | 18 | 16 | 16 | EvenSpacing | 9.765625e-04, 2.378452e-03 |
| 24 | 48 | 0 | 2 | 8 | 16 | EvenPow2Spacing | 9.765625e-04, 1.300802e+00 |
| 25 | 224 | 0 | 13 | 8 | 16 | EvenPow2Spacing | 9.765625e-04, 2.794368e-01 |
| 26 | 64 | 0 | 2 | 16 | 16 | EvenPow2Spacing | 9.765625e-04, 1.300802e+00 |
| 27 | 240 | 0 | 13 | 16 | 16 | EvenPow2Spacing | 9.765625e-04, 2.794368e-01 |
| 28 | 1648 | 1 | 102 | 8 | 16 | EvenPow2Spacing | 9.765625e-04, 7.988139e-05 |
Best Solution
| ID | Memory (bits) | Feasible | Table Size | Breakpoints WLs | TableData WL | BreakpointSpecification | Error(Max,Current) |
| 18 | 352 | 1 | 20 | 16 | 16 | EvenSpacing | 9.765625e-04, 5.671342e-04 |
S =
1×1 FunctionApproximation.LUTSolution with properties:
ID: 18
Feasible: "true"
元の関数の数値的動作と解 S に保存されている生成されたルックアップ テーブルの数値的動作を比較します。
err = compare(S)
err =
struct with fields:
Breakpoints: [51473×1 double]
Original: [51473×1 double]
Approximate: [51473×1 double]

LUTSolution オブジェクトに保存されたルックアップ テーブル データにアクセスできます。
t = S.TableData
t =
struct with fields:
BreakpointValues: {[0 0.3307 0.6614 0.9921 1.3228 … ] (1×20 double)}
BreakpointDataTypes: [1×1 embedded.numerictype]
TableValues: [4.2725e-04 0.3278 0.6200 0.8420 … ] (1×20 double)
TableDataType: [1×1 embedded.numerictype]
IsEvenSpacing: 1
Interpolation: Linear
生成された Lookup Table ブロックにアクセスするには、approximate メソッドを使用します。
approximate(S)

既存のルックアップ テーブルの最適化
この例では、メモリの効率を高めるために既存の Lookup Table ブロックを最適化する方法を説明します。最適化する Lookup Table ブロックを含むモデルを開きます。
load_system('sldemo_fuelsys'); open_system('sldemo_fuelsys'); save_system('sldemo_fuelsys','my_sldemo_fuelsys'); open_system('my_sldemo_fuelsys/fuel_rate_control/airflow_calc');

最適化の問題と制約を定義する FunctionApproximation.Problem オブジェクトを作成します。
P = FunctionApproximation.Problem('my_sldemo_fuelsys/fuel_rate_control/airflow_calc/Pumping Constant')
P =
1×1 FunctionApproximation.Problem with properties:
FunctionToApproximate: 'my_sldemo_fuelsys/fuel_rate_control/airflow_calc/Pumping Constant'
NumberOfInputs: 2
InputTypes: ["numerictype('single')" "numerictype('single')"]
InputLowerBounds: [50 0.0500]
InputUpperBounds: [1000 0.9500]
OutputType: "numerictype('single')"
Options: [1×1 FunctionApproximation.Options]
Problem オブジェクト P に関連付けられた Options オブジェクトを変更して追加の制約を指定します。
P.Options.BreakpointSpecification = "EvenSpacing"
P =
1×1 FunctionApproximation.Problem with properties:
FunctionToApproximate: 'my_sldemo_fuelsys/fuel_rate_control/airflow_calc/Pumping Constant'
NumberOfInputs: 2
InputTypes: ["numerictype('single')" "numerictype('single')"]
InputLowerBounds: [50 0.0500]
InputUpperBounds: [1000 0.9500]
OutputType: "numerictype('single')"
Options: [1×1 FunctionApproximation.Options]
最適化の問題を解決します。
S = solve(P)
Performing lossless compression.
| ID | Memory (bits) | Feasible | Table Size | Breakpoints WLs | TableData WL | BreakpointSpecification | Error(Max,Current) |
| 0 | 12128 | 1 | [18 19] | [32 32] | 32 | ExplicitValues | 7.812500e-03, 0.000000e+00 |
| 1 | 11840 | 1 | [18 19] | [16 32] | 32 | ExplicitValues | 7.812500e-03, 0.000000e+00 |
Searching for fixed-point solutions.
| 2 | 80 | 0 | [2 2] | [16 8] | 8 | EvenSpacing | 7.812500e-03, 1.047644e-01 |
| 3 | 336 | 0 | [6 6] | [16 8] | 8 | EvenSpacing | 7.812500e-03, 5.359918e-02 |
| 4 | 288 | 0 | [5 6] | [16 8] | 8 | EvenSpacing | 7.812500e-03, 5.763347e-02 |
| 5 | 288 | 0 | [6 5] | [16 8] | 8 | EvenSpacing | 7.812500e-03, 5.852515e-02 |
| 6 | 248 | 0 | [5 5] | [16 8] | 8 | EvenSpacing | 7.812500e-03, 6.254357e-02 |
| 7 | 1016 | 0 | [11 11] | [16 8] | 8 | EvenSpacing | 7.812500e-03, 3.732740e-02 |
| 8 | 928 | 0 | [10 11] | [16 8] | 8 | EvenSpacing | 7.812500e-03, 3.980108e-02 |
| 9 | 928 | 0 | [11 10] | [16 8] | 8 | EvenSpacing | 7.812500e-03, 3.733837e-02 |
| 10 | 848 | 0 | [10 10] | [16 8] | 8 | EvenSpacing | 7.812500e-03, 3.981027e-02 |
| 11 | 3408 | 0 | [21 20] | [16 8] | 8 | EvenSpacing | 7.812500e-03, 3.073816e-02 |
| 12 | 3248 | 0 | [20 20] | [16 8] | 8 | EvenSpacing | 7.812500e-03, 3.182055e-02 |
| 13 | 7008 | 0 | [29 30] | [16 8] | 8 | EvenSpacing | 7.812500e-03, 3.203207e-02 |
| 14 | 9024 | 0 | [33 34] | [16 8] | 8 | EvenSpacing | 7.812500e-03, 2.947415e-02 |
| 15 | 9568 | 0 | [35 34] | [16 8] | 8 | EvenSpacing | 7.812500e-03, 2.693991e-02 |
| 16 | 9840 | 0 | [36 34] | [16 8] | 8 | EvenSpacing | 7.812500e-03, 2.693303e-02 |
| 17 | 11592 | 0 | [37 39] | [16 8] | 8 | EvenSpacing | 7.812500e-03, 2.697569e-02 |
| 18 | 840 | 0 | [9 11] | [16 8] | 8 | EvenSpacing | 7.812500e-03, 4.113068e-02 |
| 19 | 768 | 0 | [9 10] | [16 8] | 8 | EvenSpacing | 7.812500e-03, 4.113972e-02 |
| 20 | 3088 | 0 | [19 20] | [16 8] | 8 | EvenSpacing | 7.812500e-03, 3.294589e-02 |
| 21 | 2928 | 0 | [18 20] | [16 8] | 8 | EvenSpacing | 7.812500e-03, 3.402773e-02 |
| 22 | 11280 | 0 | [36 39] | [16 8] | 8 | EvenSpacing | 7.812500e-03, 2.696199e-02 |
| 23 | 1848 | 0 | [15 15] | [16 8] | 8 | EvenSpacing | 7.812500e-03, 3.395228e-02 |
| 24 | 1728 | 0 | [14 15] | [16 8] | 8 | EvenSpacing | 7.812500e-03, 3.526947e-02 |
| 25 | 1728 | 0 | [15 14] | [16 8] | 8 | EvenSpacing | 7.812500e-03, 3.394671e-02 |
| 26 | 1616 | 0 | [14 14] | [16 8] | 8 | EvenSpacing | 7.812500e-03, 3.526382e-02 |
| 27 | 6768 | 0 | [28 30] | [16 8] | 8 | EvenSpacing | 7.812500e-03, 3.200894e-02 |
| 28 | 6080 | 0 | [29 26] | [16 8] | 8 | EvenSpacing | 7.812500e-03, 3.203845e-02 |
| 29 | 5872 | 0 | [28 26] | [16 8] | 8 | EvenSpacing | 7.812500e-03, 3.201495e-02 |
| 30 | 2784 | 0 | [19 18] | [16 8] | 8 | EvenSpacing | 7.812500e-03, 3.294266e-02 |
| 31 | 2640 | 0 | [18 18] | [16 8] | 8 | EvenSpacing | 7.812500e-03, 3.402446e-02 |
| 32 | 128 | 0 | [2 2] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 1.050016e-01 |
| 33 | 384 | 0 | [6 6] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 5.586732e-02 |
| 34 | 336 | 0 | [5 6] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 5.984281e-02 |
| 35 | 336 | 0 | [6 5] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 6.017429e-02 |
| 36 | 296 | 0 | [5 5] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 6.432428e-02 |
| 37 | 1064 | 0 | [11 11] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 3.045144e-02 |
| 38 | 976 | 0 | [10 11] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 3.175086e-02 |
| 39 | 976 | 0 | [11 10] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 3.294543e-02 |
| 40 | 896 | 0 | [10 10] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 3.428509e-02 |
| 41 | 3624 | 0 | [21 21] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 1.122022e-02 |
| 42 | 3456 | 0 | [20 21] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 1.230498e-02 |
| 43 | 3456 | 0 | [21 20] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 1.122023e-02 |
| 44 | 3296 | 0 | [20 20] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 1.230499e-02 |
| 45 | 6824 | 1 | [29 29] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 5.942483e-03 |
| 46 | 5096 | 0 | [25 25] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 1.073996e-02 |
| 47 | 5928 | 0 | [27 27] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 9.911638e-03 |
| 48 | 6368 | 0 | [28 28] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 9.591103e-03 |
| 49 | 888 | 0 | [9 11] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 3.301938e-02 |
| 50 | 816 | 0 | [9 10] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 3.557669e-02 |
| 51 | 3288 | 0 | [19 21] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 1.348407e-02 |
| 52 | 3120 | 0 | [18 21] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 1.477948e-02 |
| 53 | 3136 | 0 | [19 20] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 1.348408e-02 |
| 54 | 2976 | 0 | [18 20] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 1.477949e-02 |
| 55 | 4704 | 0 | [24 24] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 1.143900e-02 |
| 56 | 5504 | 0 | [26 26] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 1.015224e-02 |
| 57 | 1896 | 0 | [15 15] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 1.782543e-02 |
| 58 | 1776 | 0 | [14 15] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 1.896208e-02 |
| 59 | 1776 | 0 | [15 14] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 2.033137e-02 |
| 60 | 1664 | 0 | [14 14] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 2.102681e-02 |
| 61 | 6592 | 0 | [28 29] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 9.233050e-03 |
| 62 | 6592 | 0 | [29 28] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 9.317551e-03 |
| 63 | 2984 | 0 | [19 19] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 1.348408e-02 |
| 64 | 2832 | 0 | [18 19] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 1.477949e-02 |
| 65 | 3576 | 0 | [15 29] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 1.782529e-02 |
| 66 | 5200 | 0 | [22 29] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 1.141367e-02 |
| 67 | 5896 | 0 | [25 29] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 1.040211e-02 |
| 68 | 6360 | 0 | [27 29] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 9.623498e-03 |
| 69 | 3576 | 0 | [29 15] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 1.082240e-02 |
| 70 | 5200 | 1 | [29 22] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 4.581798e-03 |
| 71 | 4272 | 1 | [29 18] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 6.252181e-03 |
| 72 | 3808 | 0 | [29 16] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 9.142157e-03 |
| 73 | 4040 | 1 | [29 17] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 4.846454e-03 |
| 74 | 112 | 0 | [2 2] | [16 8] | 16 | EvenSpacing | 7.812500e-03, 1.054419e-01 |
| 75 | 624 | 0 | [6 6] | [16 8] | 16 | EvenSpacing | 7.812500e-03, 5.441361e-02 |
| 76 | 528 | 0 | [5 6] | [16 8] | 16 | EvenSpacing | 7.812500e-03, 5.850272e-02 |
| 77 | 528 | 0 | [6 5] | [16 8] | 16 | EvenSpacing | 7.812500e-03, 5.939556e-02 |
| 78 | 448 | 0 | [5 5] | [16 8] | 16 | EvenSpacing | 7.812500e-03, 6.330952e-02 |
| 79 | 1984 | 0 | [11 11] | [16 8] | 16 | EvenSpacing | 7.812500e-03, 3.819569e-02 |
| 80 | 1808 | 0 | [10 11] | [16 8] | 16 | EvenSpacing | 7.812500e-03, 4.053834e-02 |
| 81 | 1808 | 0 | [11 10] | [16 8] | 16 | EvenSpacing | 7.812500e-03, 3.820685e-02 |
| 82 | 1648 | 0 | [10 10] | [16 8] | 16 | EvenSpacing | 7.812500e-03, 4.054764e-02 |
| 83 | 2752 | 0 | [13 13] | [16 8] | 16 | EvenSpacing | 7.812500e-03, 3.728967e-02 |
| 84 | 3184 | 0 | [14 14] | [16 8] | 16 | EvenSpacing | 7.812500e-03, 3.594763e-02 |
| 85 | 3648 | 0 | [15 15] | [16 8] | 16 | EvenSpacing | 7.812500e-03, 3.461587e-02 |
| 86 | 1632 | 0 | [9 11] | [16 8] | 16 | EvenSpacing | 7.812500e-03, 4.186375e-02 |
| 87 | 1488 | 0 | [9 10] | [16 8] | 16 | EvenSpacing | 7.812500e-03, 4.187307e-02 |
| 88 | 3408 | 0 | [14 15] | [16 8] | 16 | EvenSpacing | 7.812500e-03, 3.595323e-02 |
| 89 | 3408 | 0 | [15 14] | [16 8] | 16 | EvenSpacing | 7.812500e-03, 3.461035e-02 |
| 90 | 160 | 0 | [2 2] | [16 32] | 16 | EvenSpacing | 7.812500e-03, 1.056961e-01 |
| 91 | 672 | 0 | [6 6] | [16 32] | 16 | EvenSpacing | 7.812500e-03, 5.636005e-02 |
| 92 | 576 | 0 | [5 6] | [16 32] | 16 | EvenSpacing | 7.812500e-03, 6.042351e-02 |
| 93 | 576 | 0 | [6 5] | [16 32] | 16 | EvenSpacing | 7.812500e-03, 6.089346e-02 |
| 94 | 496 | 0 | [5 5] | [16 32] | 16 | EvenSpacing | 7.812500e-03, 6.486014e-02 |
| 95 | 2032 | 0 | [11 11] | [16 32] | 16 | EvenSpacing | 7.812500e-03, 3.086447e-02 |
| 96 | 1856 | 0 | [10 11] | [16 32] | 16 | EvenSpacing | 7.812500e-03, 3.200457e-02 |
| 97 | 1856 | 0 | [11 10] | [16 32] | 16 | EvenSpacing | 7.812500e-03, 3.320324e-02 |
| 98 | 1696 | 0 | [10 10] | [16 32] | 16 | EvenSpacing | 7.812500e-03, 3.437613e-02 |
| 99 | 2800 | 0 | [13 13] | [16 32] | 16 | EvenSpacing | 7.812500e-03, 2.426444e-02 |
| 100 | 3232 | 0 | [14 14] | [16 32] | 16 | EvenSpacing | 7.812500e-03, 2.114150e-02 |
| 101 | 3696 | 0 | [15 15] | [16 32] | 16 | EvenSpacing | 7.812500e-03, 1.866127e-02 |
| 102 | 1680 | 0 | [9 11] | [16 32] | 16 | EvenSpacing | 7.812500e-03, 3.325658e-02 |
| 103 | 1536 | 0 | [9 10] | [16 32] | 16 | EvenSpacing | 7.812500e-03, 3.565369e-02 |
| 104 | 3456 | 0 | [14 15] | [16 32] | 16 | EvenSpacing | 7.812500e-03, 1.986876e-02 |
| 105 | 3456 | 0 | [15 14] | [16 32] | 16 | EvenSpacing | 7.812500e-03, 2.041715e-02 |
| 106 | 80 | 0 | [2 2] | [16 8] | 8 | EvenPow2Spacing | 7.812500e-03, 8.762427e-02 |
| 107 | 176 | 0 | [4 4] | [16 8] | 8 | EvenPow2Spacing | 7.812500e-03, 6.649438e-02 |
| 108 | 560 | 0 | [8 8] | [16 8] | 8 | EvenPow2Spacing | 7.812500e-03, 4.443537e-02 |
| 109 | 1848 | 0 | [15 15] | [16 8] | 8 | EvenPow2Spacing | 7.812500e-03, 3.130737e-02 |
| 110 | 128 | 0 | [2 2] | [16 32] | 8 | EvenPow2Spacing | 7.812500e-03, 8.876665e-02 |
| 111 | 224 | 0 | [4 4] | [16 32] | 8 | EvenPow2Spacing | 7.812500e-03, 6.768109e-02 |
| 112 | 608 | 0 | [8 8] | [16 32] | 8 | EvenPow2Spacing | 7.812500e-03, 4.280089e-02 |
| 113 | 1896 | 0 | [15 15] | [16 32] | 8 | EvenPow2Spacing | 7.812500e-03, 1.727375e-02 |
| 114 | 112 | 0 | [2 2] | [16 8] | 16 | EvenPow2Spacing | 7.812500e-03, 8.821005e-02 |
| 115 | 304 | 0 | [4 4] | [16 8] | 16 | EvenPow2Spacing | 7.812500e-03, 6.703682e-02 |
| 116 | 1072 | 0 | [8 8] | [16 8] | 16 | EvenPow2Spacing | 7.812500e-03, 4.518663e-02 |
| 117 | 3648 | 0 | [15 15] | [16 8] | 16 | EvenPow2Spacing | 7.812500e-03, 3.193045e-02 |
| 118 | 160 | 0 | [2 2] | [16 32] | 16 | EvenPow2Spacing | 7.812500e-03, 8.949985e-02 |
| 119 | 352 | 0 | [4 4] | [16 32] | 16 | EvenPow2Spacing | 7.812500e-03, 6.804707e-02 |
| 120 | 1120 | 0 | [8 8] | [16 32] | 16 | EvenPow2Spacing | 7.812500e-03, 4.297789e-02 |
| 121 | 3696 | 0 | [15 15] | [16 32] | 16 | EvenPow2Spacing | 7.812500e-03, 1.764470e-02 |
| 122 | 176 | 0 | [2 2] | [16 8] | 32 | EvenPow2Spacing | 7.812500e-03, 8.821114e-02 |
| 123 | 560 | 0 | [4 4] | [16 8] | 32 | EvenPow2Spacing | 7.812500e-03, 6.703763e-02 |
| 124 | 2096 | 0 | [8 8] | [16 8] | 32 | EvenPow2Spacing | 7.812500e-03, 4.518658e-02 |
| 125 | 224 | 0 | [2 2] | [16 32] | 32 | EvenSpacing | 7.812500e-03, 1.056970e-01 |
| 126 | 1248 | 0 | [6 6] | [16 32] | 32 | EvenSpacing | 7.812500e-03, 5.636011e-02 |
| 127 | 1056 | 0 | [5 6] | [16 32] | 32 | EvenSpacing | 7.812500e-03, 6.042374e-02 |
| 128 | 1056 | 0 | [6 5] | [16 32] | 32 | EvenSpacing | 7.812500e-03, 6.089350e-02 |
| 129 | 896 | 0 | [5 5] | [16 32] | 32 | EvenSpacing | 7.812500e-03, 6.485981e-02 |
| 130 | 3968 | 0 | [11 11] | [16 32] | 32 | EvenSpacing | 7.812500e-03, 3.086332e-02 |
| 131 | 3616 | 0 | [10 11] | [16 32] | 32 | EvenSpacing | 7.812500e-03, 3.200400e-02 |
| 132 | 3616 | 0 | [11 10] | [16 32] | 32 | EvenSpacing | 7.812500e-03, 3.320256e-02 |
| 133 | 3296 | 0 | [10 10] | [16 32] | 32 | EvenSpacing | 7.812500e-03, 3.437598e-02 |
| 134 | 3264 | 0 | [9 11] | [16 32] | 32 | EvenSpacing | 7.812500e-03, 3.325607e-02 |
| 135 | 2976 | 0 | [9 10] | [16 32] | 32 | EvenSpacing | 7.812500e-03, 3.565340e-02 |
| 136 | 224 | 0 | [2 2] | [16 32] | 32 | EvenPow2Spacing | 7.812500e-03, 8.950082e-02 |
| 137 | 608 | 0 | [4 4] | [16 32] | 32 | EvenPow2Spacing | 7.812500e-03, 6.804725e-02 |
| 138 | 2144 | 0 | [8 8] | [16 32] | 32 | EvenPow2Spacing | 7.812500e-03, 4.297808e-02 |
Searching for floating-point solutions.
| 139 | 128 | 0 | [2 2] | [16 16] | 16 | EvenSpacing | 7.812500e-03, 1.056933e-01 |
| 140 | 640 | 0 | [6 6] | [16 16] | 16 | EvenSpacing | 7.812500e-03, 1.070723e-01 |
| 141 | 544 | 0 | [5 6] | [16 16] | 16 | EvenSpacing | 7.812500e-03, 1.167613e-01 |
| 142 | 544 | 0 | [6 5] | [16 16] | 16 | EvenSpacing | 7.812500e-03, 1.070723e-01 |
| 143 | 464 | 0 | [5 5] | [16 16] | 16 | EvenSpacing | 7.812500e-03, 1.167613e-01 |
| 144 | 2000 | 0 | [11 11] | [16 16] | 16 | EvenSpacing | 7.812500e-03, 7.649525e-02 |
| 145 | 1824 | 0 | [10 11] | [16 16] | 16 | EvenSpacing | 7.812500e-03, 8.041156e-02 |
| 146 | 1824 | 0 | [11 10] | [16 16] | 16 | EvenSpacing | 7.812500e-03, 7.557118e-02 |
| 147 | 1664 | 0 | [10 10] | [16 16] | 16 | EvenSpacing | 7.812500e-03, 7.940072e-02 |
| 148 | 2768 | 0 | [13 13] | [16 16] | 16 | EvenSpacing | 7.812500e-03, 6.440965e-02 |
| 149 | 3200 | 0 | [14 14] | [16 16] | 16 | EvenSpacing | 7.812500e-03, 6.104388e-02 |
| 150 | 3664 | 0 | [15 15] | [16 16] | 16 | EvenSpacing | 7.812500e-03, 5.459525e-02 |
| 151 | 1648 | 0 | [9 11] | [16 16] | 16 | EvenSpacing | 7.812500e-03, 8.252526e-02 |
| 152 | 1504 | 0 | [9 10] | [16 16] | 16 | EvenSpacing | 7.812500e-03, 8.145604e-02 |
| 153 | 2368 | 0 | [12 12] | [16 16] | 16 | EvenSpacing | 7.812500e-03, 6.633021e-02 |
| 154 | 3424 | 0 | [14 15] | [16 16] | 16 | EvenSpacing | 7.812500e-03, 6.174578e-02 |
| 155 | 3424 | 0 | [15 14] | [16 16] | 16 | EvenSpacing | 7.812500e-03, 5.392386e-02 |
| 156 | 192 | 0 | [2 2] | [16 16] | 32 | EvenSpacing | 7.812500e-03, 1.056982e-01 |
| 157 | 1216 | 0 | [6 6] | [16 16] | 32 | EvenSpacing | 7.812500e-03, 1.070601e-01 |
| 158 | 1024 | 0 | [5 6] | [16 16] | 32 | EvenSpacing | 7.812500e-03, 1.167491e-01 |
| 159 | 1024 | 0 | [6 5] | [16 16] | 32 | EvenSpacing | 7.812500e-03, 1.070601e-01 |
| 160 | 864 | 0 | [5 5] | [16 16] | 32 | EvenSpacing | 7.812500e-03, 1.167491e-01 |
| 161 | 3936 | 0 | [11 11] | [16 16] | 32 | EvenSpacing | 7.812500e-03, 7.648305e-02 |
| 162 | 3584 | 0 | [10 11] | [16 16] | 32 | EvenSpacing | 7.812500e-03, 8.041827e-02 |
| 163 | 3584 | 0 | [11 10] | [16 16] | 32 | EvenSpacing | 7.812500e-03, 7.556098e-02 |
| 164 | 3264 | 0 | [10 10] | [16 16] | 32 | EvenSpacing | 7.812500e-03, 7.939874e-02 |
| 165 | 3232 | 0 | [9 11] | [16 16] | 32 | EvenSpacing | 7.812500e-03, 8.252769e-02 |
| 166 | 2944 | 0 | [9 10] | [16 16] | 32 | EvenSpacing | 7.812500e-03, 8.144822e-02 |
| 167 | 128 | 0 | [2 2] | [16 16] | 16 | EvenPow2Spacing | 7.812500e-03, 1.802750e-01 |
| 168 | 1088 | 0 | [8 8] | [16 16] | 16 | EvenPow2Spacing | 7.812500e-03, 1.016312e-01 |
| 169 | 576 | 0 | [4 8] | [16 16] | 16 | EvenPow2Spacing | 7.812500e-03, 1.452409e-01 |
| 170 | 576 | 0 | [8 4] | [16 16] | 16 | EvenPow2Spacing | 7.812500e-03, 1.334611e-01 |
| 171 | 320 | 0 | [4 4] | [16 16] | 16 | EvenPow2Spacing | 7.812500e-03, 1.568986e-01 |
| 172 | 3664 | 0 | [15 15] | [16 16] | 16 | EvenPow2Spacing | 7.812500e-03, 1.016312e-01 |
| 173 | 192 | 0 | [2 2] | [16 16] | 32 | EvenPow2Spacing | 7.812500e-03, 1.802654e-01 |
| 174 | 2112 | 0 | [8 8] | [16 16] | 32 | EvenPow2Spacing | 7.812500e-03, 1.016435e-01 |
| 175 | 1088 | 0 | [4 8] | [16 16] | 32 | EvenPow2Spacing | 7.812500e-03, 1.452515e-01 |
| 176 | 1088 | 0 | [8 4] | [16 16] | 32 | EvenPow2Spacing | 7.812500e-03, 1.334589e-01 |
| 177 | 576 | 0 | [4 4] | [16 16] | 32 | EvenPow2Spacing | 7.812500e-03, 1.568881e-01 |
| 178 | 160 | 0 | [2 2] | [16 32] | 16 | EvenPow2Spacing | 7.812500e-03, 1.802750e-01 |
| 179 | 1120 | 0 | [8 8] | [16 32] | 16 | EvenPow2Spacing | 7.812500e-03, 1.015092e-01 |
| 180 | 608 | 0 | [4 8] | [16 32] | 16 | EvenPow2Spacing | 7.812500e-03, 1.451798e-01 |
| 181 | 608 | 0 | [8 4] | [16 32] | 16 | EvenPow2Spacing | 7.812500e-03, 1.334611e-01 |
| 182 | 352 | 0 | [4 4] | [16 32] | 16 | EvenPow2Spacing | 7.812500e-03, 1.568986e-01 |
| 183 | 3696 | 0 | [15 15] | [16 32] | 16 | EvenPow2Spacing | 7.812500e-03, 1.015092e-01 |
| 184 | 224 | 0 | [2 2] | [16 32] | 32 | EvenPow2Spacing | 7.812500e-03, 1.802723e-01 |
| 185 | 2144 | 0 | [8 8] | [16 32] | 32 | EvenPow2Spacing | 7.812500e-03, 1.015072e-01 |
| 186 | 1120 | 0 | [4 8] | [16 32] | 32 | EvenPow2Spacing | 7.812500e-03, 1.451943e-01 |
| 187 | 1120 | 0 | [8 4] | [16 32] | 32 | EvenPow2Spacing | 7.812500e-03, 1.334522e-01 |
| 188 | 608 | 0 | [4 4] | [16 32] | 32 | EvenPow2Spacing | 7.812500e-03, 1.568892e-01 |
Best Solution
| ID | Memory (bits) | Feasible | Table Size | Breakpoints WLs | TableData WL | BreakpointSpecification | Error(Max,Current) |
| 73 | 4040 | 1 | [29 17] | [16 32] | 8 | EvenSpacing | 7.812500e-03, 4.846454e-03 |
S =
1×1 FunctionApproximation.LUTSolution with properties:
ID: 73
Feasible: "true"
元のルックアップ テーブルの数値的動作を、最適化されたルックアップ テーブルと比較します。
compare(S)
ans =
1×2 struct array with fields:
Breakpoints
Original
Approximate

approximate メソッドを使用して新しい Lookup Table ブロックを生成します。
S.approximate

%#ok<*NOPTS>
メモリの最適化と絶対許容誤差の比較を示すパレート フロントの可視化
メモリと絶対許容誤差の両方を最適化する場合は、この 2 つのトレードオフを可視化すると役に立ちます。この例では、絶対許容誤差のさまざまなレベルを使用して関数 1-exp(-x) のルックアップ テーブル近似を作成し、検出された各解のプロットを作成します。最終的なプロットには、メモリの効率と数値忠実度のトレードオフを表示できます。
nTol = 32; % Initialize variables solutions = cell(1,nTol); objectiveValues = cell(1,nTol); constraintValues = cell(1,nTol); memoryUnits = 'bytes'; % Options for absolute tolerance absTol = 2.^linspace(-12,-4,nTol); % Relative tolerance is set to 0 relTol = 0; % Initialize options options = FunctionApproximation.Options( ... 'RelTol', relTol, ... 'BreakpointSpecification', 'EvenSpacing', ... 'Display', false, ... 'WordLengths', 16); % Setup the approximation problem problem = FunctionApproximation.Problem( ... @(x) 1 - exp(-x), ... 'InputTypes',numerictype(0,16), ... 'OutputType',numerictype(1,16,14), ... 'InputLowerBounds',0, ... 'InputUpperBounds',5, ... 'Options',options); % Execute to find solutions with different tolerances for iTol = 1:nTol problem.Options.AbsTol = absTol(iTol); solution = solve(problem); objectiveValues{iTol} = arrayfun(@(x) x.totalMemoryUsage(memoryUnits), solution.AllSolutions); constraintValues{iTol} = arrayfun(@(x) x.Feasible, solution.AllSolutions); solutions{iTol} = solution; end % Plot results h = figure(); hold on; for iTol = 1:nTol for iObjective = 1:numel(objectiveValues{iTol}) if constraintValues{iTol}(iObjective) markerColor = 'g'; else markerColor = 'r'; end plot(absTol(iTol),objectiveValues{iTol}(iObjective), ... 'Marker', '.' ,'LineStyle', 'none', ... 'MarkerSize', 24, ... 'MarkerEdgeColor', markerColor) end end xlabel('AbsTol') ylabel(['MemoryUsage (',memoryUnits,')']) h.Children.XScale = 'log'; h.Children.YMinorGrid = 'on'; grid on box on hold off;

実行不可能な解、つまり必要な絶対許容誤差に一致しない解は赤でマークされています。実行可能な解は緑でマークされています。絶対許容誤差が増えると、近似によって、使用するメモリが少ない解が検出されます。絶対許容誤差が小さくなる、つまり数値忠実度が高くなると、必要なメモリも増えます。
曲線上のテーブルの値と曲線外のテーブルの値を使用した近似の比較
この例では、FunctionApproximation.Options オブジェクトの OnCurveTableValues プロパティが true または false に設定されている場合に、関数 tanh に対して生成されたルックアップ テーブル近似を比較します。OnCurveTableValues プロパティは、最適化されたルックアップ テーブルによる近似のテーブル値が近似される元の関数の量子化値の出力と等しいかどうかを指定します。場合によっては、この値を false に設定することで、生成されたルックアップ テーブルによる近似により、ルックアップ テーブルが使用するメモリを削減しながら同じ許容誤差を維持できます。
曲線上のテーブルの値を使用したルックアップ テーブル近似の作成
FunctionApproximation.Problem オブジェクトを使用して、ルックアップ テーブルを使用して近似を行う関数を定義します。既定では、関連付けられている Options オブジェクトの OnCurveTableValues プロパティは false に設定されています。テーブルの値を、近似される関数の量子化された出力に制約するには、このプロパティを true に設定します。
P1 = FunctionApproximation.Problem('tanh');
P1.Options.OnCurveTableValues = 1P1 =
1×1 FunctionApproximation.Problem with properties:
FunctionToApproximate: @(x)tanh(x)
NumberOfInputs: 1
InputTypes: "numerictype(1,16,12)"
InputLowerBounds: -8
InputUpperBounds: 8
OutputType: "numerictype(1,16,15)"
Options: [1×1 FunctionApproximation.Options]
ルックアップ テーブルによる近似を生成します。
S1 = solve(P1)
Searching for fixed-point solutions. | ID | Memory (bits) | Feasible | Table Size | Breakpoints WLs | TableData WL | BreakpointSpecification | Error(Max,Current) | | 0 | 64 | 0 | 2 | 16 | 16 | EvenSpacing | 7.812500e-03, 7.229091e-01 | | 1 | 1248 | 1 | 76 | 16 | 16 | EvenSpacing | 7.812500e-03, 4.368265e-03 | | 2 | 1232 | 1 | 75 | 16 | 16 | EvenSpacing | 7.812500e-03, 4.439035e-03 | | 3 | 944 | 1 | 57 | 16 | 16 | EvenSpacing | 7.812500e-03, 7.780470e-03 | | 4 | 928 | 0 | 56 | 16 | 16 | EvenSpacing | 7.812500e-03, 7.990307e-03 | | 5 | 656 | 0 | 39 | 16 | 16 | EvenSpacing | 7.812500e-03, 1.678519e-02 | | 6 | 640 | 0 | 38 | 16 | 16 | EvenSpacing | 7.812500e-03, 1.660649e-02 | | 7 | 784 | 0 | 47 | 16 | 16 | EvenSpacing | 7.812500e-03, 1.102459e-02 | | 8 | 864 | 0 | 52 | 16 | 16 | EvenSpacing | 7.812500e-03, 9.403441e-03 | | 9 | 896 | 0 | 54 | 16 | 16 | EvenSpacing | 7.812500e-03, 8.643626e-03 | | 10 | 912 | 0 | 55 | 16 | 16 | EvenSpacing | 7.812500e-03, 8.316993e-03 | | 11 | 496 | 0 | 29 | 16 | 16 | EvenSpacing | 7.812500e-03, 2.894880e-02 | | 12 | 720 | 0 | 43 | 16 | 16 | EvenSpacing | 7.812500e-03, 1.355547e-02 | | 13 | 832 | 0 | 50 | 16 | 16 | EvenSpacing | 7.812500e-03, 1.019267e-02 | | 14 | 880 | 0 | 53 | 16 | 16 | EvenSpacing | 7.812500e-03, 8.881069e-03 | | 15 | 448 | 1 | 14 | 16 | 16 | ExplicitValues | 7.812500e-03, 7.801827e-03 | Best Solution | ID | Memory (bits) | Feasible | Table Size | Breakpoints WLs | TableData WL | BreakpointSpecification | Error(Max,Current) | | 15 | 448 | 1 | 14 | 16 | 16 | ExplicitValues | 7.812500e-03, 7.801827e-03 |
S1 =
1×1 FunctionApproximation.LUTSolution with properties:
ID: 15
Feasible: "true"
任意のテーブル値を使用したルックアップ テーブルによる近似の作成
別の FunctionApproximation.Problem オブジェクトを作成します。このオブジェクトの OnCurveTableValues プロパティを false に設定することで、最適化を有効にしてテーブル値およびブレークポイントを最適化します。
P2 = FunctionApproximation.Problem('tanh');
P2.Options.OnCurveTableValues = 0P2 =
1×1 FunctionApproximation.Problem with properties:
FunctionToApproximate: @(x)tanh(x)
NumberOfInputs: 1
InputTypes: "numerictype(1,16,12)"
InputLowerBounds: -8
InputUpperBounds: 8
OutputType: "numerictype(1,16,15)"
Options: [1×1 FunctionApproximation.Options]
ルックアップ テーブルによる近似を生成します。
S2 = solve(P2)
Searching for fixed-point solutions. | ID | Memory (bits) | Feasible | Table Size | Breakpoints WLs | TableData WL | BreakpointSpecification | Error(Max,Current) | | 0 | 64 | 0 | 2 | 16 | 16 | EvenSpacing | 7.812500e-03, 7.229091e-01 | | 1 | 1248 | 1 | 76 | 16 | 16 | EvenSpacing | 7.812500e-03, 4.368265e-03 | | 2 | 1232 | 1 | 75 | 16 | 16 | EvenSpacing | 7.812500e-03, 4.439035e-03 | | 3 | 944 | 1 | 57 | 16 | 16 | EvenSpacing | 7.812500e-03, 7.780470e-03 | | 4 | 928 | 1 | 56 | 16 | 16 | EvenSpacing | 7.812500e-03, 5.383741e-03 | | 5 | 656 | 0 | 39 | 16 | 16 | EvenSpacing | 7.812500e-03, 1.678519e-02 | | 6 | 640 | 0 | 38 | 16 | 16 | EvenSpacing | 7.812500e-03, 1.660649e-02 | | 7 | 784 | 1 | 47 | 16 | 16 | EvenSpacing | 7.812500e-03, 7.743777e-03 | | 8 | 704 | 1 | 42 | 16 | 16 | EvenSpacing | 7.812500e-03, 7.805676e-03 | | 9 | 672 | 1 | 40 | 16 | 16 | EvenSpacing | 7.812500e-03, 7.809550e-03 | | 10 | 368 | 0 | 21 | 16 | 16 | EvenSpacing | 7.812500e-03, 4.855583e-02 | | 11 | 512 | 0 | 30 | 16 | 16 | EvenSpacing | 7.812500e-03, 2.773526e-02 | | 12 | 592 | 0 | 35 | 16 | 16 | EvenSpacing | 7.812500e-03, 2.088471e-02 | | 13 | 624 | 0 | 37 | 16 | 16 | EvenSpacing | 7.812500e-03, 1.870074e-02 | | 14 | 384 | 1 | 12 | 16 | 16 | ExplicitValues | 7.812500e-03, 7.812317e-03 | | 15 | 384 | 0 | 12 | 16 | 16 | ExplicitValues | 7.812500e-03, 1.196141e-02 | | 16 | 384 | 1 | 12 | 16 | 16 | ExplicitValues | 7.812500e-03, 7.812317e-03 | Best Solution | ID | Memory (bits) | Feasible | Table Size | Breakpoints WLs | TableData WL | BreakpointSpecification | Error(Max,Current) | | 14 | 384 | 1 | 12 | 16 | 16 | ExplicitValues | 7.812500e-03, 7.812317e-03 |
S2 =
1×1 FunctionApproximation.LUTSolution with properties:
ID: 14
Feasible: "true"
結果の表示
各ルックアップ テーブルによる近似の最適解を比較します。
compare(S1)
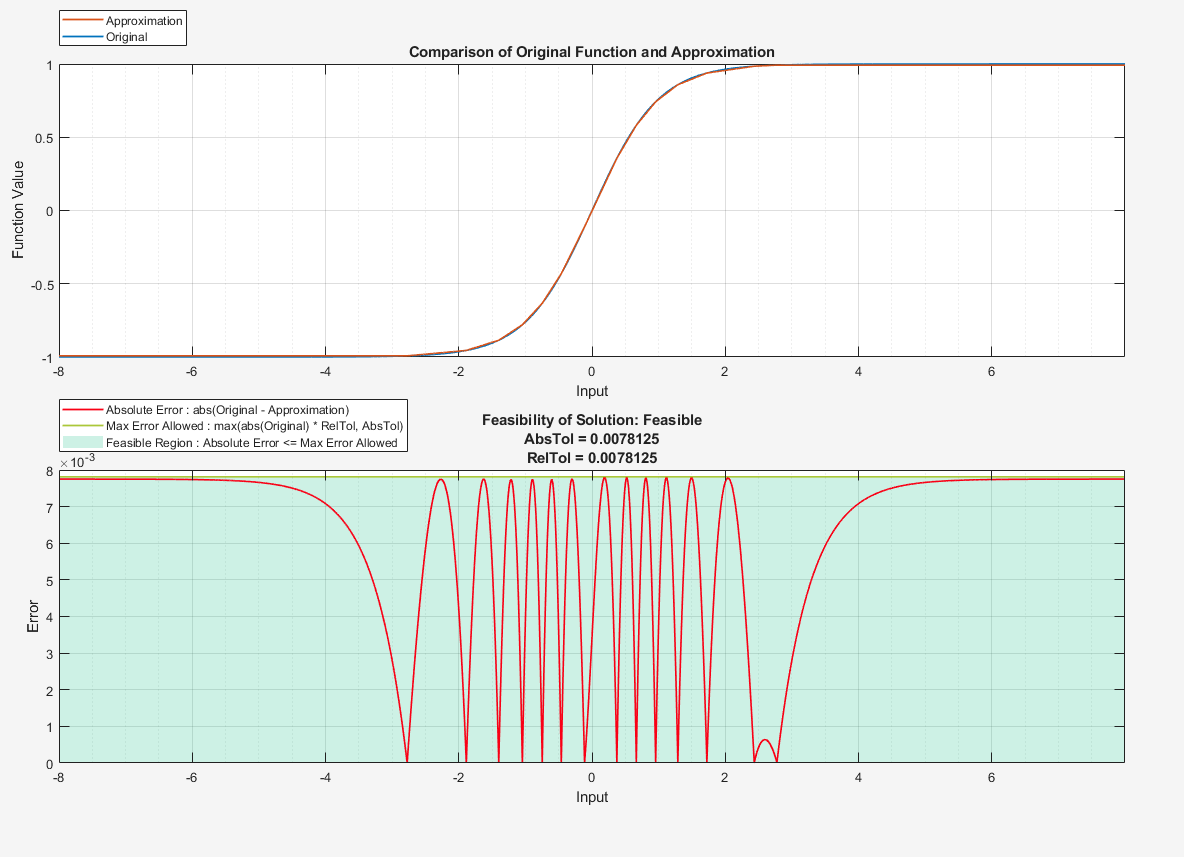
ans = struct with fields:
Breakpoints: [65536×1 double]
Original: [65536×1 double]
Approximate: [65536×1 double]
compare(S2)
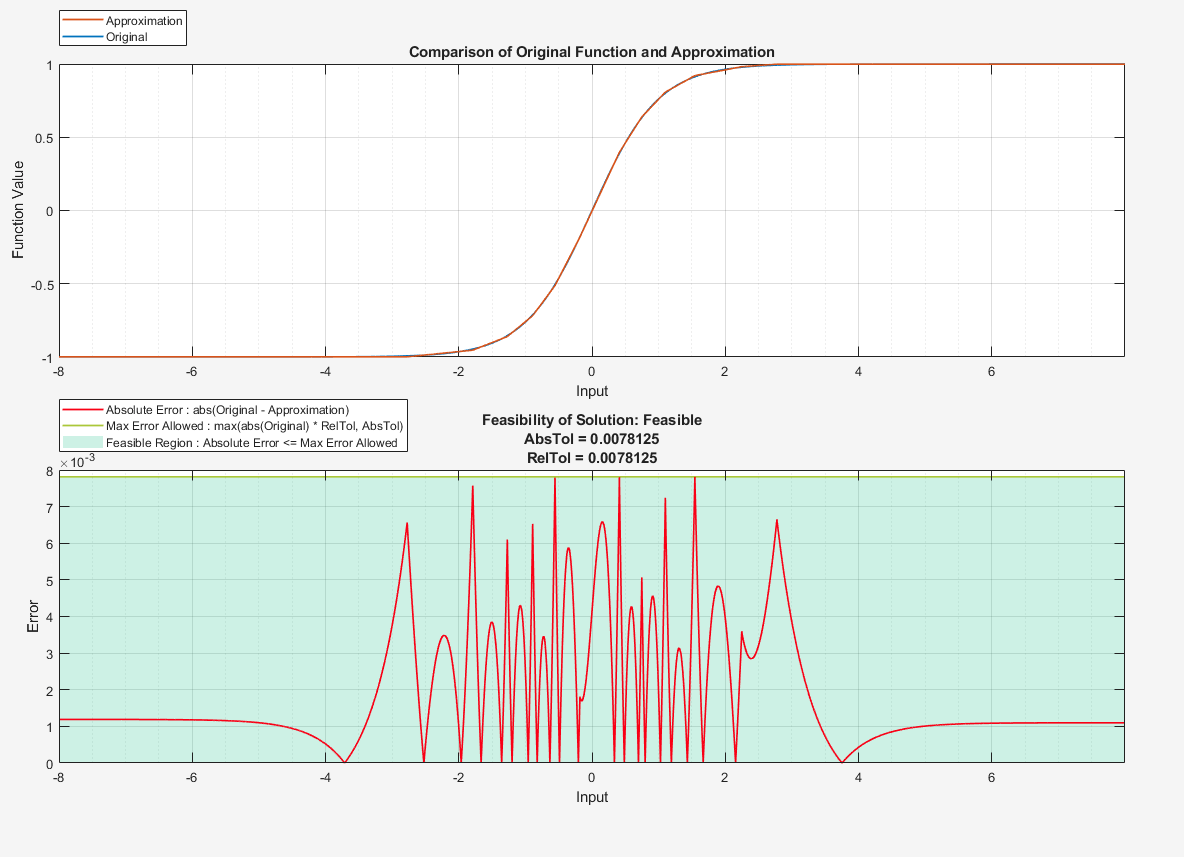
ans = struct with fields:
Breakpoints: [65536×1 double]
Original: [65536×1 double]
Approximate: [65536×1 double]
元の関数と 2 つのルックアップ テーブルによる近似の間の最大誤差はほぼ等しくなりますが、曲線上のテーブルの値のみを使用するよう制限されていなかったルックアップ テーブルが使用するメモリはかなり節約されます。
percent_reduction = S2.totalMemoryUsage/S1.totalMemoryUsage
percent_reduction = 0.8571
参考
アプリ
クラス
FunctionApproximation.Problem|FunctionApproximation.Options|FunctionApproximation.LUTSolution|FunctionApproximation.LUTMemoryUsageCalculator