FIR Halfband Interpolator

Interpolate signal using polyphase FIR half band filter

• 

Libraries:
DSP System Toolbox / Filtering / Multirate Filters

Description

The FIR Halfband Interpolator block performs interpolation of the input signal by a factor of two. The block uses an FIR equiripple design or a Kaiser window design to construct the halfband filters. The block uses an efficient polyphase implementation to filter the input. The implementation takes advantage of the zero-valued coefficients of the FIR halfband filter, making one of the polyphase branches a delay. For more information, see Algorithms. You can also use this block to implement the synthesis portion of a two-band filter bank to synthesize a signal from lowpass and highpass subbands.

The input signal can be a real- or complex-valued column vector or a matrix. If the input signal is a matrix, the block treats each column of the matrix as an independent channel. The block supports fixed-point operations and ARM^® Cortex^® code generation. For more information on ARM Cortex code generation, see Code Generation for ARM Cortex-M and ARM Cortex-A Processors.

The block also supports SIMD code generation. For details, see Code Generation.

Examples

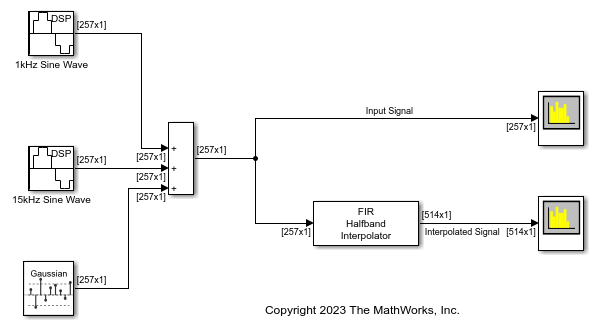
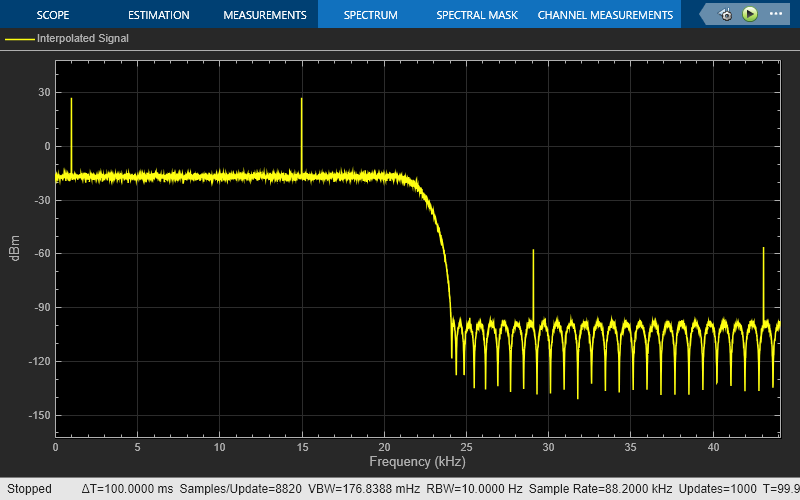
Design and Implement FIR Halfband Interpolator in Simulink

Design and implement an FIR halfband interpolator using the FIR Halfband Interpolator block. Pass a noisy input through the interpolator. Plot the spectrum of the input and the interpolated output in the spectrum analyzer.

Open and inspect the model. The input is a noisy sinusoidal signal with two frequencies, one at 1 kHz and the other at 15 kHz. Add white Gaussian noise with a mean of 0 and a variance of 0.05 to this signal.

The FIR halfband interpolator has a transition width of 4.1 kHz and a stopband attenuation of 80 dB. Visualize the magnitude response of the filter by clicking the View Filter Response button in the block dialog box.

Pass the noisy sinusoidal signal through the interpolator. Plot the spectrum of the input and the interpolated output in the spectrum analyzer.

Extract Low Frequency Subband From Speech in Simulink

Since R2023b

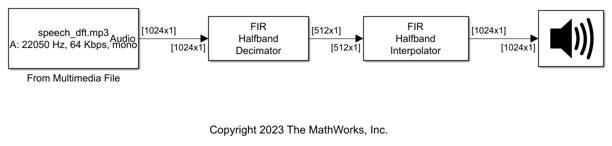
Use the FIR Halfband Decimator and FIR Halfband Interpolator blocks to extract and reconstruct the low-frequency subband from a speech signal.

Open and inspect the model. The input audio data is a single-channel speech signal with the sample rate of 22050 Hz.

Specify the Sample rate mode parameter of the FIR Halfband Decimator and FIR Halfband Interpolator blocks to Use normalized frequency (0 to 1). This option enables you to specify the transition width of the decimation and interpolation filters in normalized frequency units. Set the transition width to 0.093 in normalized frequency units and the stopband attenuation to 80 dB. The design method is set to Auto by default. In the Auto mode, the block selects the equiripple or Kaiser window design method based on the design parameters of the filter.

Read the speech signal from the audio file in frames of 1024 samples. The FIR Halfband Decimator block extracts and outputs the lowpass subband of the speech signal. The FIR Halfband Interpolator block reconstructs the lowpass approximation of the speech signal by interpolating the lowpass subband.

The Audio Device Writer block plays the filtered output.

Design and Implement Two-Channel FIR Filter Bank in Simulink

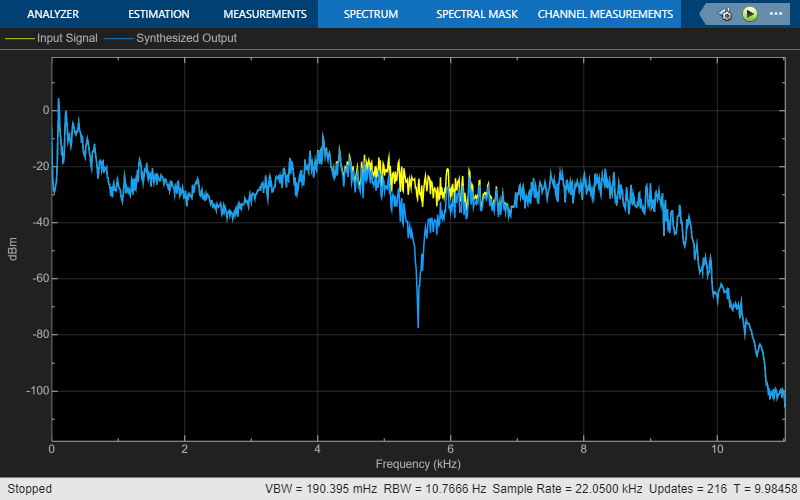
Use the FIR Halfband Decimator and FIR Halfband Interpolator blocks to implement a two-channel filter bank. This example uses an audio file input and shows that the power spectrum of the filter bank output does not differ significantly from the input. Play the output of the filter bank using the Audio Device Writer block.

Open and inspect the model. The input audio data is a single-channel speech signal with a sample rate of 22050 Hz.

The FIR Halfband Decimator block acts as an FIR halfband analysis bank as the Output highpass subband parameter is selected in the block dialog box. The FIR Halfband Interpolator block acts as an FIR halfband synthesis bank as the Input highpass subband parameter is selected in the block dialog box.

Set the Sample rate mode parameter in the FIR Halfband Decimator and FIR Halfband Interpolator blocks to Inherit from input port so that the blocks inherit the sample rate from the respective input ports. Set the transition width to 4.1 kHz and the stopband attenuation to 80 dB. The design method is set to Auto by default. In the Auto mode, the block selects the equiripple or Kaiser window design methods based on the design parameters of the filter.

Read the speech signal from the audio file in frames of 1024 samples. The FIR halfband analysis bank extracts the lowpass and highpass subbands of the speech signal. The FIR halfband synthesis filter bank synthesizes the speech signal from the lowpass and highpass subbands.

Display the power spectrum of the audio input and the output of the synthesis filter bank in the spectrum analyzer. Play the synthesized speech signal using the Audio Device Writer block.

Ports

Input

LP — Data input

column vector | matrix

Specify the data input as a vector or a matrix. If the input signal is a matrix, the block treats each column of the matrix as an independent channel.

When you select the Input highpass subband parameter, this block acts as a halfband synthesis filter bank. The input at this port is then the lowpass subband output of a halfband analysis filter bank.

This port is unnamed until you select the Input highpass subband parameter.

Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64 | fixed point
Complex Number Support: Yes

HP — Second input to the synthesis filter bank

column vector | matrix

Specify the second input to the synthesis filter bank as a column vector or a matrix. This signal is the highpass subband output of a halfband analysis filter bank. If the input signal is a matrix, the block treats each column of the matrix as an independent channel.

The size, data type, and complexity of both the inputs must be the same.

Dependency

To enable this port, select the Input highpass subband parameter.

Data Types: single | double | int8 | int16 | int32 | int64 | fixed point
Complex Number Support: Yes

Output

Output — Output of FIR halfband interpolator

column vector | matrix

Output of the FIR halfband interpolator, returned as a column vector or a matrix. The number of rows in the interpolator output is twice the number of rows in the input signal.

When the output is fixed-point, it is signed only.

Data Types: single | double | int8 | int16 | int32 | int64 | fixed point
Complex Number Support: Yes

Parameters

Main Tab

Filter specification — Filter design parameters

Transition width and stopband attenuation (default) | Filter order and transition width | Filter order and stopband attenuation | Coefficients

Select the parameters that the block uses to design the FIR halfband filter.

• Transition width and stopband attenuation (default) — Design the filter using Transition width (Hz) and Stopband attenuation (dB). This design is the minimum order design.

• Filter order and transition width — Design the filter using Filter order and Transition width (Hz).

• Filter order and stopband attenuation — Design the filter using Filter order and Stopband attenuation (dB).

• Coefficients — Specify the filter coefficients directly through the Numerator parameter.

Transition width (Hz) — Transition width in Hz

4.1e3 | positive real scalar

Specify the transition width as a real positive scalar in Hz or in normalized frequency units (since R2023b).

If you set the Sample rate mode parameter to:

• Specify on dialog or Inherit from input port –– The value of the transition width is in Hz and must be less than half the value of the output sample rate (2 × input sample rate).

• Use normalized frequency (0 to 1) –– The value of the transition width is in normalized frequency units. The value must be a positive scalar less than 1.0.

(since R2023b)

Dependencies

To enable this parameter, set Filter specification to Filter order and transition width or Transition width and stopband attenuation.

Filter order — Filter order

52 | even positive integer

Specify the filter order as an even positive integer.

Dependencies

To enable this parameter, set Filter specification to Filter order and transition width or Filter order and stopband attenuation.

Stopband attenuation (dB) — Stopband attenuation

80 (default) | positive real scalar

Specify the stopband attenuation as a real positive scalar in dB.

Dependencies

To enable this parameter, set Filter specification to Filter order and stopband attenuation or Transition width and stopband attenuation.

Numerator — FIR halfband filter coefficients

2*firhalfband("minorder",0.407,1e-4) (default) | row vector

Specify the FIR halfband filter coefficients directly as a row vector. The coefficients must comply with the FIR halfband impulse response format. If (length(Numerator) − 1)/2 is even, where (length(Numerator) − 1) is the filter order, every other coefficient starting with the first coefficient must be 0 except the center coefficient which must be 1.0. If (length(Numerator) − 1)/2 is odd, the sequence of alternating zeros with 1.0 at the center starts at the second coefficient.

Dependencies

To enable this parameter, set Filter specification to Coefficients.

Design method — Filter design method

Auto (default) | Equiripple | Kaiser

Specify the filter design method as one of the following:

• Auto –– The algorithm automatically chooses the filter design method depending on the filter design parameters. The algorithm uses the equiripple or the Kaiser window method to design the filter.

  If the design constraints are very tight, such as very high stopband attenuation or very narrow transition width, then the algorithm automatically chooses the Kaiser method, as this method is optimal for designing filters with very tight specifications. However, if the design constraints are not tight, then the algorithm chooses the equiripple method.

  When you set the Design method parameter to Auto, you can determine the method used by the algorithm by examining the passband and stopband ripple characteristics of the designed filter. If the block used the equiripple method, the passband and stopband ripples of the designed filter have a constant amplitude in the frequency response. If the filter design method the block chooses in the Auto mode is not suitable for your application, manually specify the Design method as Equiripple or Kaiser.

• Equiripple –– The algorithm uses the equiripple method.

• Kaiser –– The algorithm uses the Kaiser window method.

Dependencies

To enable this parameter, set Filter specification to Filter order and stopband attenuation, Filter order and transition width, or Transition width and stopband attenuation.

Input highpass subband — Input highpass subband

off (default) | on

When you select this check box, the block acts as a synthesis filter bank. The block accepts two inputs to synthesize: lowpass and highpass subbands. When you clear this check box, the block acts as an IIR half band interpolator and accepts a single vector or matrix as input. By default, this check box is cleared.

Sample rate mode — Mode to specify the input sample rate

Specify on dialog (default) | Inherit from input port | Use normalized frequency (0 to 1)

Since R2023b

Specify the input sample rate using one of these options:

• Specify on dialog –– Specify the input sample rate in the block dialog box using the Input sample rate (Hz) parameter.

• Inherit from input port –– The block inherits the sample rate from the input signal.

• Use normalized frequency (0 to 1) –– Specify the passband-edge and the stopband-edge frequencies in normalized frequency units (0 to 1).

Dependencies

To enable this parameter, set Filter specification to any value other than Coefficients.

Input sample rate (Hz) — Sample rate of input signal

44100 (default) | positive real scalar

Specify the sample rate of the input signal as a scalar in Hz.

Dependencies

To enable this parameter, set:

• Filter specification to any value other than Coefficients.

• Sample rate mode to Specify on dialog.

(since R2023b)

View Filter Response — View Filter Response

button

Click this button to open the Filter Visualization Tool (FVTool) and display the magnitude and phase response of the FIR Halfband Interpolator. The response is based on the values you specify in the block parameters dialog box. Changes made to these parameters update FVTool.

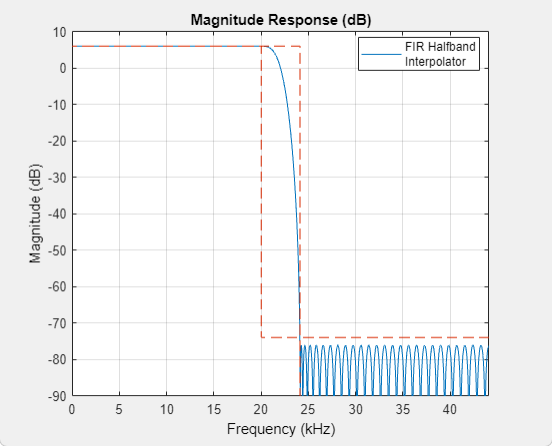
To update the magnitude response while FVTool is running, modify the dialog box parameters and click Apply.

Simulate using — Simulate using

Code generation (default) | Interpreted execution

Specify the type of simulation to run. You can set this parameter to:

• Code generation (default)

  Simulate model using generated C code. The first time you run a simulation, Simulink^® generates C code for the block. The C code is reused for subsequent simulations, as long as the model does not change. This option requires additional startup time but provides faster simulation speed than Interpreted execution.

• Interpreted execution

  Simulate model using the MATLAB^®  interpreter. This option shortens startup time but has slower simulation speed than Code generation.

Data Types Tab

Rounding mode — Rounding mode for output fixed-point operations

Floor (default) | Ceiling | Convergent | Nearest | Round | Simplest | Zero

Specify the rounding method for the output fixed-point operations. The rounding methods are Ceiling, Convergent, Floor, Nearest, Round, Simplest, and Zero. The default is Floor.

Coefficients — Word and fraction lengths of coefficients

fixdt(1,16) (default) | fixdt(1,16,0)

Specify the fixed-point data type of the coefficients as one of the following:

• fixdt(1,16) (default) — Signed fixed-point data type of word length 16 with binary point scaling. The block determines the fraction length automatically from the coefficient values in such a way that the coefficients occupy maximum representable range without overflowing.

• fixdt(1,16,0) — Signed fixed-point data type of word length 16 and fraction length, 0. You can change the fraction length to any other integer value.

• <data type expression> — Specify the coefficients data type by using an expression that evaluates to a data type object. For example, numerictype(fixdt([ ],18, 15)). Specify the sign mode of this data type as [ ] or true.

• Refresh Data Type — Refresh to the default data type.

Click the Show data type assistant button to display the data type assistant, which helps you set the coefficients data type.

Block Characteristics

Data Types	double | fixed point | single
Direct Feedthrough	no
Multidimensional Signals	no
Variable-Size Signals	yes
Zero-Crossing Detection	no

More About

Halfband Filters

An ideal lowpass halfband filter is given by

$$h(n)=\frac{1}{2\pi }{\displaystyle {\int }_{-\pi /2}^{\pi /2}{e}^{j\omega n}}d\omega =\frac{\sin (\frac{\pi }{2}n)}{\pi n}.$$

An ideal filter is not realizable because the impulse response is noncausal and not absolutely summable. However, the impulse response of an ideal lowpass filter possesses some important properties that are required in a realizable approximation. The impulse response of an ideal lowpass halfband filter is:

• Equal to 0 for all even-indexed samples

• Equal to 1/2 at n=0 as shown by L'Hôpital's rule on the continuous-valued equivalent of the discrete-time impulse response

The ideal highpass halfband filter is given by

$$g(n)=\frac{1}{2\pi }{\displaystyle {\int }_{-\pi }^{-\pi /2}{e}^{j\omega n}}d\omega +\frac{1}{2\pi }{\displaystyle {\int }_{\pi /2}^{\pi }{e}^{j\omega n}}d\omega .$$

Evaluating the preceding integral gives the following impulse response

$$g(n)=\frac{\sin (\pi n)}{\pi n}-\frac{\sin (\frac{\pi }{2}n)}{\pi n}.$$

The impulse response of an ideal highpass halfband filter is:

• Equal to 0 for all even-indexed samples

• Equal to 1/2 at n=0

The FIR halfband interpolator uses a causal FIR approximation to the ideal halfband response, which is based on minimizing the $${\ell }^{\infty }$$ norm of the error (minimax). See Algorithms for more information.

Kaiser Window

The coefficients of a Kaiser window are computed from this equation:

$$w(n)=\frac{I_0\left(\beta \sqrt{1-{\left(\frac{n-N/2}{N/2}\right)}^2}\right)}{I_0(\beta )},0\le n\le N,$$

where I₀ is the zeroth-order modified Bessel function of the first kind.

To obtain a Kaiser window that represents an FIR filter with stopband attenuation of α dB, use this β.

$$\beta =\{\begin{array}{ll}0.1102(\alpha -8.7),\hfill & \alpha >50\hfill \\ 0.5842{(\alpha -21)}^{0.4}+0.07886(\alpha -21),\hfill & 50\ge \alpha \ge 21\hfill \\ 0,\hfill & \alpha <21\hfill \end{array}$$

The filter order n is given by:

$$n=\frac{\alpha -7.95}{2.285(\Delta \omega )},$$

where Δω is the transition width.

Algorithms

Filter Design Method

The FIR halfband interpolator algorithm uses the equiripple or the Kaiser window method to design the FIR halfband filter. When the design constraints are tight, such as very high stopband attenuation or very narrow transition width, use the Kaiser window method. When the design constraints are not tight, use the equiripple method. If you are not sure of which method to use, set the design method to Auto. In this mode, the algorithm automatically chooses a design method that optimally meets the specified filter constraints.

Halfband Equiripple Design

In the equiripple method, the algorithm uses a minimax (minimize the maximum error) FIR design to design a fullband linear phase filter with the desired specifications. The algorithm upsamples a fullband filter to replace the even-indexed samples of the filter with zeros and creates a halfband filter. It then sets the filter tap corresponding to the group delay of the filter in samples to 1/2. This yields a causal linear-phase FIR filter approximation to the ideal halfband filter defined in Halfband Filters. See [1] for a description of this filter design method using the Remez exchange algorithm. Since you can design a filter using this approximation method with a constant ripple both in the passband and stopband, the filter is also known as the equiripple filter.

Kaiser Window Design

In the Kaiser window method, the algorithm first truncates the ideal halfband filter defined in Halfband Filters, then it applies a Kaiser window defined in Kaiser Window. This yields a causal linear-phase FIR filter approximation to the ideal halfband filter.

The coefficients of the designed halfband interpolation filter are scaled by the interpolation factor, two, to preserve the output power of the signal.

For more information on designing FIR halfband filters, see FIR Halfband Filter Design.

Polyphase Implementation with Halfband Filters

The FIR halfband interpolator uses an efficient polyphase implementation for halfband filters when you filter the input signal. You can use a polyphase implementation to move the upsampling operation after filtering. This allows you to filter at the lower sampling rate.

Splitting a filter’s impulse response h(n) into two polyphase components results in an even polyphase component with z-transform of

$$H_0(z)={\displaystyle \sum _{n}h}(2n)z^{-n},$$

and an odd polyphase component with z-transform of

$$H_1(z)={\displaystyle \sum _{n}h}(2n+1)z^{-n}.$$

The z-transform of the filter can be written in terms of the even and odd polyphase components as

$$H(z)=H_0(z^2)+z^{-1}{H}_1(z^2).$$

You can represent the upsampling by 2 and then filtering the signal using this figure.

Using the multirate noble identity for upsampling, you can move the upsampling operation after the filtering. This enables you to filter at the lower rate.

For a halfband filter, the only nonzero coefficient in the even polyphase component is the coefficient corresponding to z⁰. Implementing the halfband filter as a causal FIR filter shifts the nonzero coefficient to approximately z^-N/4, where N is the number of filter taps. This process is shown in the following figure. The top plot shows a halfband filter of order 52. The bottom plot shows the even polyphase component. Both filters are noncausal. Delaying the even polyphase component by 13 samples creates a causal FIR filter.

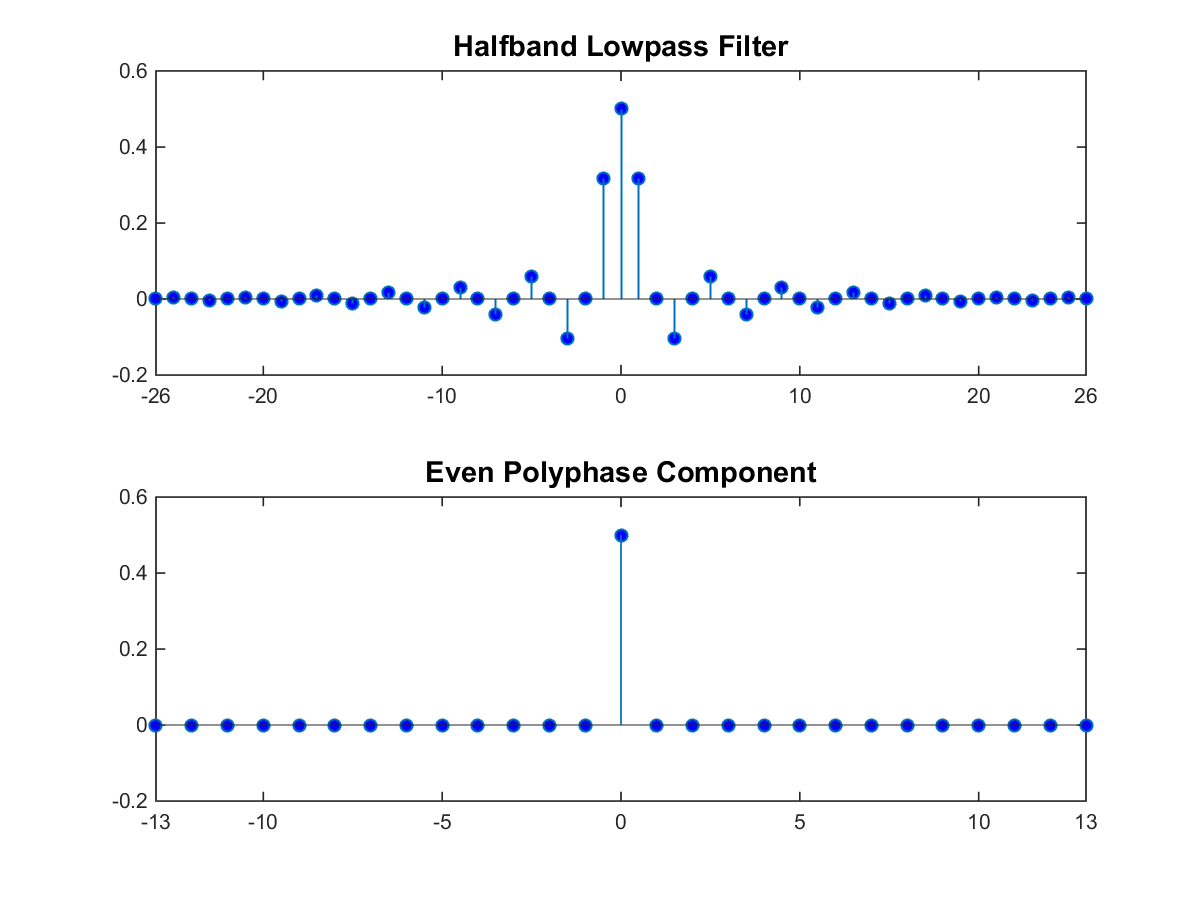
To efficiently implement the halfband interpolator, the algorithm replaces the upsampling operator, delay block, and adder with a commutator switch. The commutator switch starts on the even branch and takes input samples from the two branches alternately, one sample at a time. This doubles the sampling rate of the input signal. Which polyphase component reduces to a simple delay depends on whether the half order of the filter is even or odd.

Here is the implementation when the filter half order is even. In this diagram, H₀(z) becomes the gain followed by the delay.

When the filter half order is odd, H₁(z) becomes the gain followed by the delay and the switch. This is because the delay required to make the even polyphase component causal can be odd or even depending on the filter half order.

To confirm this behavior, run the following code in the MATLAB command prompt and inspect the polyphase components of the following filters.

filterspec = "Filter order and stopband attenuation";
halfOrderEven = dsp.FIRHalfbandInterpolator(Specification=filterspec,...
    FilterOrder=64,StopbandAttenuation=80);
halfOrderOdd = dsp.FIRHalfbandInterpolator(Specification=filterspec,...
    FilterOrder=54,StopbandAttenuation=80);
polyphase(halfOrderEven)
polyphase(halfOrderOdd)

One of the polyphase components has a single nonzero coefficient indicating that it is a simple delay. To preserve the output power of the signal, the coefficients are scaled by the interpolation factor, two. To see this scaling, compare the polyphase components of a halfband interpolator with the coefficients of a halfband decimator.

hfirinterp = dsp.FIRHalfbandInterpolator;
hfirdecim = dsp.FIRHalfbandDecimator;
polyphase(hfirdecim)
polyphase(hfirinterp)

Synthesis Filter Bank

The FIR halfband interpolator implements the synthesis portion of a two-band filter bank to synthesize a signal from lowpass and highpass subbands.

For more information on filter banks, see Overview of Filter Banks.

To summarize, the FIR halfband interpolator:

• Filters the input before upsampling with the even and odd polyphase components of the filter.

• Exploits the fact that one filter polyphase component is a simple delay for a halfband filter.

• Acts as a synthesis filter bank.

Extended Capabilities

C/C++ Code Generation

Generate C and C++ code using Simulink® Coder™.

The FIR Halfband Interpolator block supports SIMD code generation using Intel AVX2 code replacement library when the data type of the input signal is single or double.

The SIMD technology significantly improves the performance of the generated code. For more information, see SIMD Code Generation. To generate SIMD code from this block, see Use Intel AVX2 Code Replacement Library to Generate SIMD Code from Simulink Blocks.

Fixed-Point Conversion
Design and simulate fixed-point systems using Fixed-Point Designer™.

Version History

Introduced in R2015b

R2023b: Support for normalized frequencies

When you set the Sample rate mode parameter to Use normalized frequency (0 to 1), you can specify the transition width in normalized frequency units (0 to 1).