designMultirateFIR
Design and implement antialiasing and anti-imaging lowpass FIR filter
Description
B = designMultirateFIRB is a vector of filter
coefficients. To implement the filter, you must assign the filter coefficients
B to a multirate filter object.
The multirate FIR filter is an antialiasing and anti-imaging lowpass FIR filter used in digital rate conversion.
B = designMultirateFIR(Name=Value)
For example, B =
designMultirateFIR(InterpolationFactor=3,DecimationFactor=2,SystemObject=true)SystemObject argument is true, the
function returns a dsp.FIRRateConverter
System object™.
When you specify only a partial list of filter parameters, the function designs the filter by setting the other design parameters to their default values.
When you specify any of the numeric input arguments in single precision, the
function designs the filter coefficients in single precision. Alternatively, you can use the Datatype
and like arguments to control the data type of the
coefficients. (since R2024b)
Examples
To design an FIR interpolator using the designMultirateFIR function, specify the interpolation factor (usually a value greater than 1) and set the decimation factor to 1. You can use the default polyphase length and stopband attenuation or you can use nondefault values.
Design an FIR interpolator with the interpolation factor of 5. Use the default polyphase length of 24 and the default stopband attenuation of 80 dB.
b = designMultirateFIR(InterpolationFactor=5,DecimationFactor=1); impz(b)

Design a polyphase FIR interpolator by using the designMultirateFIR function with the interpolation factor of 5, normalized transition width of 0.01, and stopband attenuation of 60 dB. Set the 'SystemObject' argument to true to create a dsp.FIRInterpolator object. To design the filter in single-precision, use the Datatype or like argument. Alternatively, you can specify any of the numerical arguments in single-precision.
firInterp = designMultirateFIR(InterpolationFactor=5,... TransitionWidth=0.01,... StopbandAttenuation=60,... Datatype="single",... SystemObject=true,... Verbose=true)
designMultirateFIR(InterpolationFactor=5, DecimationFactor=1, TransitionWidth=0.01, InputSampleRate="normalized", OverlapTransition=true, DesignMethod="kaiser", StopbandAttenuation=60, Datatype="single", SystemObject=true)
firInterp =
dsp.FIRInterpolator with properties:
InterpolationFactor: 5
NumeratorSource: 'Property'
Numerator: [8.5015e-05 8.9039e-05 5.7574e-05 0 -6.2845e-05 -1.0610e-04 -1.1061e-04 -7.1214e-05 0 7.7112e-05 1.2970e-04 1.3474e-04 8.6452e-05 0 -9.3019e-05 -1.5599e-04 -1.6159e-04 -1.0340e-04 0 1.1067e-04 1.8515e-04 … ] (1×727 single)
Show all properties
Visualize the magnitude and phase response of the FIR interpolator using the freqzmr function. The response curves show the magnitude and phase responses of a linearly interpolated filter.
freqzmr(firInterp)

Compute the cost of implementing the filter.
cost(firInterp)
ans = struct with fields:
NumCoefficients: 582
NumStates: 145
MultiplicationsPerInputSample: 582
AdditionsPerInputSample: 578
Measure the frequency response characteristics of the filter object.
measure(firInterp)
ans = Sample Rate : N/A (normalized frequency) Passband Edge : 0.195 3-dB Point : 0.19884 6-dB Point : 0.2 Stopband Edge : 0.205 Passband Ripple : 0.016474 dB Stopband Atten. : 60.183 dB Transition Width : 0.01
Design a polyphase FIR interpolator using the "lagrange" design method with the interpolation factor of 5. To use the zero-order hold method, set the polyphase length to 1.
P = 1; firInterpLagrange = designMultirateFIR(InterpolationFactor=5,... DesignMethod='lagrange',PolyphaseLength=P,... SystemObject=true)
firInterpLagrange =
dsp.FIRInterpolator with properties:
InterpolationFactor: 5
NumeratorSource: 'Property'
Numerator: [1 1 1 1 1]
Show all properties
Pass the sinusoidal input signal to the FIR interpolation filter.
u = sin(2*pi*(0:7)/8)'; y = firInterpLagrange(u);
To plot the input and output signals of the FIR interpolation filter on the same plot, you need to account for the output delay of the filter. To compute the output delay, use the outputDelay function.
[D,FsOut] = outputDelay(firInterpLagrange)
D = 0.4000
FsOut = 5
Initialize the timescope object. Update the TimeDisplayOffet property with the output delay of the filter. Visualize the input and output signals on the time scope.
ts = timescope(NumInputPorts=2,SampleRate=[FsOut 1],... TimeDisplayOffset=[0, D],... ChannelNames={"Output","Input"}, ... TimeSpan=length(u)*1.1, ... YLimits=[-1.1,1.1],... PlotType="stem"); ts(y,u)

Design an FIR decimator with the decimation factor of 3 and polyphase length of 28. Use the default stopband attenuation of 80 dB.
b = designMultirateFIR(InterpolationFactor=1,... DecimationFactor=3,... PolyphaseLength=28); impz(b)

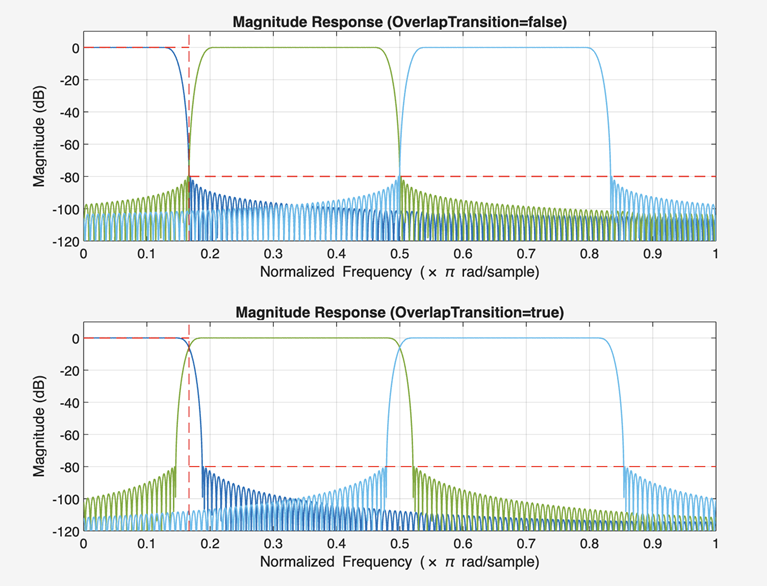
Create a dsp.FIRDecimator object by setting the SystemObject flag to true. This design has the OverlapTransition set to true by default. The transition bands therefore overlap.
bSysObjwithOverlap = designMultirateFIR(InterpolationFactor=1,... DecimationFactor=3,... PolyphaseLength=28,SystemObject=true,... Verbose=true)
designMultirateFIR(InterpolationFactor=1, DecimationFactor=3, PolyphaseLength=28, InputSampleRate="normalized", OverlapTransition=true, DesignMethod="kaiser", StopbandAttenuation=80, Datatype="double", SystemObject=true)
bSysObjwithOverlap =
dsp.FIRDecimator with properties:
Main
DecimationFactor: 3
NumeratorSource: 'Property'
Numerator: [0 -3.3618e-05 -5.6028e-05 0 1.2589e-04 1.7681e-04 0 -3.2083e-04 -4.1865e-04 0 6.7942e-04 8.4848e-04 0 -0.0013 -0.0016 0 0.0022 0.0026 0 -0.0036 -0.0043 0 0.0057 0.0066 0 -0.0087 -0.0099 0 0.0130 0.0148 0 -0.0194 … ] (1×84 double)
Structure: 'Direct form'
Show all properties
Set the OverlapTransition to false and redesign the FIR decimator.
bSysObjwithNoOverlap = designMultirateFIR(InterpolationFactor=1,... DecimationFactor=3,... PolyphaseLength=28,SystemObject=true,... OverlapTransition=false,Verbose=true)
designMultirateFIR(InterpolationFactor=1, DecimationFactor=3, PolyphaseLength=28, InputSampleRate="normalized", OverlapTransition=false, DesignMethod="kaiser", StopbandAttenuation=80, Datatype="double", SystemObject=true)
bSysObjwithNoOverlap =
dsp.FIRDecimator with properties:
Main
DecimationFactor: 3
NumeratorSource: 'Property'
Numerator: [-1.7738e-05 -2.1857e-05 1.0313e-05 7.8283e-05 1.2681e-04 7.1241e-05 -1.1841e-04 -3.3767e-04 -3.7033e-04 -5.2466e-05 5.1928e-04 9.3352e-04 7.0375e-04 -2.9223e-04 -0.0015 -0.0020 -8.6943e-04 0.0014 0.0034 0.0033 … ] (1×85 double)
Structure: 'Direct form'
Show all properties
Visualize the magnitude response of the two designs using freqzmr. The design with overlap shows distortion at higher frequencies.
freqzmr(bSysObjwithOverlap)
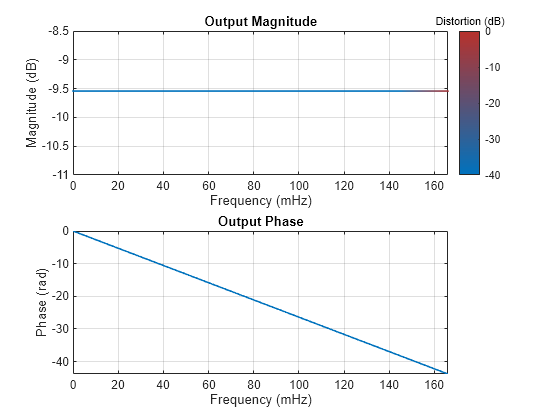
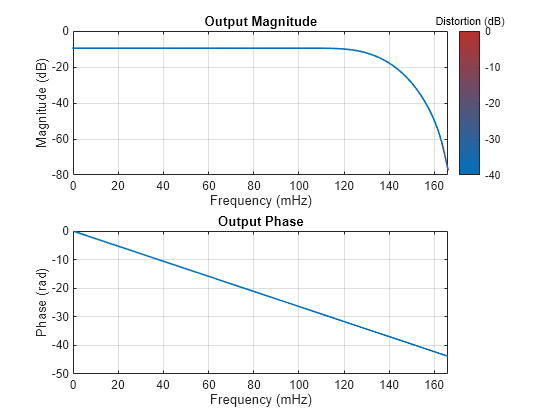
The design with no overlap has no aliasing or imaging issues at the higher frequencies.
freqzmr(bSysObjwithNoOverlap)
Design an FIR rate converter with the interpolation factor of 3, decimation factor of 4, polyphase length of 28, and stopband attenuation of 90 dB. Use the Datatype argument to design the filter in single-precision.
L = 3; M = 4; PL = 28; Ast = 90; b = designMultirateFIR(InterpolationFactor=L,... DecimationFactor=M,... PolyphaseLength=PL,... StopbandAttenuation=Ast,... Datatype="single"); impz(b,1)

Design an FIR rate converter with the interpolation factor of 3, decimation factor of 4, normalized transition width of 0.2, and stopband attenuation of 90 dB. Use the like argument to design the filter in single-precision.
TW = 0.2; bTW = designMultirateFIR(InterpolationFactor=L,... DecimationFactor=M,... TransitionWidth=TW,... StopbandAttenuation=Ast,... like=single(M)); impz(bTW,1)

Since R2024b
Design an FIR rate converter using the Kaiser window design method. The design has nonoverlapping transition bands. Compare the design containing a polyphase length of 40 with a design of polyphase length 80.
Use the designMultirateFIR function to design the two rate conversion filters.
Set
DecimationFactorto 9Set
InterpolationFactorto 5Set
DesignMethodto"kaiser"Set
OverlapTransitiontofalse.Set
PolyphaseLengthto 40 and 80, respectively, for the two filters.Set
InputSampleRateto 1200 Hz.
rcPoly40 = designMultirateFIR(DecimationFactor=9,... InterpolationFactor=5,OverlapTransition=false,... PolyphaseLength=40,InputSampleRate=1200,... Verbose=true,SystemObject=true)
designMultirateFIR(InterpolationFactor=5, DecimationFactor=9, PolyphaseLength=40, InputSampleRate=1200, OverlapTransition=false, DesignMethod="kaiser", StopbandAttenuation=80, Datatype="double", SystemObject=true)
rcPoly40 =
dsp.FIRRateConverter with properties:
Main
InterpolationFactor: 5
DecimationFactor: 9
NumeratorSource: 'Property'
Numerator: [3.5638e-05 5.0900e-05 6.5026e-05 7.4794e-05 7.6537e-05 6.6569e-05 4.1705e-05 -1.3935e-07 -5.9359e-05 -1.3414e-04 -2.2010e-04 -3.1017e-04 -3.9481e-04 -4.6249e-04 -5.0064e-04 -4.9684e-04 -4.4025e-04 -3.2327e-04 … ] (1×201 double)
Show all properties
rcPoly80 = designMultirateFIR(DecimationFactor=9,... InterpolationFactor=5,OverlapTransition=false,... PolyphaseLength=80,InputSampleRate=1200,... Verbose=true,SystemObject=true)
designMultirateFIR(InterpolationFactor=5, DecimationFactor=9, PolyphaseLength=80, InputSampleRate=1200, OverlapTransition=false, DesignMethod="kaiser", StopbandAttenuation=80, Datatype="double", SystemObject=true)
rcPoly80 =
dsp.FIRRateConverter with properties:
Main
InterpolationFactor: 5
DecimationFactor: 9
NumeratorSource: 'Property'
Numerator: [-1.5627e-05 -2.1798e-05 -2.6892e-05 -2.9819e-05 -2.9550e-05 -2.5283e-05 -1.6599e-05 -3.6000e-06 1.3008e-05 3.1892e-05 5.1155e-05 6.8479e-05 8.1348e-05 8.7337e-05 8.4428e-05 7.1331e-05 4.7765e-05 1.4649e-05 … ] (1×401 double)
Show all properties
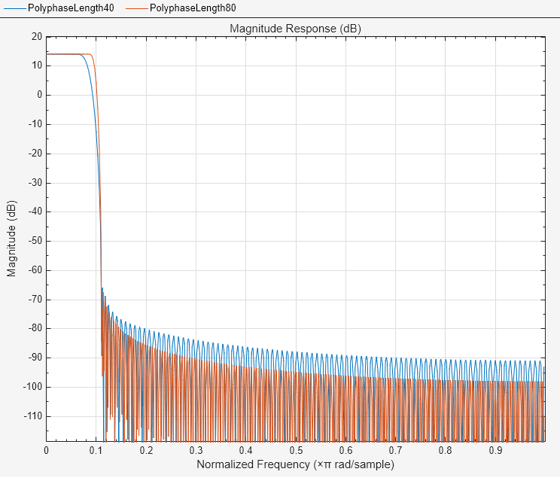
Visualize the magnitude response of these two filters. The filter with the longer polyphase length has a narrower transition width. The stopband edge for both filters is exactly 1/max(9,5) or 1/9.
filterAnalyzer(rcPoly40,rcPoly80,FilterNames=["PolyphaseLength40","PolyphaseLength80"])
Since R2024b
Design FIR rate converter that converts a signal from 44.1 kHz to 48 kHz with a polyphase length of 24. Design the filter with both the Kaiser method and equiripple method. Compare the two designs.
Use the designMultirateFIR function to design the two filters.
Set
InterpolationFactorto 160.Set
DecimationFactorto 147.Set
OverlapTransitiontofalseso that the two filters have nonoverlapping transition bands.Set
PolyphaseLengthto 24.Set
DesignMethodto"equiripple"and"kaiser", respectively, for the two filters.
L = 160; M = 147; rcEqui = designMultirateFIR(DecimationFactor=M,... InterpolationFactor=L,OverlapTransition=false,... PolyphaseLength=24, DesignMethod='equiripple',Systemobject=true)
rcEqui =
dsp.FIRRateConverter with properties:
Main
InterpolationFactor: 160
DecimationFactor: 147
NumeratorSource: 'Property'
Numerator: [-0.0081 -1.7231e-04 -1.7393e-04 -1.7543e-04 -1.7679e-04 -1.7802e-04 -1.7911e-04 -1.8005e-04 -1.8085e-04 -1.8151e-04 -1.8201e-04 -1.8235e-04 -1.8254e-04 -1.8257e-04 -1.8243e-04 -1.8213e-04 -1.8166e-04 … ] (1×3840 double)
Show all properties
rcKaiser = designMultirateFIR(DecimationFactor=M,... InterpolationFactor=L, OverlapTransition=false,... PolyphaseLength=24, DesignMethod='kaiser',Systemobject=true)
rcKaiser =
dsp.FIRRateConverter with properties:
Main
InterpolationFactor: 160
DecimationFactor: 147
NumeratorSource: 'Property'
Numerator: [-7.0937e-05 -7.2078e-05 -7.3209e-05 -7.4331e-05 -7.5442e-05 -7.6541e-05 -7.7628e-05 -7.8701e-05 -7.9760e-05 -8.0804e-05 -8.1832e-05 -8.2843e-05 -8.3836e-05 -8.4811e-05 -8.5766e-05 -8.6701e-05 -8.7614e-05 … ] (1×3841 double)
Show all properties
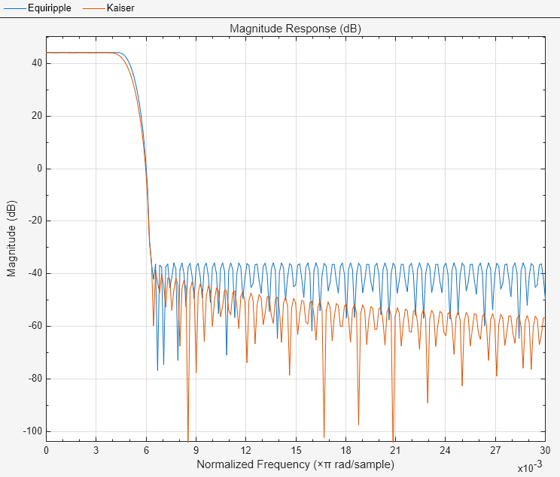
Compare the magnitude response of the two designs. The equiripple design performs slightly better in the transition band at the expense of a nearly negligible passband ripple.
fa = filterAnalyzer(rcEqui,rcKaiser,FilterNames=["Equiripple","Kaiser"]); zoom(fa,"x",[0 0.03])
Since R2024b
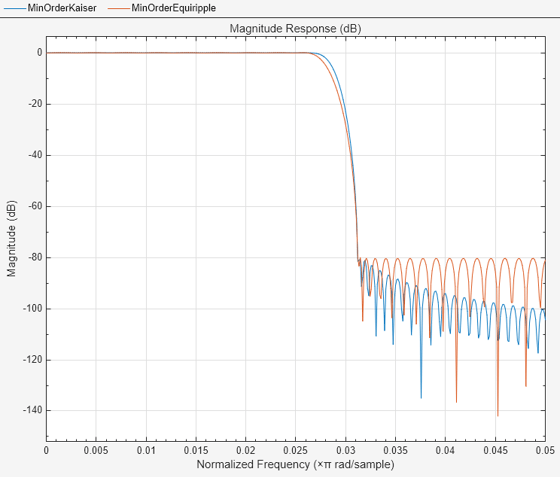
Design a minimum-order FIR decimator from 32 kHz to 1 kHz with a transition width of 0.005. Compare the Kaiser design with the equiripple design.
Use the designMultirateFIR function to design two FIR decimators, one with the Kaiser design and the other with the equiripple design. Set the decimation factor to 32, OverlapTransition to false, and the transition width to 0.005. The interpolation factor is 1 by default.
M = 32; Tw = 0.005; minOrderKaiser = designMultirateFIR(DecimationFactor=M,... OverlapTransition=false,TransitionWidth=Tw,... DesignMethod='kaiser',SystemObject=true,... Verbose=true)
designMultirateFIR(InterpolationFactor=1, DecimationFactor=32, TransitionWidth=0.005, InputSampleRate="normalized", OverlapTransition=false, DesignMethod="kaiser", StopbandAttenuation=80, Datatype="double", SystemObject=true)
minOrderKaiser =
dsp.FIRDecimator with properties:
Main
DecimationFactor: 32
NumeratorSource: 'Property'
Numerator: [3.4905e-07 4.3070e-07 5.1335e-07 5.9619e-07 6.7836e-07 7.5896e-07 8.3709e-07 9.1179e-07 9.8213e-07 1.0471e-06 1.1059e-06 1.1574e-06 1.2009e-06 1.2354e-06 1.2602e-06 1.2744e-06 1.2775e-06 1.2689e-06 1.2479e-06 … ] (1×2009 double)
Structure: 'Direct form'
Show all properties
minOrderEquiripple = designMultirateFIR(DecimationFactor=M,... OverlapTransition=false,TransitionWidth=Tw,... DesignMethod='equiripple',SystemObject=true,... Verbose=true)
designMultirateFIR(InterpolationFactor=1, DecimationFactor=32, TransitionWidth=0.005, InputSampleRate="normalized", OverlapTransition=false, DesignMethod="equiripple", StopbandAttenuation=80, PassbandRipple=0.1, Datatype="double", SystemObject=true)
minOrderEquiripple =
dsp.FIRDecimator with properties:
Main
DecimationFactor: 32
NumeratorSource: 'Property'
Numerator: [5.2919e-05 1.1057e-05 1.2117e-05 1.3176e-05 1.4225e-05 1.5254e-05 1.6252e-05 1.7210e-05 1.8113e-05 1.8950e-05 1.9707e-05 2.0371e-05 2.0927e-05 2.1366e-05 2.1675e-05 2.1844e-05 2.1862e-05 2.1719e-05 2.1399e-05 … ] (1×1377 double)
Structure: 'Direct form'
Show all properties
Compare the magnitude response of the two designs. The Kaiser design performs better in the transition width compared to the equiripple design.
fa = filterAnalyzer(minOrderKaiser,minOrderEquiripple,... FilterNames=["MinOrderKaiser","MinOrderEquiripple"]); zoom(fa,"x",[0 0.05])
Name-Value Arguments
Specify optional pairs of arguments as
Name1=Value1,...,NameN=ValueN, where Name is
the argument name and Value is the corresponding value.
Name-value arguments must appear after other arguments, but the order of the
pairs does not matter.
Example: designMultirateFIR(InterpolationFactor=3,PolyphaseLength=32,SystemObject=true)
designs and returns a dsp.FIRInterpolator object with an
interpolation factor of 3.
Interpolation factor L, specified as a positive integer. To design a pure decimator, set L to 1.
If you design the filter using PolyphaseLength,
the interpolation factor is tunable in the generated code, that is, you
can pass the interpolation factor as a runtime variable while generating
code.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Decimation factor M, specified as a positive
integer. To design a pure interpolator, set M to
1.
If you design the filter using PolyphaseLength,
the decimation factor is tunable in the generated code, that is, you can
pass the decimation factor as a runtime variable while generating
code.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Polyphase length P, specified as one of these:
1–– SetDesignMethodto"lagrange". The function uses the zero-order hold method.2–– The function accepts all the design methods. If you setDesignMethodto"lagrange", then 2 is the default polyphase length and the function uses the linear interpolation method.Positive even integer > 2 –– Set
DesignMethodto"kaiser"or"equiripple".
The polyphase length is tunable in generated code, that is, you can pass the polyphase length as a runtime variable while generating code.
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Since R2024b
Control the transition band overlap, specified as one of these values:
true–– The transition band of aliases or images overlap. You can use only the Kaiser-window-based design method or the Lagrange polynomial method.false–– The transition bands do not overlap and this property reduces aliasing at higher frequencies. The stopband edge starts exactly at 1/max(L,M) and the entire transition band is contained completely below the stopband edge frequency. L is the interpolation factor and M is the decimation factor. This option allows you to use the equiripple design.
Data Types: logical
Since R2024b
Design method for the lowpass FIR filter, specified as one of these:
"kaiser"–– Kaiser-window-based design. The function uses this method by default if you setOverlapTransitiontotrue."equiripple"–– Equiripple design method. The function supports this method only when you setOverlapTransitiontofalse."lagrange"–– Lagrange polynomial method. To use this method, set:PolyphaseLengthto 1 (zero-order hold) or 2 (linear interpolation).OverlapTransitiontotrue.
(since R2025a)
When you set DesignMethod to
"kaiser" or "equiripple",
specifying both the transition width and polyphase length results in an
overdetermined design. The function does not support specifying both the
values.
For more information on the design methods, see Algorithms.
Data Types: char | string
Transition width, TW, of the multirate FIR filter, specified as one of these:
Normalized scalar in the range (0,1) when you set
InputSampleRate, FsIn, to"normalized".When you set
OverlapTransitiontotrue, the value of the transition width must be less than or equal to 2/max(L,M), where L is the interpolation factor and M is the decimation factor.When you set
OverlapTransitiontofalse, the value of the transition width must be less than or equal to 1/max(L,M).
Positive scalar in Hz when you set
InputSampleRate, FsIn, to a positive scalar in Hz. (since R2025a)When you set
OverlapTransitiontotrue, the value of the transition width must be less than or equal to FsIn×min(1,L/M).When you set
OverlapTransitiontofalse, the value of the transition width must be less than or equal to FsIn×min(1,L/M)/2.
Specifying both transition width and polyphase length results in an overdetermined design. The function does not support specifying both the values. When you use the transition width to design the filter, the function determines the polyphase length (and therefore the filter length) iteratively.
If you set
DesignMethod to "lagrange",
you cannot set this argument. (since R2025a)
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Since R2025a
Sample rate of the filter input, FsIn, specified as one of these options:
"normalized"when frequency specifications such as the transition width are in the normalized frequency units (0,1). Filter analysis tools such as thefilterAnalyzeranalyze the filter in normalized frequency units.Positive scalar when frequency specifications such as the transition width are specified in Hz. Filter analysis tools use this value to analyze the filter.
Data Types: single | double | char | string
Stopband attenuation in dB, specified as a nonnegative real scalar greater than or equal to 0.
The function applies the default stopband attenuation value of 80 dB only when you set the interpolation factor L or the decimation factor M to a value greater than 1.
If you design the filter using PolyphaseLength,
the stopband attenuation is tunable in the generated code, that is, you
can pass the stopband attenuation as a runtime variable while generating
code.
If you set
DesignMethod to "lagrange",
you cannot set this argument. (since R2025a)
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Since R2024b
Passband ripple, specified as a positive scalar.
Dependencies
This property applies only when you set
DesignMethod to
"equiripple".
Data Types: single | double | int8 | int16 | int32 | int64 | uint8 | uint16 | uint32 | uint64
Since R2024b
Data type of the filter coefficients by type name, specified as
"double" or
"single".
You can use the Dataype or the
like argument to specify the
data type of the filter coefficients, but you cannot use both
arguments at the same time.
If you specify the data type of the filter coefficients using this argument, the function ignores the data types of the other numeric arguments.
Data Types: char | string
Since R2024b
Data type of the filter coefficients as a prototype, specified as a real floating-point value.
You can use the Dataype or the
like argument to specify the data type of
filter coefficients, but you cannot use both arguments at the same
time.
If you specify the data type of the filter coefficients using this argument, the function ignores the data types of the other numeric arguments.
Example: B =
designMultirateFIR(InterpolationFactor=L,DecimationFactor=M,like=single(M))
Example: M = single(5); B =
designMultirateFIR(InterpolationFactor=L,DecimationFactor=M,like=M)
Data Types: single | double
Option to create a multirate filter System object, specified as one of these:
false–– The function returns a vector of multirate FIR filter coefficients.true–– The function returns one of these System objects:dsp.FIRInterpolatorwhenL≥ 1 andM= 1dsp.FIRDecimatorwhenL= 1 andM> 1dsp.FIRRateConverterwhenL> 1 andM> 1
When you set the
SystemObjectproperty totrue, the function now factors out the GCD in the rate conversion ratio L:M. For example, the function treats an L:M ratio of 8:4 as 2:1. With this change, these two function calls have the same output.(since R2025a)designMultirateFIR(InterpolationFactor=12,DecimationFactor=40,... SystemObject=true) designMultirateFIR(InterpolationFactor=3,DecimationFactor=10,... SystemObject=true)
Data Types: logical
Option to print the entire function call in MATLAB, specified as one of these:
false–– The function does not print the function call.true–– The function prints the entire function call including the default values of theName=Valuearguments that you did not specify when calling the function.Use this argument to view all the values used by the function to design and implement the filter.
Data Types: logical
Output Arguments
Designed filter, returned as one of these options.
Multirate FIR filter coefficients –– The function returns a row vector of length N when you set the
SystemObjectargument tofalse.If both L and M are equal to 1, N = 1.
If L > 1 or M > 1, , where 2P is the polyphase length and R is defined by one of these equations:
R = L if L > 1
R = M if L = 1.
For more details, see the Algorithms section.
If you specify single-precision values in any of the input arguments, the function outputs single-precision filter coefficients. (since R2024a)
If you specify the data type using the
Datatypeor thelikeargument, the function ignores the data types of the other numeric arguments. (since R2024b)Multirate FIR filter object –– The function returns one of these multirate filter System objects when you set the
SystemObjectargument totrue.dsp.FIRInterpolatorwhenL> 1 andM= 1.dsp.FIRDecimatorwhenL= 1 andM> 1.dsp.FIRRateConverterwhenL> 1 andM> 1.
Data Types: single | double
Algorithms
OverlapTransition to truedesignMultirateFIR designs an
Rth band Nyquist FIR filter
using a Kaiser window vector to window the truncated impulse response of the FIR
filter.
The filter length N is defined as
where, P is the polyphase length and R is the number of polyphase branches which is defined by one of these equations:
R = L if L > 1
R = M if L = 1.
The function algorithm delays the truncated impulse response d(n) by N/2 samples to make it causal. The truncated and delayed impulse response is
where .
For every Rth band, the impulse response of the Nyquist filters is exactly zero. Because of this property, when the algorithm uses Nyquist filters for pure interpolation, the input samples remain unaltered after interpolating.
When designing a Nyquist filter, the algorithm uses a Kaiser window because of its near-optimum performance and ability to provide a robust design. The window depends on two parameters: length N + 1 and shape parameter β.
The Kaiser window is defined by
where I0 is the zeroth-order modified Bessel function of the first kind.
The shape parameter β is calculated using
where Astop is the stopband attenuation in dB.
The windowed impulse response is
h(n) for n = 0,1,…,N/2,…,N are the coefficients of the multirate filter. These coefficients are defined by the interpolation factor L and decimation factor M.
OverlapTransition set to
falseThe function designs a lowpass FIR filter with a non-overlapping transition band.
When you set OverlapTransition to
false, the adjusted cutoff frequency
ωc =
2πFc, where
Fc is given by these
equations.
When you specify the polyphase length P,
The filter length N is defined as
where, P is the polyphase length and R is defined by one of these equations:
R = L if L > 1
R = M if L = 1.
When you specify the target transition width TW,
The estimated filter length is given by,
The function adjusts the filter length until the design meets the filter specifications.
The function designs using the equiripple method only if you set
OverlapTransition to false.
When you specify the polyphase length P, the function designs
the filter using the firceqrip function.
num = L*firceqrip(N-1,Fst,[Wp Ws],'stopedge')L is the interpolation factor
R = L if L > 1
R = M if L = 1.
Fst = 1/max(L,M) is the stopband edge frequency
Wp is the passband ripple in linear units
Ws is the stopband attenuation in linear units
When you specify the transition width TW, the function designs
the filter using the firpm function. First, the
function estimates the minimum order filter which meets the peak ripple using the
firpmord function. Then, the
function iteratively calls the firpm function until the measured
stopband ripple is less than the target stopband attenuation that you
specify.
The "lagrange" method uses Lagrange's polynomial interpolation
formula to construct the filter.
The function derives the FIR filter coefficients from Lagrange interpolation
polynomials of order 0 (zero-order hold) and 1 (linear interpolation). Set
PolyphaseLength to 1 for zero-order hold (ZOH)
interpolation, and set PolyphaseLength to 2 for linear
interpolation. The function determines the number of polyphase branches based on the
rate conversion factors L and M.
This MATLAB code shows how the function designs the filter when you set
DesignMethod to "lagrange".
if L>1 R = L; else R = M; end gain = L/R; if P==1 % ZOH num = gain*ones(1,P*R); elseif P==2 % Linear num = gain*triang(1,P*R-1)'; end
In this code,
L is the interpolation factor
M is the decimation factor
P is the polyphase length
R is the number of polyphase branches
num is the vector of filter coefficients
This table shows the filter length N for each combination of conversion factors L and M and the polyphase length P.
| Number of Polyphase Branches (R) | Filter Length (N) | Gain | ||
|---|---|---|---|---|
| ZOH (P=1) | Linear (P=2) | |||
| L = M | 1 | 1 | 1 | 1 |
| L = 1, M > 1 (decimator) | M | M | 2M−1 | 1/M |
| L > 1 (interpolator or sample-rate converter) | L | L | 2L−1 | 1 |
References
[1] Orfanidis, Sophocles J. Introduction to Signal Processing. Upper Saddle River, NJ: Prentice-Hall, 1996.
Extended Capabilities
When you design the filter using the PolyphaseLength
argument, and you set the SystemObject argument to
false, the function supports code generation with no
limitations.
When you design the filter using the TransitionWidth
argument, the inputs to the function must be constants when generating code.
% Transition width equals 0.1 codegen functionName -args {coder.Constant(13),coder.Constant(5),coder.Constant(0.1),coder.Constant(80)} functionName_mex(13,5,0.1,80)
function [B3] = functionName(L,M,TW,Ast) B3 = designMultirateFIR(InterpolationFactor=L,... DecimationFactor=M,... TransitionWidth=TW,... StopbandAttenuation=Ast); end
When you set the
SystemObject argument to true, the
inputs to the function must be constants when generating code. (since R2024a)
This function supports strict single
precision in generated code. If any of the input arguments are in single precision,
or you use the Datatype and
like arguments to specify single-precision (since R2024b),
the code you generate uses strictly single-precision arithmetic. (since R2024a)
Version History
Introduced in R2016aYou can now specify the input sample rate as a positive scalar in Hz using the
InputSampleRate property. The transition width is in Hz and
must be a scalar less than or equal to
InputSampleRate/2.
When you specify InputSampleRate as a positive scalar in Hz
while designing the filter with the designMultirateFIR
function, filter analysis tools such as the filterAnalyzer analyze the filter in Hz instead of in normalized
frequency units. For an example, see Design Kaiser-Window-Based FIR Rate Converter with Nonoverlapping Transition Bands.
You can now specify the design method as "lagrange" in the
designMultirateFIR function. The function designs the FIR
filter based on Lagrange's polynomial interpolation formula. If you set the
polyphase length to 1, the function uses the zero-order hold method, and if you set
the polyphase length to 2, the function uses the linear interpolation method.
For more information, see Algorithms.
For an example that uses this design method, see Design FIR Interpolator Using Lagrange Design Method.
When you set the SystemObject flag to
true, the function now factors out the GCD in the rate conversion
ratio L:M. For example, the function treats an
L:M ratio of 8:4 as 2:1. With this change,
these two function calls have the same
output.
designMultirateFIR(InterpolationFactor=12,DecimationFactor=40,... SystemObject=true) designMultirateFIR(InterpolationFactor=3,DecimationFactor=10,... SystemObject=true)
You can now specify the data type of filter coefficients explicitly using the
Datatype and like arguments.
The designMultirateFIR function now supports the equiripple
design method and non-overlapping transition bands using the new
DesignMethod, OverlapTransition, and
PassbandRipple properties.
Starting in R2024a, specifying the arguments using the Value
only syntax is discouraged in the designMultirateFIR
function.
Existing instances of the function using the Value only
arguments continue to run but are discouraged. Instead, specify the arguments using
the Name=Value syntax.
Starting in R2024a, the designMultirateFIR function supports
specifying the input arguments using the Name=Value
syntax.
Here is the table that shows how to replace your existing code.
| Existing code | Replace with |
|---|---|
designMultirateFIR(L,M) | designMultirateFIR(InterpolationFactor=L,
DecimationFactor=M) |
HP is half-polyphase length and is a positive integer | designMultirateFIR(InterpolationFactor=L,
DecimationFactor=M,
PolyphaseLength=2HP) |
HP is half-polyphase length and is a positive integer. | designMultirateFIR(InterpolationFactor=L,
DecimationFactor=M,
PolyphaseLength=2HP,
StopbandAttenuation=ast) |
TW is transition width and its value is in the range (0, 1). | designMultirateFIR(InterpolationFactor=L,
DecimationFactor=M,
TransitionWidth=TW) |
TW is transition width and its value is in the range (0, 1). | designMultirateFIR(InterpolationFactor=L,
DecimationFactor=M,
TransitionWidth=TW,
StopbandAttenuation=ast) |
The half-polyphase length P input argument is discouraged in
the designMultirateFIR function. Use the
new PolyphaseLength argument instead to specify the polyphase
length 2P.
Existing instances of the function using the half-polyphase length continue to
run. But it is recommended that you replace this code to use the
PolyphaseLength argument.
Here is the table that shows how to replace your existing code.
| Existing code | Replace with |
|---|---|
HP is half-polyphase length and is a positive integer | designMultirateFIR(InterpolationFactor=L,
DecimationFactor=M,
PolyphaseLength=2HP) |
HP is half-polyphase length and is a positive integer. | designMultirateFIR(InterpolationFactor=L,
DecimationFactor=M,
PolyphaseLength=2HP,
StopbandAttenuation=ast) |
When you specify any of the input arguments in single-precision, the
designMultirateFIR function designs filter coefficients in
single precision both in simulation and in generated code.
The designMultirateFIR function supports code generation when
you set the 'SystemObject' flag to
true.
See Also
Functions
designRateConverter|designLowpassFIR|designHighpassFIR|designHalfbandFIR|firnyquist|rcosdesign|fdesign.decimator|fdesign.interpolator|fdesign.halfband|designMultistageDecimator|designFracDelayFIR
Objects
MATLAB Command
You clicked a link that corresponds to this MATLAB command:
Run the command by entering it in the MATLAB Command Window. Web browsers do not support MATLAB commands.
Web サイトの選択
Web サイトを選択すると、翻訳されたコンテンツにアクセスし、地域のイベントやサービスを確認できます。現在の位置情報に基づき、次のサイトの選択を推奨します:
また、以下のリストから Web サイトを選択することもできます。
最適なサイトパフォーマンスの取得方法
中国のサイト (中国語または英語) を選択することで、最適なサイトパフォーマンスが得られます。その他の国の MathWorks のサイトは、お客様の地域からのアクセスが最適化されていません。
南北アメリカ
- América Latina (Español)
- Canada (English)
- United States (English)
ヨーロッパ
- Belgium (English)
- Denmark (English)
- Deutschland (Deutsch)
- España (Español)
- Finland (English)
- France (Français)
- Ireland (English)
- Italia (Italiano)
- Luxembourg (English)
- Netherlands (English)
- Norway (English)
- Österreich (Deutsch)
- Portugal (English)
- Sweden (English)
- Switzerland
- United Kingdom (English)